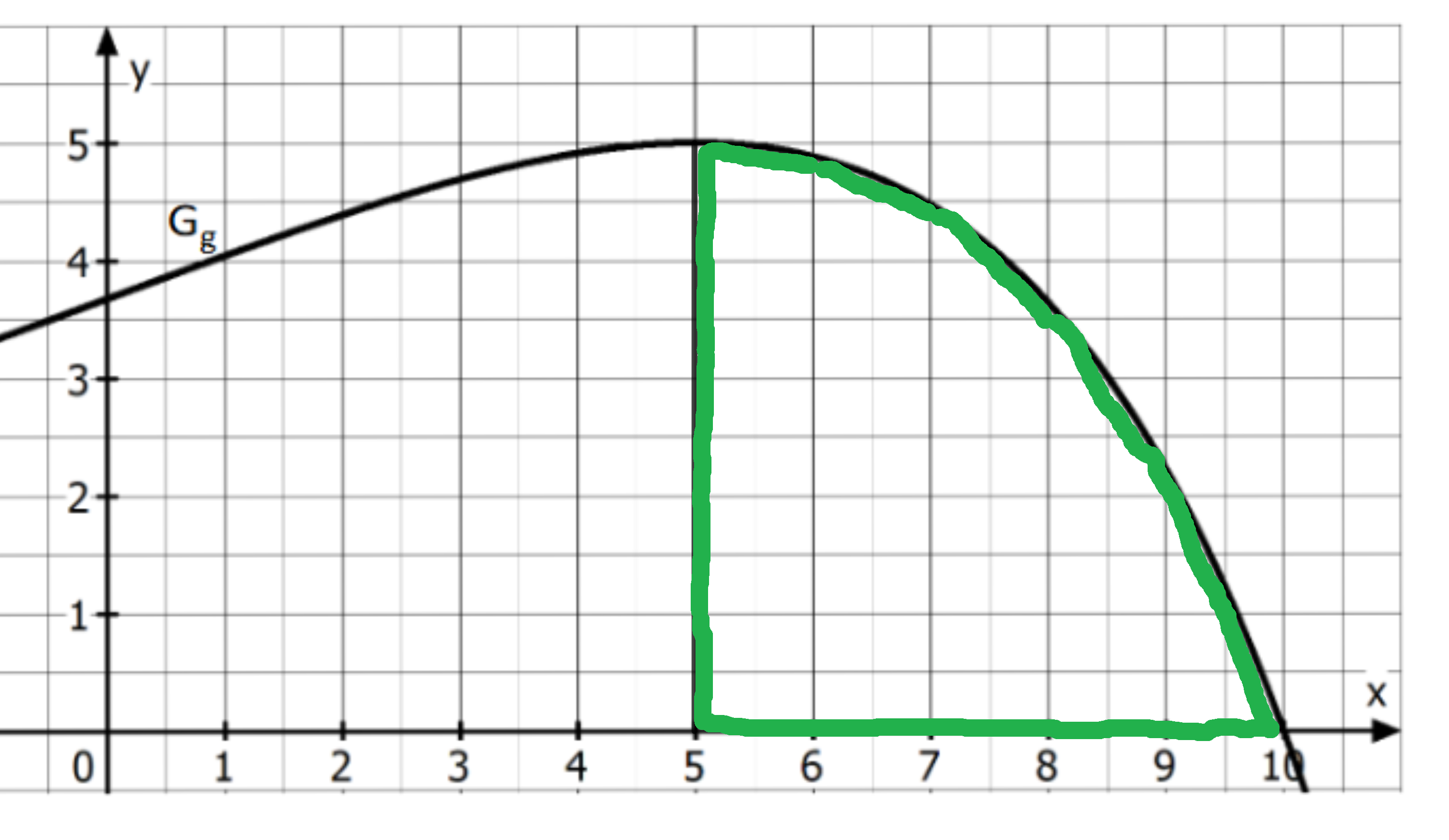
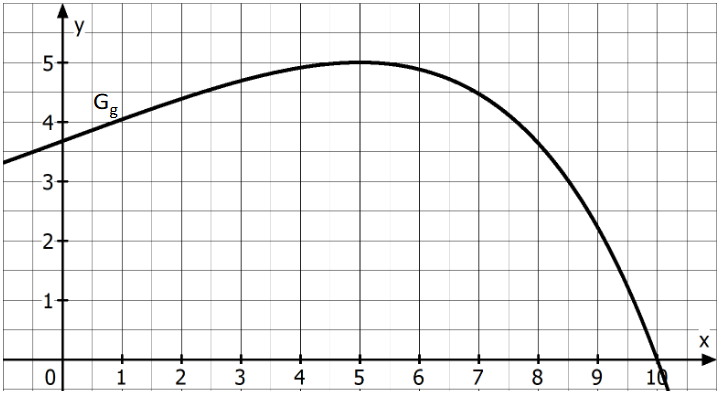
Unten abgebildet ist ein Ausschnitt des Graphen der Funktion mit der maximalen Definitionsmenge .
Geben Sie jeweils an, ob die folgenden Terme Werte haben, die größer, kleiner oder gleich Null sind:
a) b)
(2 BE)
Bestimmen Sie anhand der Abbildung graphisch die Steigung der Tangente an im Punkt . Veranschaulichen Sie Ihr Vorgehen in obiger Abbildung durch ein geeignetes Steigungsdreieck. (3 BE)
Die Funktion ist durch die Gleichung gegeben. Weisen Sie nach, dass die Funktion mit eine Stammfunktion von ist. (3 BE)
Berechnen Sie die ungerundeten Funktionswerte und . Markieren Sie in der Abbildung aus a) das Flächenstück, dessen Flächenmaßzahl gleich der Differenz ist und geben Sie die Maßzahl exakt an. (3 BE)