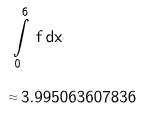B1 - lernen mit Serlo!

Aufgabe 2

Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.

Gegeben ist die Funktion $f$ mit der Gleichung $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x}, x \in ℝ$ .

Der Graph der Funktion $f$ ist in Abbildung 1 dargestellt.

Der Graph der Funktion $f$ , die $x$ -Achse und die Gerade mit der Gleichung $x = 6$ schließen die Fläche $A$ ein.
Ermitteln Sie den Inhalt der Fläche $A$ . (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Ermittele den Inhalt der Fläche $A$
Demnach ist: $A = \int_{0}^{6} f (x) d x \approx 4$ .
Der Inhalt der Fläche $A$ beträgt rund $4 FE$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $A = \int_{0}^{6} f (x) d x$ .
Für jedes $0 < u \leq 6$ sind $O (0 | 0), P (6 | 0)$ und $Q_{u} (u | f (u))$ die Eckpunkte eines Dreiecks.
(i) Zeichnen Sie das Dreieck $O P Q_{u}$ mit $u = 2$ in Abbildung 1 ein. (1 P)
(ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks $O P Q_{u}$ in Abhängigkeit von $u$ mit der Gleichung $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ berechnen lässt. (2 P)
(iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $O P Q_{u}$ maximal wird. (2 P)
(iv) Bestimmen Sie alle Werte von $u$ , für die das Dreieck $O P Q_{u}$ einen Flächeninhalt von 4 Flächeneinheiten hat. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
(i) Zeichne das Dreieck $O P Q_{u}$ mit $u = 2$ in Abbildung 1 ein
Abbildung 1
(ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks $O P Q_{u}$ in Abhängigkeit von $u$ mit der Gleichung $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ berechnen lässt
Da die Grundseite $O P$ des Dreiecks $O P Q_{u}$ eine Länge von $6$ Längeneinheiten hat und die Länge der zugehörigen Höhe durch $f (u)$ gegeben ist, gilt für den Flächeninhalt des Dreiecks $A_{O P Q_{u}} (u) = \frac{1}{2} \cdot 6 \cdot f (u) = 3 \cdot f (u)$ .
(iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $O P Q_{u}$ maximal wird
Bekannt ist: $H P (\frac{2}{3} | \frac{6}{3})$ .
Da der Flächeninhalt immer der dreifache Wert des Funktionswertes $f (u)$ und der Funktionswert im Hochpunkt maximal ist, wird der Flächeninhalt des Dreiecks $O P Q_{u}$ für $u = \frac{2}{3}$ maximal.
(iv) Bestimmen Sie alle Werte von $u$ , für die das Dreieck $O P Q_{u}$ einen Flächeninhalt von 4 Flächeneinheiten hat
Gegeben ist $A_{O P Q_{u}} (u) = 3 \cdot f (u) = 3 \cdot 9 \cdot u \cdot e^{- 1,5 \cdot u} = 27 \cdot u \cdot e^{- 1,5 \cdot u}$ .
Löse die Gleichung $27 \cdot u \cdot e^{- 1,5 \cdot u} = 4$
Somit ist $u \approx 0,20 \lor u \approx 1,58$ .
Für diese beiden Werte hat das Dreieck $O P Q_{u}$ einen Flächeninhalt von $4$ Flächeneinheiten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
(i)
Zeichne die drei gegebenen Punkte in die Abbildung ein und verbinde sie zu einem Dreieck.
(ii)
Die Grundseite des Dreiecks hat immer die Länge $6$ und die zugehörige Höhe ist durch $f (u)$ gegeben. Setze in die Dreiecksflächenformel ein.
(iii)
Wenn $Q_{u}$ im Hochpunkt des Graphen von $f$ liegt, ist die Dreiecksfläche maximal.
(iv)
Es ist $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ .
Setze $f (u)$ ein und löse die Gleichung $A_{O P Q_{u}} (u) = 4$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 2

Ermittele den Inhalt der Fläche A

Hast du eine Frage oder Feedback?

(i) Zeichne das Dreieck OPQu mit u=2 in Abbildung 1 ein

(ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks OPQu in Abhängigkeit von u mit der Gleichung AOPQu(u)=3⋅f(u) berechnen lässt

(iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von u der Flächeninhalt des Dreiecks OPQu maximal wird

(iv) Bestimmen Sie alle Werte von u, für die das Dreieck OPQu einen Flächeninhalt von 4 Flächeneinheiten hat

Hast du eine Frage oder Feedback?

Ermittele den Inhalt der Fläche $A$

(i) Zeichne das Dreieck $O P Q_{u}$ mit $u = 2$ in Abbildung 1 ein

(ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks $O P Q_{u}$ in Abhängigkeit von $u$ mit der Gleichung $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ berechnen lässt

(iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $O P Q_{u}$ maximal wird

(iv) Bestimmen Sie alle Werte von $u$ , für die das Dreieck $O P Q_{u}$ einen Flächeninhalt von 4 Flächeneinheiten hat