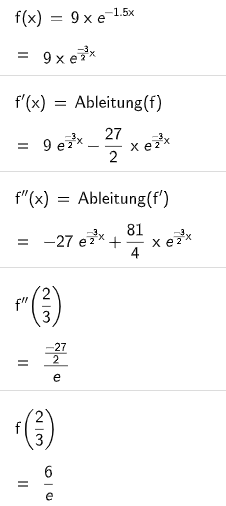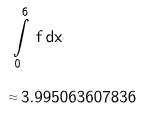B1

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben ist die Funktion $f$ mit der Gleichung $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x}, x \in ℝ$ .
Der Graph der Funktion $f$ ist in Abbildung 1 dargestellt.
Abbildung 1
1. Begründen Sie, dass die Funktion $f$ nur eine Nullstelle besitzt. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Begründe, dass die Funktion $f$ nur eine Nullstelle besitzt
  Es ist $e^{- 1,5 \cdot x} > 0$ für alle $x \in ℝ$ .
  Deshalb gilt: $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x} = 0 \Leftrightarrow x = 0$ .
  Somit besitzt die Funktion $f$ nur eine Nullstelle an der Stelle $x = 0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $e^{- 1,5 \cdot x} > 0$ für alle $x \in ℝ$ . $f (x)$ kann nur für $x = 0$ null werden.
2. Untersuchen Sie den Graphen von $f$ rechnerisch auf lokale Extrempunkte. (5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Untersuche den Graphen von $f$ rechnerisch auf lokale Extrempunkte
  Berechne $f^{'} (x)$ und $f^{''} (x)$ :
  Der CAS Rechner liefert $f^{'} (x) = (9 - \frac{27}{2} x) \cdot e^{- 1,5 \cdot x}$ und $f^{''} (x) = (\frac{81}{4} \cdot x - 27) \cdot e^{- 1,5 \cdot x}$ .
  Die notwendige Bedingung für einen Extrempunkt ist $f^{'} (x) = 0$ .
  Setze $f^{'} (x) = 0 \Rightarrow 9 - \frac{27}{2} x = 0 \Rightarrow x = \frac{2}{3}$ .
  An der Stelle $x = \frac{2}{3}$ liegt eine Extremstelle vor.
  Überprüfe die Art der Extremstelle mit der 2. Ableitung:
  $f^{''} (\frac{2}{3}) = - \frac{27}{2} \cdot e^{- 1} < 0$
  Der Graph der Funktion $f$ hat an der Stelle $x = \frac{2}{3}$ einen Hochpunkt.
  Berechne $f (\frac{2}{3}) = \frac{6}{e} \approx 2,21$ $\Rightarrow H P (\frac{2}{3} | \frac{6}{e})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f^{'} (x)$ und $f^{''} (x)$ .
  Die notwendige Bedingung für einen Extrempunkt ist $f^{'} (x) = 0$ .
  Setze $f^{'} (x) = 0 \Rightarrow x_{1}$ .
  Bestimme die Art des Extremums mit $f^{''} (x_{1})$ .
  Berechne $f (x_{1}) \Rightarrow E (x_{1} | f (x_{1}))$ .
3. Der Graph der Funktion $f$ hat genau einen Wendepunkt.
  Ermitteln Sie die Koordinaten des Wendepunktes. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Ermittele die Koordinaten des Wendepunktes
  Es ist $f^{''} (x) = (\frac{81}{4} \cdot x - 27) \cdot e^{- 1,5 \cdot x}$
  Die notwendige Bedingung für einen Wendepunkt ist $f^{''} (x) = 0$ .
  $\Rightarrow 0 = \frac{81}{4} \cdot x - 27 \Rightarrow x = \frac{4}{3}$
  Laut Aufgabenstellung hat der Graph von $f$ genau einen Wendepunkt und der liegt an der Stelle $x = \frac{4}{3}$ vor.
  Berechne $f (\frac{4}{3}) = 9 \cdot \frac{4}{3} \cdot e^{- \frac{3}{2} \cdot \frac{4}{3}} = 12 \cdot e^{- 2}$ .
  Somit hat der Wendepunkt die Koordinaten $W P (\frac{4}{3} | 12 \cdot e^{- 2})$ , gerundet $W P (1,33 | 1,62)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Laut Aufgabenstellung hat der Graph von $f$ genau einen Wendepunkt.
  Die notwendige Bedingung für einen Wendepunkt ist $f^{''} (x) = 0$ .
  Löse diese Gleichung nach $x_{W}$ auf und berechne $f (x_{W})$ .
4. Ermitteln Sie, an welchen Stellen im Intervall $[0; 6]$ der Graph der Funktion $f$ die größte bzw. die kleinste Steigung hat. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
  Ermittele, an welchen Stellen im Intervall $[0; 6]$ der Graph der Funktion $f$ die größte bzw. die kleinste Steigung hat
  Die größte bzw. kleinste Steigung liegt im Wendepunkt oder am Rand des Intervalls vor.
  Berechne $f^{'} (0), f^{'} (\frac{4}{3})$ und $f^{'} (6)$ :
  Es ist $f^{'} (x) = (9 - \frac{27}{2} x) \cdot e^{- 1,5 \cdot x}$ .
  Dann folgt:
  $f^{'} (0) = 9$
  $f^{'} (\frac{4}{3}) = (9 - \frac{27}{2} \cdot \frac{4}{3}) \cdot e^{- \frac{3}{2} \cdot \frac{4}{3}} = - 9 \cdot e^{- 2} \approx - 1,22$
  $f^{'} (6) = (9 - \frac{27}{2} \cdot 6) \cdot e^{- \frac{3}{2} \cdot 6} = - 72 \cdot e^{- 9} \approx - 0,01$
  Die größte Steigung besteht an der Stelle $x = 0$ und die kleinste Steigung liegt an der Wendestelle $x = \frac{4}{3}$ vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f^{'} (0), f^{'} (\frac{4}{3})$ und $f^{'} (6)$ und vergleiche.
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist die Funktion $f$ mit der Gleichung $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x}, x \in ℝ$ .
Der Graph der Funktion $f$ ist in Abbildung 1 dargestellt.
Abbildung 1
1. Der Graph der Funktion $f$ , die $x$ -Achse und die Gerade mit der Gleichung $x = 6$ schließen die Fläche $A$ ein.
  Ermitteln Sie den Inhalt der Fläche $A$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Ermittele den Inhalt der Fläche $A$
  Demnach ist: $A = \int_{0}^{6} f (x) d x \approx 4$ .
  Der Inhalt der Fläche $A$ beträgt rund $4 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $A = \int_{0}^{6} f (x) d x$ .
2. Für jedes $0 < u \leq 6$ sind $O (0 | 0), P (6 | 0)$ und $Q_{u} (u | f (u))$ die Eckpunkte eines Dreiecks.
  (i) Zeichnen Sie das Dreieck $O P Q_{u}$ mit $u = 2$ in Abbildung 1 ein. (1 P)
  (ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks $O P Q_{u}$ in Abhängigkeit von $u$ mit der Gleichung $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ berechnen lässt. (2 P)
  (iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $O P Q_{u}$ maximal wird. (2 P)
  (iv) Bestimmen Sie alle Werte von $u$ , für die das Dreieck $O P Q_{u}$ einen Flächeninhalt von 4 Flächeneinheiten hat. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  (i) Zeichne das Dreieck $O P Q_{u}$ mit $u = 2$ in Abbildung 1 ein
  Abbildung 1
  (ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks $O P Q_{u}$ in Abhängigkeit von $u$ mit der Gleichung $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ berechnen lässt
  Da die Grundseite $O P$ des Dreiecks $O P Q_{u}$ eine Länge von $6$ Längeneinheiten hat und die Länge der zugehörigen Höhe durch $f (u)$ gegeben ist, gilt für den Flächeninhalt des Dreiecks $A_{O P Q_{u}} (u) = \frac{1}{2} \cdot 6 \cdot f (u) = 3 \cdot f (u)$ .
  (iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $O P Q_{u}$ maximal wird
  Bekannt ist: $H P (\frac{2}{3} | \frac{6}{3})$ .
  Da der Flächeninhalt immer der dreifache Wert des Funktionswertes $f (u)$ und der Funktionswert im Hochpunkt maximal ist, wird der Flächeninhalt des Dreiecks $O P Q_{u}$ für $u = \frac{2}{3}$ maximal.
  (iv) Bestimmen Sie alle Werte von $u$ , für die das Dreieck $O P Q_{u}$ einen Flächeninhalt von 4 Flächeneinheiten hat
  Gegeben ist $A_{O P Q_{u}} (u) = 3 \cdot f (u) = 3 \cdot 9 \cdot u \cdot e^{- 1,5 \cdot u} = 27 \cdot u \cdot e^{- 1,5 \cdot u}$ .
  Löse die Gleichung $27 \cdot u \cdot e^{- 1,5 \cdot u} = 4$
  Somit ist $u \approx 0,20 \lor u \approx 1,58$ .
  Für diese beiden Werte hat das Dreieck $O P Q_{u}$ einen Flächeninhalt von $4$ Flächeneinheiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Zeichne die drei gegebenen Punkte in die Abbildung ein und verbinde sie zu einem Dreieck.
  (ii)
  Die Grundseite des Dreiecks hat immer die Länge $6$ und die zugehörige Höhe ist durch $f (u)$ gegeben. Setze in die Dreiecksflächenformel ein.
  (iii)
  Wenn $Q_{u}$ im Hochpunkt des Graphen von $f$ liegt, ist die Dreiecksfläche maximal.
  (iv)
  Es ist $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ .
  Setze $f (u)$ ein und löse die Gleichung $A_{O P Q_{u}} (u) = 4$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist die Funktion $f$ mit der Gleichung $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x}, x \in ℝ$ .
Für ein $z$ mit $\frac{2}{3} < z < \frac{4}{3}$ ist der Punkt $R (z | f (z))$ gegeben. Der Graph der Funktion $t$ ist die Tangente an den Graphen von $f$ im Punkt $R$ . Für $x < z$ wird der Graph von $f$ betrachtet. Für $x \geq z$ wird der Graph von $t$ betrachtet. Abbildung 2 veranschaulicht diese Situation für das Beispiel $z = 0,9$ .
Die betrachteten Graphen der Funktionen $f$ und $t$ schließen mit der $x$ -Achse die in Abbildung 2 schraffiert dargestellte Fläche ein. Der Wert von $z$ kann mithilfe der folgenden Bedingungen so bestimmt werden, dass diese Fläche einen Flächeninhalt von 4 Flächeneinheiten hat:
I: $t (z) = f (z)$
II: $t^{'} (z) = f^{'} (z)$
III: $\int_{0}^{z} f (x) d x + \int_{z}^{c} t (x) d x = 4$ , wobei $c$ die Nullstelle von $t$ ist.
Abbildung 2
1. (i) Begründen Sie die Wahl der Bedingungen I und II. (2 P)
  (ii) Erläutern Sie die linke Seite der Gleichung in Bedingung III. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  (i) Begründe die Wahl der Bedingungen I und II
  Die Bedingungen I und II stellen sicher, dass es sich bei der Funktion $t$ um die Tangente an den Graphen der Funktion $f$ im Punkt $R$ handelt bzw. dass der Übergang „knickfrei“ erfolgt.
  (ii) Erläutere die linke Seite der Gleichung in Bedingung III
  Mit dem ersten Integral wird der Inhalt der Fläche zwischen dem Graphen von $f$ und der $x$ -Achse über dem Intervall $[0; z]$ berechnet.
  Mit dem zweiten Integral wird der Inhalt der Fläche zwischen dem Graphen von $t$ und der $x$ -Achse über dem Intervall $[z; c]$ berechnet, wobei $c$ die Nullstelle der Funktion $t$ ist.
  Die Addition der beiden Integrale ergibt den Flächeninhalt der in der Aufgabe beschriebenen Fläche.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Welche Bedingungen müssen erfüllt sein, damit $t$ Tangente an f ist?
  Welche Bedingungen müssen erfüllt sein, damit der Übergang zwischen $f$ und $t$ „knickfrei“ erfolgt?
  (ii)
  Es werden zwei Flächen berechnet.
  Um welche Flächen handelt es sich?
  Wie groß ist die Gesamtfläche?
2. Aus den Bedingungen folgt $z \approx 0,9428$ . [Nachweis nicht erforderlich.]
  (i) Bestimmen Sie für $z = 0,9428$ rechnerisch eine Gleichung der Funktion $t$ , deren Graph die Tangente an den Graphen von $f$ im Punkt $R (z | f (z))$ ist. (3 P)
  (ii) Ermitteln Sie die Nullstelle dieser Funktion $t$ . (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  (i) Bestimme für $z = 0,9428$ rechnerisch eine Gleichung der Funktion $t$ , deren Graph die Tangente an den Graphen von $f$ im Punkt $R (z | f (z))$ ist
  Gegeben ist $z = 0,9428$ .
  Dann ist $f^{'} (0,9428) \approx - 0,9063$ und $f (0,9428) \approx 2,0629$ .
  Für die allgemeine Tangentengleichung gilt:
  $y = f^{'} (z) \cdot (x - z) + f (z)$
  Die Funktion $t$ hat somit die Gleichung (gerundete Werte):
  $t (x) = - 0,9063 \cdot (x - 0,9428) + 2,0629 \approx - 0,9063 \cdot x + 2,9174$
  Die Gleichung der Funktion $t$ , deren Graph die Tangente an den Graphen von $f$ im Punkt $R (0,9428 | f (0,9428))$ ist, lautet $t (x) = - 0,9063 \cdot x + 2,9174$ .
  (ii) Ermittele die Nullstelle dieser Funktion
  Setze $t (x) = 0$ :
  $0 = - 0,9063 \cdot x + 2,9174 \Rightarrow x = \frac{2,9174}{0,9063} \approx 3,22$
  Die Nullstelle dieser Funktion ist $x \approx 3,22$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Gegeben ist $z = 0,9428$ .
  Berechne $f^{'} (z)$ und $f (z)$ .
  Setze in $t : y = f^{'} (z) \cdot (x - z) + f (z)$ ein.
  (ii)
  Setze $t (x) = 0$ und löse nach $x$ auf.
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist die Funktion $f$ mit der Gleichung $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x}, x \in ℝ$ .
Für $k > 0$ ist die Funktion $j$ mit der Gleichung $j (x) = 4 \cdot k^{2} \cdot x \cdot e^{- k \cdot x}$ für $x \in ℝ$ gegeben.
Setzt man $k = 1,5$ in den Funktionsterm von $j$ ein, so erhält man den Funktionsterm von $f$ .
Setzt man $k = 2,6$ in den Funktionsterm von $j$ ein, so erhält man den Funktionsterm der Funktion $g$ mit $g (x) = 4 \cdot {2,6}^{2} \cdot x \cdot e^{- 2,6 \cdot x}$ .
Abbildung 3
1. Die Graphen der Funktionen $f$ und $g$ schneiden sich nur im Koordinatenursprung und in einem weiteren Punkt $S$ .
  (i) Bestimmen Sie die Koordinaten des Hochpunkts des Graphen von $g$ und des Schnittpunkts $S$ der Graphen von $f$ und $g$ . (2 P)
  (ii) Skizzieren Sie mithilfe dieser Punkte den Graphen der Funktion $g$ in Abbildung 3.
  (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  (i) Bestimme die Koordinaten des Hochpunkts des Graphen von $g$ und des Schnittpunkts $S$ der Graphen von $f$ und g
  Gegeben sind $f (x) = 9 \cdot x \cdot e^{- 1,5 \cdot x}$ und $g (x) = 4 \cdot {2,6}^{2} \cdot x \cdot e^{- 2,6 \cdot x} = 27,04 \cdot x \cdot e^{- 2,6 \cdot x}$ .
  Betrachte die Graphen der beiden Funktionen. Für den Hochpunkt des Graphen von $g$ erhält man $x_{H} \approx 0,3846$ und $y_{H} \approx 3,8259$ , sodass sich gerundet der Hochpunkt ergibt: $H P (0,38 | 3,83)$ .
  Für den Schnittpunkt $S$ der Graphen von $f$ und g erhält man $x_{S} \approx 1,000084$ und $y_{S} \approx 2,008087$ , sodass sich gerundet der Schnittpunkt $S$ ergibt: $S (1 | 2)$ .
  (ii) Skizziere mithilfe dieser Punkte den Graphen der Funktion $g$ in Abbildung 3
  Abbildung 3
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Graphen der beiden Funktionen $f$ und $g$ und lasse Dir den Hochpunkt von $g$ und den zweiten Schnittpunkt $S$ anzeigen.
2. Setzt man einen bestimmten Wert von $k$ in den Funktionsterm von $j$ ein, so erhält man den Funktionsterm der Funktion $h$ , deren Graph in Abbildung 3 dargestellt ist.
  Geben Sie ohne weitere Rechnung einen Schätzwert für diesen Wert von $k$ an. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Gib ohne weitere Rechnung einen Schätzwert für diesen Wert von $k$ an
  Für $k = 1,5$ erhält man die Funktion $f$ .
  Für $k = 2,6$ erhält man die Funktion $g$ .
  Der Graph der Funktion $h$ liegt zwischen den beiden Graphen von $f$ und $g$ , sodass hier $k \approx 2$ sein muss.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für $k = 1,5$ erhält man die Funktion $f$ . Für $k = 2,6$ erhält man die Funktion $g$ .
  Der Graph der Funktion $h$ liegt zwischen den beiden Graphen von $f$ und $g$ .
  Welchen Wert kann man dann für $k$ annehmen?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B1

Aufgabe 1

Begründe, dass die Funktion f nur eine Nullstelle besitzt

Hast du eine Frage oder Feedback?

Untersuche den Graphen von f rechnerisch auf lokale Extrempunkte

Hast du eine Frage oder Feedback?

Ermittele die Koordinaten des Wendepunktes

Hast du eine Frage oder Feedback?

Ermittele, an welchen Stellen im Intervall [0;6] der Graph der Funktion f die größte bzw. die kleinste Steigung hat

Hast du eine Frage oder Feedback?

Aufgabe 2

Ermittele den Inhalt der Fläche A

Hast du eine Frage oder Feedback?

(i) Zeichne das Dreieck OPQu mit u=2 in Abbildung 1 ein

(ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks OPQu in Abhängigkeit von u mit der Gleichung AOPQu(u)=3⋅f(u) berechnen lässt

(iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von u der Flächeninhalt des Dreiecks OPQu maximal wird

(iv) Bestimmen Sie alle Werte von u, für die das Dreieck OPQu einen Flächeninhalt von 4 Flächeneinheiten hat

Hast du eine Frage oder Feedback?

Aufgabe 3

(i) Begründe die Wahl der Bedingungen I und II

(ii) Erläutere die linke Seite der Gleichung in Bedingung III

Hast du eine Frage oder Feedback?

(i) Bestimme für z=0,9428 rechnerisch eine Gleichung der Funktion t, deren Graph die Tangente an den Graphen von f im Punkt R(z|f(z)) ist

(ii) Ermittele die Nullstelle dieser Funktion

Hast du eine Frage oder Feedback?

Aufgabe 4

(i) Bestimme die Koordinaten des Hochpunkts des Graphen von g und des Schnittpunkts S der Graphen von f und g

(ii) Skizziere mithilfe dieser Punkte den Graphen der Funktion g in Abbildung 3

Hast du eine Frage oder Feedback?

Gib ohne weitere Rechnung einen Schätzwert für diesen Wert von k an

Hast du eine Frage oder Feedback?

Begründe, dass die Funktion $f$ nur eine Nullstelle besitzt

Untersuche den Graphen von $f$ rechnerisch auf lokale Extrempunkte

Ermittele, an welchen Stellen im Intervall $[0; 6]$ der Graph der Funktion $f$ die größte bzw. die kleinste Steigung hat

Ermittele den Inhalt der Fläche $A$

(i) Zeichne das Dreieck $O P Q_{u}$ mit $u = 2$ in Abbildung 1 ein

(ii) Begründen Sie, dass sich der Flächeninhalt des Dreiecks $O P Q_{u}$ in Abhängigkeit von $u$ mit der Gleichung $A_{O P Q_{u}} (u) = 3 \cdot f (u)$ berechnen lässt

(iii) Begründen Sie ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $O P Q_{u}$ maximal wird

(iv) Bestimmen Sie alle Werte von $u$ , für die das Dreieck $O P Q_{u}$ einen Flächeninhalt von 4 Flächeneinheiten hat

(i) Bestimme für $z = 0,9428$ rechnerisch eine Gleichung der Funktion $t$ , deren Graph die Tangente an den Graphen von $f$ im Punkt $R (z | f (z))$ ist

(i) Bestimme die Koordinaten des Hochpunkts des Graphen von $g$ und des Schnittpunkts $S$ der Graphen von $f$ und g

(ii) Skizziere mithilfe dieser Punkte den Graphen der Funktion $g$ in Abbildung 3

Gib ohne weitere Rechnung einen Schätzwert für diesen Wert von $k$ an