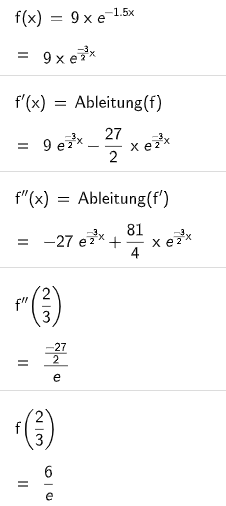Begründe, dass die Funktion $f$ nur eine Nullstelle besitzt

Es ist ${\mathrm{e}}^{-\mathrm{1,5}\cdot x}>0$ für alle $x\in ℝ$.

Deshalb gilt: $f(x)=9\cdot x\cdot {\mathrm{e}}^{-\mathrm{1,5}\cdot x}=0\iff x=0$.

Somit besitzt die Funktion $f$ nur eine Nullstelle an der Stelle $x=0$.

Untersuche den Graphen von $f$ rechnerisch auf lokale Extrempunkte

Berechne $f^{\prime }(x)$ und $f^{\prime \prime }(x)$:

Der CAS Rechner liefert $f^{\prime }(x)=(9-\frac{27}{2}x)\cdot {\mathrm{e}}^{-\mathrm{1,5}\cdot x}$ und $f^{\prime \prime }(x)=(\frac{81}{4}\cdot x-27)\cdot {\mathrm{e}}^{-\mathrm{1,5}\cdot x}$.

Die notwendige Bedingung für einen Extrempunkt ist $f^{\prime }(x)=0$.

Setze $f^{\prime }(x)=0\Rightarrow 9-{\displaystyle \frac{27}{2}}x=0\Rightarrow x={\displaystyle \frac{2}{3}}$.

An der Stelle $x={\displaystyle \frac{2}{3}}$ liegt eine Extremstelle vor.

Überprüfe die Art der Extremstelle mit der 2. Ableitung:

$f^{\prime \prime }\left({\displaystyle \frac{2}{3}}\right)=-{\displaystyle \frac{27}{2}}\cdot e^{-1}<0$

Der Graph der Funktion $f$ hat an der Stelle $x=\frac{2}{3}$ einen Hochpunkt.

Berechne $f(\frac{2}{3})={\displaystyle \frac{6}{e}}\approx \mathrm{2,21}$$\Rightarrow HP\left(\frac{2}{3}|\frac{6}{e}\right)$.

Ermittele die Koordinaten des Wendepunktes

Es ist $f^{\prime \prime }(x)=(\frac{81}{4}\cdot x-27)\cdot {\mathrm{e}}^{-\mathrm{1,5}\cdot x}$

Die notwendige Bedingung für einen Wendepunkt ist $f^{\prime \prime }(x)=0$.

$\Rightarrow 0=\frac{81}{4}\cdot x-27\Rightarrow x={\displaystyle \frac{4}{3}}$

Laut Aufgabenstellung hat der Graph von $f$ genau einen Wendepunkt und der liegt an der Stelle $x={\displaystyle \frac{4}{3}}$ vor.

Berechne $f(\frac{4}{3})=9\cdot {\displaystyle \frac{4}{3}}\cdot e^{-\frac{3}{2}\cdot \frac{4}{3}}=12\cdot e^{-2}$.

Somit hat der Wendepunkt die Koordinaten $WP(\frac{4}{3}|12\cdot e^{-2})$, gerundet $WP(\mathrm{1,33}|\mathrm{1,62})$.

Ermittele, an welchen Stellen im Intervall $[0;6]$ der Graph der Funktion $f$ die größte bzw. die kleinste Steigung hat

Die größte bzw. kleinste Steigung liegt im Wendepunkt oder am Rand des Intervalls vor.

Berechne $f^{\prime }(0),f^{\prime }(\frac{4}{3})$ und $f^{\prime }(6)$:

Es ist $f^{\prime }(x)=(9-\frac{27}{2}x)\cdot {\mathrm{e}}^{-\mathrm{1,5}\cdot x}$.

Dann folgt:

$f^{\prime }(0)=9$

$f^{\prime }(\frac{4}{3})=(9-\frac{27}{2}\cdot \frac{4}{3})\cdot {\mathrm{e}}^{-\frac{3}{2}\cdot \frac{4}{3}}=-9\cdot e^{-2}\approx -\mathrm{1,22}$

$f^{\prime }(6)=(9-\frac{27}{2}\cdot 6)\cdot {\mathrm{e}}^{-\frac{3}{2}\cdot 6}=-72\cdot e^{-9}\approx -\mathrm{0,01}$

Die größte Steigung besteht an der Stelle $x=0$ und die kleinste Steigung liegt an der Wendestelle $x=\frac{4}{3}$ vor.