Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Gegeben sind und .
Der Körper ist Teil eines mathematischen Modells eines Architekturbüros zur Planung eines neuen Hotels. Das Hotel soll zehn Stockwerke gleicher Höhe besitzen. Für die an die Schrägen angrenzenden Hotelzimmer sind von der 1. bis zur 9. Etage Balkone geplant. Als Beispiel ist in Abbildung 2 der Boden des Balkons für die 3. Etage dargestellt.
Eine Längeneinheit im Modell entspricht einem Meter in der Realität.
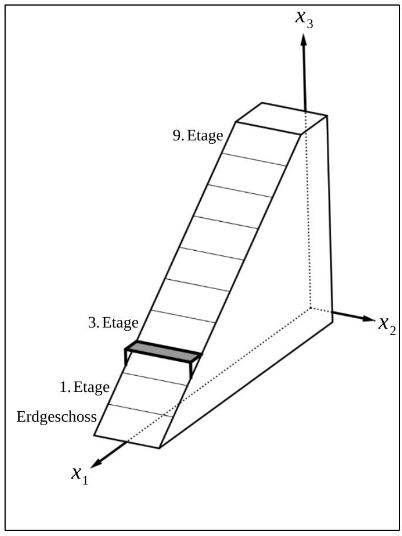
Abbildung 2
Durch , ist eine Schar paralleler Ebenen gegeben. Der Boden jedes Balkons wird im Folgenden als Fläche innerhalb einer geeigneten Ebene der Schar modelliert. Der Boden des Balkons für die 3. Etage liegt z. B. in der Ebene .
Zeigen Sie: Für jeden Wert von a mit liegt der Punkt auf der Strecke . (4 P)
Die Menge aller Punkte der Bodenfläche des Balkons für die 3. Etage wird durch die Parametergleichung
beschrieben.
Der Balkon ist wie in Abbildung 3 dargestellt auf zwei vertikalen Stützen und gelagert.
Berechnen Sie die Länge der Stütze . (4 P)
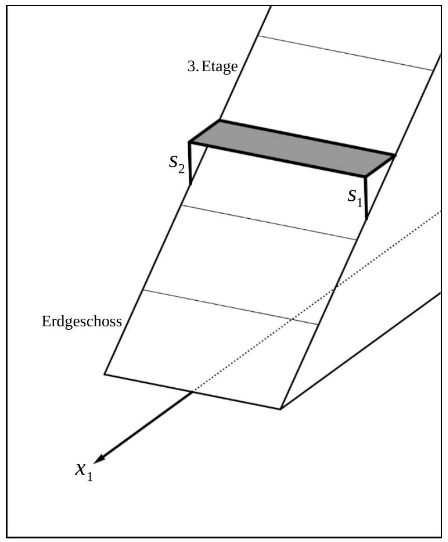
Abbildung 3
