Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für die Funktion mit .
Dabei entspricht eine Längeneinheit im Koordinatensystem in der Realität.
Siehe Abbildung 2:
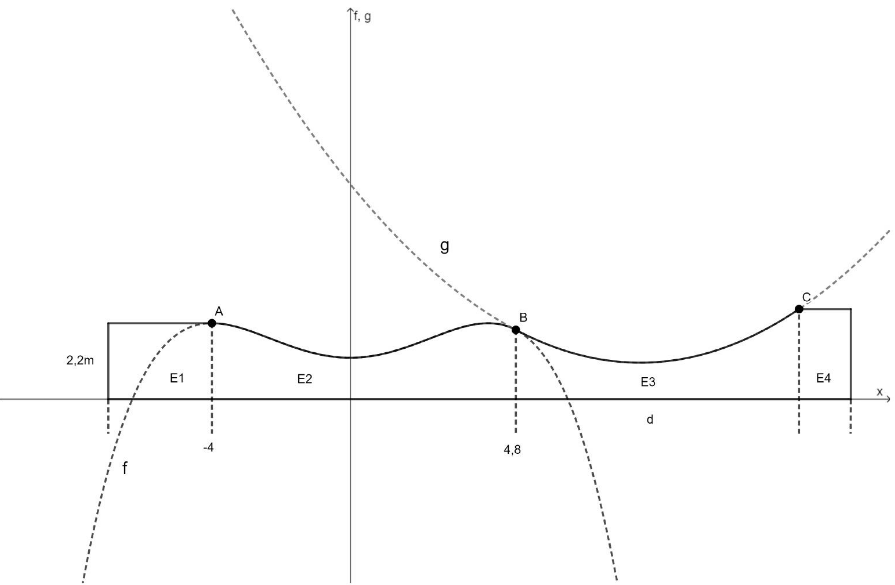
Abbildung 2
Verwenden Sie im Folgenden für die Modellierung von E3 die Gleichung
.
Ein Übergang ist ruckfrei, wenn an der Übergangsstelle neben den Funktionswerten und den ersten Ableitungen auch die zweiten Ableitungen übereinstimmen.
Prüfen Sie, ob es sich beim Übergang von E2 zu E3 um einen ruckfreien Übergang handelt. (2 P)
