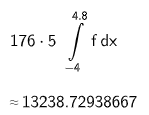B2

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
In einem Skatepark soll ein neuer Teilabschnitt gebaut werden. Der Entwurf des Architekten für den Längsschnitt des Abschnitts ist in Abbildung 1 zu sehen.
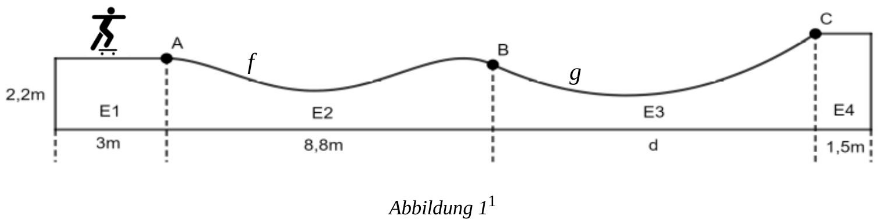
Der Abschnitt soll aus vier Betonelementen mit senkrechten Seitenwänden zusammengesetzt werden. Die äußeren Elemente E1 und E4 sind quaderförmig, für die beiden mittleren Elemente E2 und E3 werden die in Abbildung 1 dargestellten oberen Randlinien durch zwei ganzrationale Funktionen $f$ und $g$ modelliert (Abbildung 2). Die in Abbildung 1 dargestellten unteren Randlinien aller vier Elemente werden durch die $x$ -Achse modelliert.
Außer beim Übergang von E3 zu E4 sollen die dargestellten oberen Randlinien der Elemente „knickfrei“ ineinander übergehen, um ein störungsfreies Fahren zu gewährleisten.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .
Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.
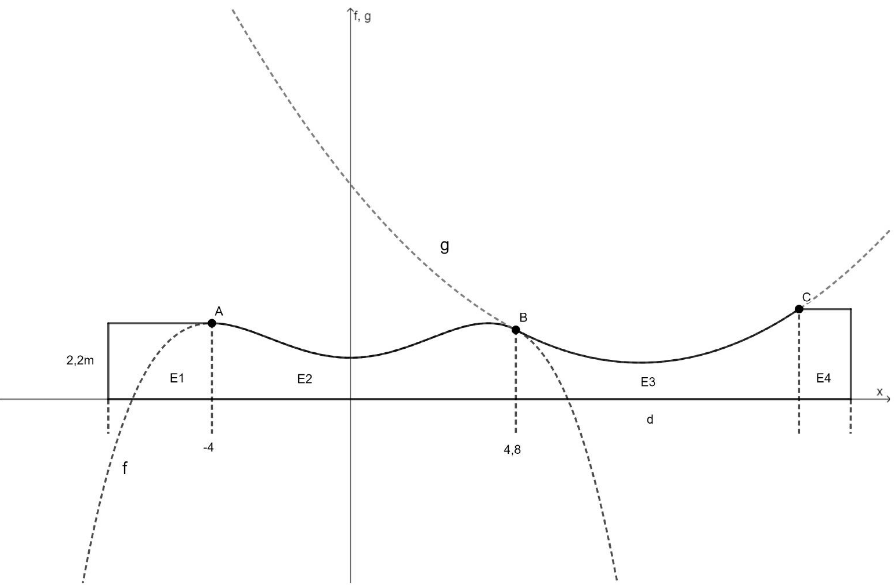
Abbildung 2
1. Begründen Sie, dass $f (x) = f (- x)$ für alle $x \in \mathbb{R}$ gilt, und interpretieren Sie dies geometrisch. (1 P + 1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
  Begründe, dass $f (x) = f (- x)$ für alle $x \in \mathbb{R}$ gilt, und interpretieren Sie dies geometrisch
  Da $f$ eine ganzrationale Funktion mit ausschließlich geraden Exponenten ist, gilt $f (x) = f (- x)$ . Geometrische Interpretation: Der Graph von $f$ ist achsensymmetrisch zur $y$ -Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Funktionsterm von f hat nur gerade Exponenten. Was bedeutet das?
  Welche Symmetrie liegt vor?
2. Ermitteln Sie rechnerisch den Höhenunterschied zwischen dem höchsten und tiefsten Punkt der Skatebahn im Bereich von E2. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Ermittele rechnerisch den Höhenunterschied zwischen dem höchsten und tiefsten Punkt der Skatebahn im Bereich von E2
  Gesucht sind die globalen Extrema von $f$ im Intervall $[- 4; 4,8]$ . Als globale Extremstellen kommen nur die Nullstellen von $f^{'}$ und die Randstellen infrage:
  Wegen $f (- 4) = 2,2 = f (4), f (0) = 1,2$ und $f (4,8) = 2,0064$ liegt das globale Maximum von $f$ im Intervall $[- 4; 4,8$ $]$ bei $2,2$ und das globale Minimum bei $1,2$ .
  Damit gilt:
  Der maximale Höhenunterschied beträgt $f(4)-f(0)=2{,}2 \mathrm{~m}-1{,}2 \mathrm{~m}=1 \mathrm{~m}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gesucht sind die globalen Extrema von $f$ im Intervall $[- 4; 4,8]$ .
  Als globale Extremstellen kommen nur die Nullstellen von $f^{'}$ und die Randstellen infrage.
  Berechne $f^{'} (x)$ und löse die Gleichung $f'(x)=0\;\Rightarrow\;x_1,x_2$ und $x_{3}$ .
  Berechne die Funktionswerte an diesen Stellen und an den Randstellen und vergleiche.
  Die Differenz des größten und kleinsten Wertes ergibt den Höhenunterschied.
3. Zeigen Sie, dass die obere Randlinie von Element E2 knickfrei an die obere Randlinie des quaderförmigen Elements E1 anschließt. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Anwendungsaufgaben der Differential- und Integralrechnung
  Zeigen Sie, dass die obere Randlinie von Element E2 knickfrei an die obere Randlinie des quaderförmigen Elements E1 anschließt
  "Knickfrei" bedeutet, dass an den Verbindungsstellen zweier Funktionen die Funktionswerte und die Steigungen übereinstimmen.
  Nach Aufgabe b) ist $f (- 4) = 2,2$ und $f^{\prime}(-4)=0$ . An der Stelle $x = - 4$ stimmen die oberen Randlinien von E1 und E2 in der Höhe und in der Steigung überein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Prüfe, ob bei $x = - 4$ der Funktionswert $f (- 4)$ gleich der Höhe des quaderförmigen Elements E1 ist und prüfe, ob die Steigungen der beiden Funktionen an dieser Stelle übereinstimmen.
4. Aus Sicherheitsgründen soll an der steilsten Stelle der Bahn der Betrag der Steigung höchstens $0,85$ sein.
  Zeigen Sie, dass diese Vorgabe beim Element E2 eingehalten wird. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Zeige, dass diese Vorgabe beim Element E2 eingehalten wird
  Betrachte den Graphen von $f^{'} (x)$ und lasse Dir im Intervall $[- 4; 4,8]$ den absoluten Hochpunkt anzeigen. Es ist $x_H\approx2{,}3094$ und $y_H\approx0{,}3849$ $\;\Rightarrow\;HP(2{,}31 \mid 0{,}385)$ .
  Ein Tiefpunkt des Graphen von $f^{'} (x)$ liegt bei $x_T\approx-2{,}3094$ und $y_T\approx-0{,}3849$ . Die betragsmäßig größere Steigung befindet sich aber im Randpunkt bei $x = 4,8$ . Hier ist $y\approx-0{,}528\;\Rightarrow\;$ absoluter Tiefpunkt $TP(4{,}8 \mid-0{,}528)$
  Somit liegt die steilste Stelle der Bahn bei $x = 4,8$ vor. Mit $0,528 < 0,85$ wird die Vorgabe eingehalten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte den Graphen von $f^{'} (x)$ und lasse Dir im Intervall $[- 4; 4,8]$ den absoluten Hochpunkt und Tiefpunkt anzeigen.
  Beachte auch die Randwerte in dem Intervall.
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .
Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.
Siehe Abbildung 2:
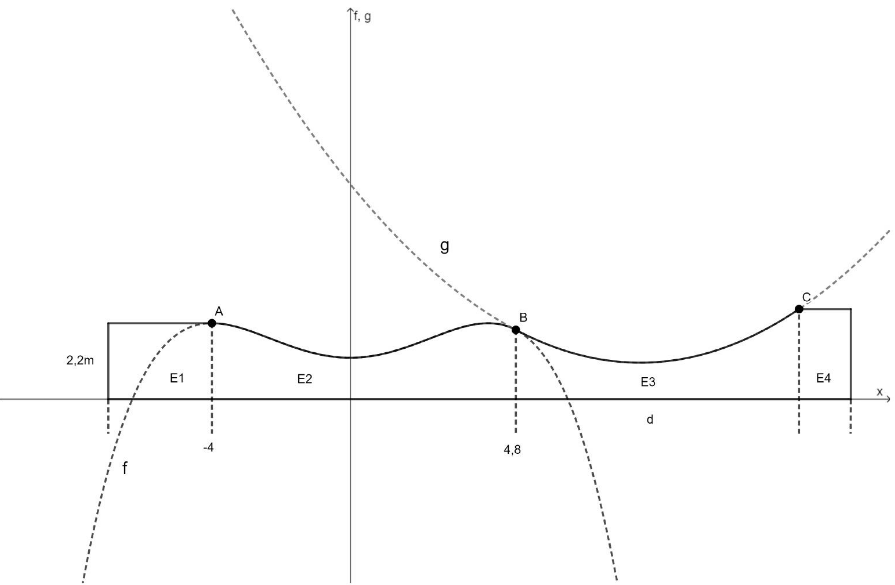
Abbildung 2
Die vier Betonelemente der Skatebahn werden aus einem belastbaren Spezialbeton gegossen. Die Materialkosten hierfür betragen $176\;€$ pro $\mathrm{m}^3$ . Die Skatebahn hat überall eine Breite von $5\mathrm{~m}$ .
1. Ermitteln Sie die Materialkosten für das Element E2. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Ermittele die Materialkosten für das Element E2
  Berechne das Volumen des Elements E2:
  $V=G\cdot h=\left(\displaystyle\int_{-4}^{4{,}8} f(x)\;\mathrm{d} x \right)\cdot 5$ . Man erhält das Volumen in $\mathrm{m}^3$ .
  Die Kosten betragen $176\;€$ pro $\mathrm{m}^3$ , d.h. die Materialkosten für das Element E2 betragen dann $176\cdot V$ :
  Die Kosten sind rund $13239\;€$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne das Volumen des Elements E2 $\;\Rightarrow\;V=\left(\displaystyle\int_{-4}^{4{,}8} f(x)\;\mathrm{d} x \right)\cdot 5$ .
  Die Kosten betragen $176\;€$ pro $\mathrm{m}^3$ , d.h. die Materialkosten für das Element E2 betragen dann $176\cdot V$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .
Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.
Siehe Abbildung 2:
Abbildung 2
Die obere Randlinie von Element E3 soll durch eine ganzrationale Funktion $g$ zweiten Grades modelliert werden, deren Graph im Punkt $B$ sowohl im Funktionswert als auch in der Steigung mit dem Graphen von $f$ übereinstimmt (siehe Abbildung 2). Dabei soll der tiefste Punkt der oberen Randlinie von E3 in $3{,}6\mathrm{~m}$ horizontaler Entfernung vom Punkt $B$ liegen.
1. Ermitteln Sie eine Gleichung der Funktion $g$ . (5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben
  Ermittele eine Gleichung der Funktion $g$
  Gegeben sind $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2$ und die Bedingungen $\mathrm{I}$ und $\mathrm{II}$ .
  $\mathrm{I}\;$ Der Graph von $g$ soll im Punkt $B$ sowohl im Funktionswert als auch in der Steigung mit dem Graphen von $f$ übereinstimmen.
  $\mathrm{II}\;$ Dabei soll der tiefste Punkt der oberen Randlinie von E3 in $3{,}6\mathrm{~m}$ horizontaler Entfernung vom Punkt $B$ liegen.
  Ansatz für eine ganzrationale Funktion $g$ zweiten Grades:
  $g(x)=a \cdot x^{2}+b \cdot x+c$ und $g^{\prime}(x)=2 a \cdot x+b$ .
  Der Punkt $B$ hat die Koordinaten $B (4,8 ∣ 2,0064)$ (aus Aufgabe 1 b) und die Steigung im Punkt $B$ beträgt $f^{'} (4,8) = - 0,528$ (aus Aufgabe 1 d)
  Aus $\mathrm{I}$ folgt dann:
  $g(4{,}8)=f(4{,}8)=2{,}0064\;\Rightarrow\;a\cdot4{,}8^2+b\cdot 4{,}8+c=2{,}0064\\g'(4{,}8)=f'(4{,}8)=-0{,}528\;\Rightarrow\;2a\cdot4{,}8+b=-0{,}528$
  Aus $\mathrm{II}$ folgt:
  Im Tiefpunkt gilt: $g'(4{,}8+3{,}6)=g'(8{,}4)=0\;\Rightarrow\;2a\cdot8{,}4+b=0$
  Zusammengefasst ergibt sich das folgende Gleichungssystem:
  $\def\arraystretch{1.25} \begin{array}{cccccccl}\;\;\;\;\mathrm{(I)}:\;\;\;23{,}04a & + & 4{,}8b& + &c & = & 2{,}0064 \\\mathrm{(II)}:\;\;\; 9{,}6a & + & b & & &=& -0{,}528\\\mathrm{(III)}:\;\; 16{,}8a & + & b & & &=& 0\end{array}$
  Der TR liefert als Lösung:
  $a=\dfrac{11}{150} \approx0{,}073, b=-\dfrac{154}{125}=-1{,}232$ und $c=\dfrac{3894}{625}=6{,}2304$
  Damit folgt für die Gleichung der Funktion $g$ :
  $g(x)=\dfrac{11}{150} x^2-\dfrac{154}{125}x+\dfrac{3894}{625}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben sind $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2$ und die Bedingungen $\mathrm{I}$ und $\mathrm{II}$ .
  $\mathrm{I}\;$ Der Graph von $g$ soll im Punkt $B$ sowohl im Funktionswert als auch in der Steigung mit dem Graphen von $f$ übereinstimmen.
  $\mathrm{II}\;$ Dabei soll der tiefste Punkt der oberen Randlinie von E3 in $3{,}6\mathrm{~m}$ horizontaler Entfernung vom Punkt $B$ liegen.
  Der Ansatz für eine ganzrationale Funktion $g$ zweiten Grades lautet $g(x)=a \cdot x^{2}+b \cdot x+c$ und $g^{\prime}(x)=2 a \cdot x+b$ .
  Erstelle, mit den Bedingungen $\mathrm{I}$ und $\mathrm{II}$ ein lineares Gleichungssystem und löse es mit dem TR.
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .
Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.
Siehe Abbildung 2:
Abbildung 2
Verwenden Sie im Folgenden für die Modellierung von E3 die Gleichung
$g(x)=\frac{11}{150}(x-8{,}4)^{2}+\frac{132}{125}$ .
Ein Übergang ist ruckfrei, wenn an der Übergangsstelle neben den Funktionswerten und den ersten Ableitungen auch die zweiten Ableitungen übereinstimmen.
1. Prüfen Sie, ob es sich beim Übergang von E2 zu E3 um einen ruckfreien Übergang handelt. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Anwendungsaufgaben der Differential- und Integralrechnung
  Prüfe, ob es sich beim Übergang von E2 zu E3 um einen ruckfreien Übergang handelt
  Bekannt ist: Ein Übergang ist ruckfrei, wenn an der Übergangsstelle neben den Funktionswerten und den ersten Ableitungen auch die zweiten Ableitungen übereinstimmen.
  Dabei sind gegeben: $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2$ und $g(x)=\frac{11}{150}(x-8{,}4)^{2}+\frac{132}{125}$
  $\Rightarrow\;f'(x)=-\dfrac{1}{64}x^3+\dfrac{1}{4}x$ und $f''(x)=-\dfrac{3}{64}x^2+\dfrac{1}{4}$ und $g'(x)=\dfrac{11}{75}(x-8{,}4)$ und $g''(x)=\dfrac{11}{75}$
  Ist der Übergang ruckfrei?
  Dann muss gelten:
  $f''(4{,}8)=g''(4{,}8)\;\Rightarrow\;-\dfrac{3}{64}\cdot4{,}8^2+\dfrac{1}{4}\stackrel{?}{=}\dfrac{11}{75}\;\Rightarrow\;-0{,}83\neq0{,}147$
  Die Bedingung ist nicht erfüllt, d.h. der Übergang ist nicht ruckfrei.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Prüfe, ob $f^{''} (4,8) = g^{''} (4,8)$ ist.
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 5
Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .
Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.
Siehe Abbildung 2:
Die vier Betonelemente der Skatebahn werden aus einem belastbaren Spezialbeton gegossen. Die Materialkosten hierfür betragen $176\;€$ pro $\mathrm{m}^3$ . Die Skatebahn hat überall eine Breite von $5\mathrm{~m}$ .
Weiterhin ist $g(x)=\frac{11}{150}(x-8{,}4)^{2}+\frac{132}{125}$ .
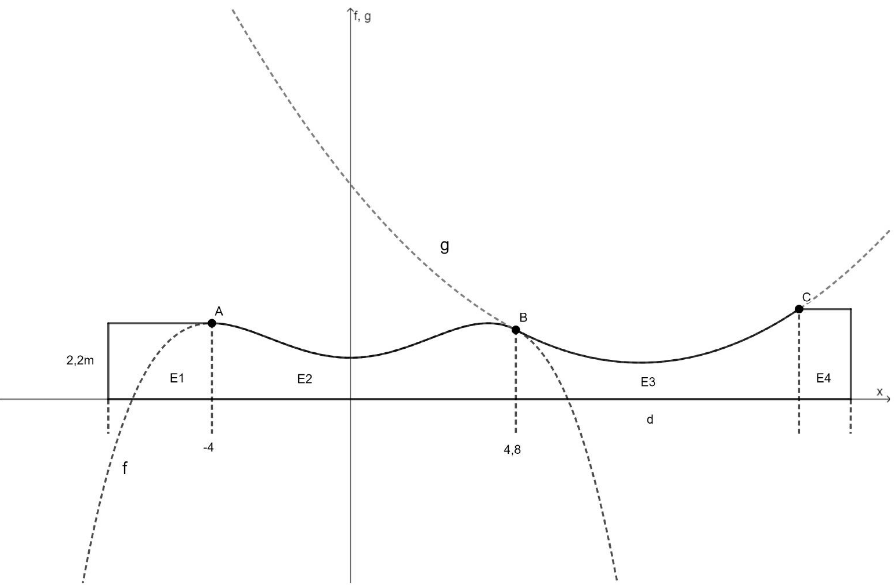
Abbildung 2
Für E3 werden in einem ersten Entwurf zunächst Materialkosten von $10800 €$ veranschlagt.
1. (i) Stellen Sie eine Gleichung auf, mit der die Länge $d$ des Elements E3 so berechnet werden kann, dass die Materialkosten $10800 €$ betragen. (2 P)
  Als Lösung der Gleichung ergibt sich eine Länge von $d \approx 8{,}24\mathrm{~m}$ .
  (ii) Bestimmen Sie die Höhe von E4, die sich damit ergibt. (1 P)
  (iii) Bestimmen Sie die daraus resultierenden Materialkosten für E4 bei einer feststehenden Länge von $1{,}5\mathrm{~m}$ für E4. (1 P)
  $[$ Kontrolllösung: Die Materialkosten für E4 betragen ungefähr $3500 €$ . $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  (i) Stellen Sie eine Gleichung auf, mit der die Länge $d$ des Elements E3 so berechnet werden kann, dass die Materialkosten $10800 €$ betragen
  Das Volumen des Elements E3 in $\mathrm{m}^3$ muss mit den Materialkosten von $176\;€$ pro $\mathrm{m}^3$ multipliziert $10800\;€$ ergeben. Die Grundfläche von E3 ist $G=\displaystyle\int_{4{,}8}^{4{,}8+d} g(x)\; \mathrm{d} x$ und die Höhe beträgt $5\mathrm{~m}$ .
  Es muss also gelten: $176 \cdot 5 \cdot \displaystyle\int_{4{,}8}^{4{,}8+d} g(x)\; \mathrm{d} x=10800$
  (ii) Bestimmen Sie die Höhe von E4, die sich damit ergibt
  Berechne $g(4{,}8+8{,}24)=g(13{,}04)\approx2{,}6348....$ .
  Der Quader E4 ist somit ungefähr $2{,}63\mathrm{~m}$ hoch.
  (iii) Bestimmen Sie die daraus resultierenden Materialkosten für E4 bei einer feststehenden Länge von $1{,}5\mathrm{~m}$ für E4
  Der Quader hat ein Volumen von $V=1{,}5\cdot 2{,}63 \cdot 5=19{,}725\;\mathrm{m}^3$ .
  Die Kosten betragen dann $176 \frac{€}{\mathrm{~m}^{3}} \cdot 19{,}725\;\mathrm{m}^3=3471{,}60\;€$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Die Grundfläche von E3 ist $G=\displaystyle\int_{4{,}8}^{4{,}8+d} g(x)\; \mathrm{d} x$ und die Höhe beträgt $5\mathrm{~m}$ .
  Berechne das Volumen und multipliziere mit $176\;€$ pro $\mathrm{m}^3$ .
  (ii)
  Berechne $g (4,8 + 8,24)$ .
  (iii)
  Berechne das Volumen des Quaders und multipliziere mit $176\;€$ pro $\mathrm{m}^3$ .
2. Dem Architekturbüro wird mitgeteilt, dass für die beiden Elemente E3 und E4 nur Materialkosten von zusammen $12000 €$ entstehen dürfen.
  (i) Berechnen Sie, um wie viel Prozent die Materialkosten beim ersten Entwurf über dieser Vorgabe liegen. (2 P)
  (ii) In einem neuen Entwurf wird daher die Länge von Element E3 verändert.
  Die Länge von Element E4 soll weiterhin $1{,}5\mathrm{~m}$ betragen.
  Stellen Sie eine Gleichung auf, mit der die neue Länge $d_{\text {neu }}$ von Element E3 so berechnet werden kann, dass die Materialkosten von E3 und E4 zusammen genau $12000 €$ betragen. (2 P)
  [Hinweis: Die Gleichung muss nicht gelöst werden.]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Formeln
  (i) Berechne, um wie viel Prozent die Materialkosten beim ersten Entwurf über dieser Vorgabe liegen
  Vorgabe: Die beiden Elemente E3 und E4 dürfen nur Materialkosten von zusammen $12000 €$ verursachen.
  Insgesamt ergeben sich für die Materialkosten von E3 und E4 $10800\;€+3471{,}60\;€=14271{,}60\;€$ .
  Dieser Wert liegt um $\frac{14271{,}60-12000}{12000}=0{,}1893=18{,}93\;\%$ über der Vorgabe.
  (ii) Stelle eine Gleichung auf, mit der die neue Länge $d_{\text {neu }}$ von Element E3 so berechnet werden kann, dass die Materialkosten von E3 und E4 zusammen genau $12000 €$ betragen
  Das neue Volumen von E3 beträgt $V_{E3}=5 \cdot\displaystyle\int_{4{,}8}^{4{,}8+d_{\text {neu }}} g(x) \;\mathrm{d} x$
  Das neue Volumen von E4 beträgt $V_{E4}=1{,}5\cdot 5 \cdot g\left(4{,}8+d_{\text {neu }}\right)$
  Dann soll für die Kosten gelten:
  $176\cdot(V_{E3}+V_{E4})=176\cdot\left(5 \cdot\displaystyle\int_{4{,}8}^{4{,}8+d_{\text {neu }}} g(x) \;\mathrm{d} x+1{,}5\cdot 5 \cdot g\left(4{,}8+d_{\text {neu }}\right)\right)=12000.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Übernimm aus Aufgabe a) die Materialkosten von E3 und E4 und bilde die Summe.
  Berechne die prozentuale Veränderung dieser Summe bezüglich der Vorgabe von $12000 €$ .
  (ii)
  Das neue Volumen von E3 beträgt $V_{E3}=5 \cdot\displaystyle\int_{4{,}8}^{4{,}8+d_{\text {neu }}} g(x) \;\mathrm{d} x$
  Das neue Volumen von E4 beträgt $V_{E4}=1{,}5\cdot 5 \cdot g\left(4{,}8+d_{\text {neu }}\right)$
  Stelle mit der Summe der beiden Volumina eine Gleichung für die Kosten auf, die insgesamt $12000\;€$ betragen sollen.

Aufgabe 6

Die Aufgabe 6 ist eine Fortsetzung der Aufgabe 1.

Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .

Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.

Siehe Abbildung 2:

In einem anderen Skatepark soll der Abschnitt E2 vergleichbar gebaut werden, allerdings soll der Streckenverlauf in diesem Abschnitt steiler sein. Zur Modellierung dient hier eine Funktion $h$ mit

$h(x)=u \cdot\left(-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}\right)+1{,}2, \quad x \in \mathbb{R}, \text { mit } u>0$ .

Begründen Sie, dass $h^{\prime}(x)=u \cdot f^{\prime}(x)$ gilt, und erläutern Sie, wie der Graph von $h^{\prime}$ aus dem Graphen von $f^{\prime}$ hervorgeht. (2 P + 1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Begründe, dass $h^{\prime}(x)=u \cdot f^{\prime}(x)$ gilt
Gegeben ist $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2$ und $h(x)=u \cdot\left(-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}\right)+1{,}2$ .
Dann ist $f'(x)=-\dfrac{1}{64}x^3+\dfrac{1}{4}x$ .
Für $h^{'} (x)$ folgt: $h'(x)=u\cdot\left(-\frac{1}{64} x^{3}+\frac{1}{4} x\right)=u\cdot f'(x)$
Erläutere, wie der Graph von $h^{\prime}$ aus dem Graphen von $f^{\prime}$ hervorgeht
Der Graph von $h^{\prime}$ geht durch eine Streckung in $y$ -Richtung mit einem positiven Streckfaktor $u > 0$ aus dem Graphen von $f^{'}$ hervor.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne die Ableitung von $h (x)$ und vergleiche mit der Ableitung von $f (x)$ .
Teil 2
$f^{'} (x)$ wird mit dem Faktor $u >$ 0 multipliziert. Welche Transformation von $f^{'}$ ist das?

Ermitteln Sie den Wert von $u$ , bei dem diese Bahn im Abschnitt E2 an der Stelle $x = 4,8$ die Steigung $m = - 0,85$ hat. (2 P)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle u\cdot\left(-\frac{1}{64}\cdot 4{,}8^{3}+\frac{1}{4}\cdot 4{,}8\right)$	$=$	$\displaystyle -0{,}85$
	↓	Berechne den Term in der Klammer.
$\displaystyle u\cdot(-0{,}528)$	$=$	$\displaystyle -0{,}85$	$\displaystyle :(-0{,}528)$
$\displaystyle u$	$\approx ≈$	$\displaystyle 1{,}610$

B2

Aufgabe 1

Begründe, dass f(x)=f(−x)f(x)=f(-x)f(x)=f(−x) für alle x∈Rx \in \mathbb{R}x∈R gilt, und interpretieren Sie dies geometrisch

Hast du eine Frage oder Feedback?

Ermittele rechnerisch den Höhenunterschied zwischen dem höchsten und tiefsten Punkt der Skatebahn im Bereich von E2

Hast du eine Frage oder Feedback?

Zeigen Sie, dass die obere Randlinie von Element E2 knickfrei an die obere Randlinie des quaderförmigen Elements E1 anschließt

Hast du eine Frage oder Feedback?

Zeige, dass diese Vorgabe beim Element E2 eingehalten wird

Hast du eine Frage oder Feedback?

Aufgabe 2

Ermittele die Materialkosten für das Element E2

Hast du eine Frage oder Feedback?

Aufgabe 3

Ermittele eine Gleichung der Funktion ggg

Hast du eine Frage oder Feedback?

Aufgabe 4

Prüfe, ob es sich beim Übergang von E2 zu E3 um einen ruckfreien Übergang handelt

Hast du eine Frage oder Feedback?

Aufgabe 5

(i) Stellen Sie eine Gleichung auf, mit der die Länge ddd des Elements E3 so berechnet werden kann, dass die Materialkosten 10800 €10800 ~€10800 € betragen

(ii) Bestimmen Sie die Höhe von E4, die sich damit ergibt

(iii) Bestimmen Sie die daraus resultierenden Materialkosten für E4 bei einer feststehenden Länge von 1,5 m1{,}5\mathrm{~m}1,5 m für E4

Hast du eine Frage oder Feedback?

(i) Berechne, um wie viel Prozent die Materialkosten beim ersten Entwurf über dieser Vorgabe liegen

(ii) Stelle eine Gleichung auf, mit der die neue Länge dneu d_{\text {neu }}dneu ​ von Element E3 so berechnet werden kann, dass die Materialkosten von E3 und E4 zusammen genau 12000 €12000~€12000 € betragen

Hast du eine Frage oder Feedback?

Aufgabe 6

Begründe, dass h′(x)=u⋅f′(x)h^{\prime}(x)=u \cdot f^{\prime}(x)h′(x)=u⋅f′(x) gilt

Erläutere, wie der Graph von h′h^{\prime}h′ aus dem Graphen von f′f^{\prime}f′ hervorgeht

Hast du eine Frage oder Feedback?

Ermittele den Wert von u, bei dem diese Bahn im Abschnitt E2 an der Stelle x=4,8x=4{,}8x=4,8 die Steigung m=−0,85m=-0{,}85m=−0,85 hat

Hast du eine Frage oder Feedback?

Begründe, dass $f (x) = f (- x)$ für alle $x \in \mathbb{R}$ gilt, und interpretieren Sie dies geometrisch

Ermittele eine Gleichung der Funktion $g$

(i) Stellen Sie eine Gleichung auf, mit der die Länge $d$ des Elements E3 so berechnet werden kann, dass die Materialkosten $10800 €$ betragen

(iii) Bestimmen Sie die daraus resultierenden Materialkosten für E4 bei einer feststehenden Länge von $1{,}5\mathrm{~m}$ für E4

(ii) Stelle eine Gleichung auf, mit der die neue Länge $d_{\text {neu }}$ von Element E3 so berechnet werden kann, dass die Materialkosten von E3 und E4 zusammen genau $12000 €$ betragen

Begründe, dass $h^{\prime}(x)=u \cdot f^{\prime}(x)$ gilt

Erläutere, wie der Graph von $h^{\prime}$ aus dem Graphen von $f^{\prime}$ hervorgeht

Ermittele den Wert von u, bei dem diese Bahn im Abschnitt E2 an der Stelle $x = 4,8$ die Steigung $m = - 0,85$ hat