Aufgabe 1
In einem Skatepark soll ein neuer Teilabschnitt gebaut werden. Der Entwurf des Architekten für den Längsschnitt des Abschnitts ist in Abbildung 1 zu sehen.
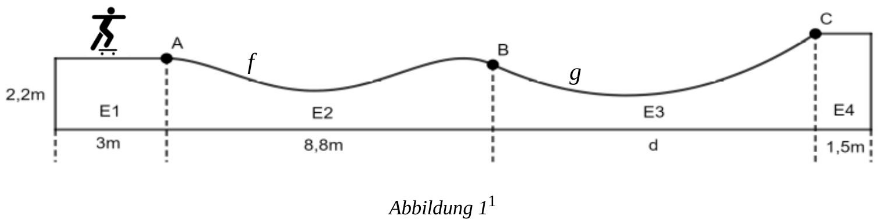
Der Abschnitt soll aus vier Betonelementen mit senkrechten Seitenwänden zusammengesetzt werden. Die äußeren Elemente E1 und E4 sind quaderförmig, für die beiden mittleren Elemente E2 und E3 werden die in Abbildung 1 dargestellten oberen Randlinien durch zwei ganzrationale Funktionen und modelliert (Abbildung 2). Die in Abbildung 1 dargestellten unteren Randlinien aller vier Elemente werden durch die -Achse modelliert.
Außer beim Übergang von E3 zu E4 sollen die dargestellten oberen Randlinien der Elemente „knickfrei“ ineinander übergehen, um ein störungsfreies Fahren zu gewährleisten.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für die Funktion mit .
Dabei entspricht eine Längeneinheit im Koordinatensystem in der Realität.
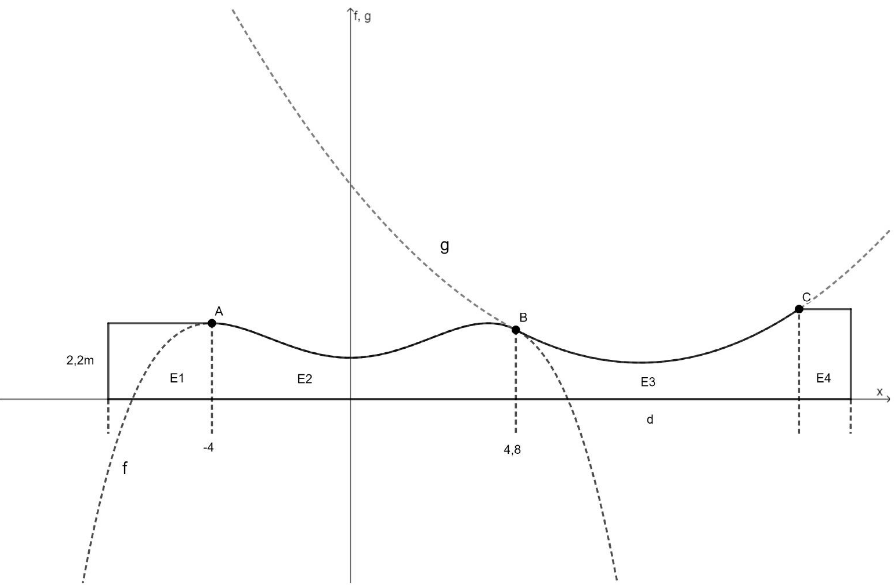
Abbildung 2
Begründen Sie, dass für alle gilt, und interpretieren Sie dies geometrisch. (1 P + 1 P)
Ermitteln Sie rechnerisch den Höhenunterschied zwischen dem höchsten und tiefsten Punkt der Skatebahn im Bereich von E2. (4 P)
Zeigen Sie, dass die obere Randlinie von Element E2 knickfrei an die obere Randlinie des quaderförmigen Elements E1 anschließt. (2 P)
Aus Sicherheitsgründen soll an der steilsten Stelle der Bahn der Betrag der Steigung höchstens sein.
Zeigen Sie, dass diese Vorgabe beim Element E2 eingehalten wird. (4 P)

