Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für die Funktion mit .
Dabei entspricht eine Längeneinheit im Koordinatensystem in der Realität.
Siehe Abbildung 2:
Die vier Betonelemente der Skatebahn werden aus einem belastbaren Spezialbeton gegossen. Die Materialkosten hierfür betragen pro . Die Skatebahn hat überall eine Breite von .
Verwenden Sie im Folgenden für die Modellierung von E3 die Gleichung .
Für E3 werden in einem ersten Entwurf zunächst Materialkosten von veranschlagt.
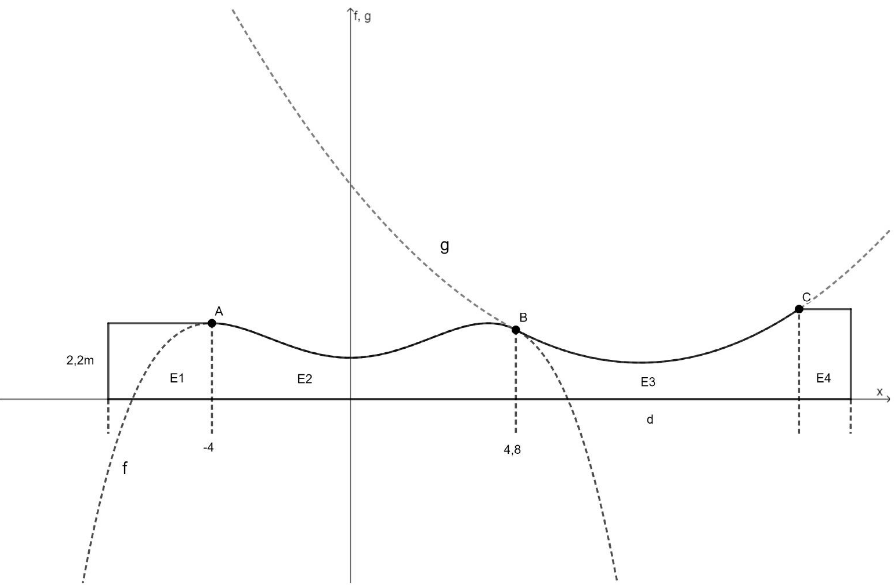
Abbildung 2
(i) Stellen Sie eine Gleichung auf, mit der die Länge des Elements E3 so berechnet werden kann, dass die Materialkosten betragen. (2 P)
Als Lösung der Gleichung ergibt sich eine Länge von .
(ii) Bestimmen Sie die daraus resultierenden Materialkosten für E4 bei einer feststehenden Länge von für E4. (2 P)
Kontrolllösung: Die Materialkosten für E4 betragen ungefähr .
Dem Architekturbüro wird mitgeteilt, dass für die beiden Elemente E3 und E4 nur Materialkosten von zusammen entstehen dürfen.
(i) Berechnen Sie, um wie viel Prozent die Materialkosten beim ersten Entwurf über dieser Vorgabe liegen. (2 P)
(ii) In einem neuen Entwurf wird daher die Länge von Element E3 verändert.
Die Länge von Element E4 soll weiterhin betragen.
Stellen Sie eine Gleichung auf, mit der die neue Länge von Element E3 so berechnet werden kann, dass die Materialkosten von E3 und E4 zusammen genau betragen. (2 P)
[Hinweis: Die Gleichung muss nicht gelöst werden.]
