B4 - lernen mit Serlo!

Aufgabe 5

Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.

„Schraubenwind“ stellt noch einen zweiten Schraubentyp her. Die Schichtdicke (gemessen in $μ m$ ⁣) einer zufällig ausgewählten Schraube dieses Typs lässt sich näherungsweise durch eine Normalverteilung mit $μ = 8,2$ und $σ = 0,4$ (beides in $μ m$ ⁣) beschreiben.

Ermitteln Sie die Wahrscheinlichkeit, dass die Schichtdicke (in $μ m$ ⁣) einer zufällig ausgewählten Schraube zwischen $7,5$ und $8,5$ liegt. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Ermittele die Wahrscheinlichkeit, dass die Schichtdicke (in $μ m$ ⁣) einer zufällig ausgewählten Schraube zwischen $7,5$ und $8,5$ liegt
Gegeben ist eine Normalverteilung mit $μ = 8,2$ und $σ = 0,4$ .
Der TR liefert $P (7,5 \leq X \leq 8,5) \approx 0,7333$ .
Die Wahrscheinlichkeit, dass die Schichtdicke einer Schraube in dem geforderten Intervall liegt, beträgt daher ca. $73,33 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne für eine Normalverteilung $P (7,5 \leq X \leq 8,5)$ .
Zu einer Normalverteilung mit der Dichtefunktion $φ$ bezeichnet man die Funktion $Φ$ mit $Φ (x) = \int_{- \infty}^{x} φ (t) d t$ als Verteilungsfunktion.
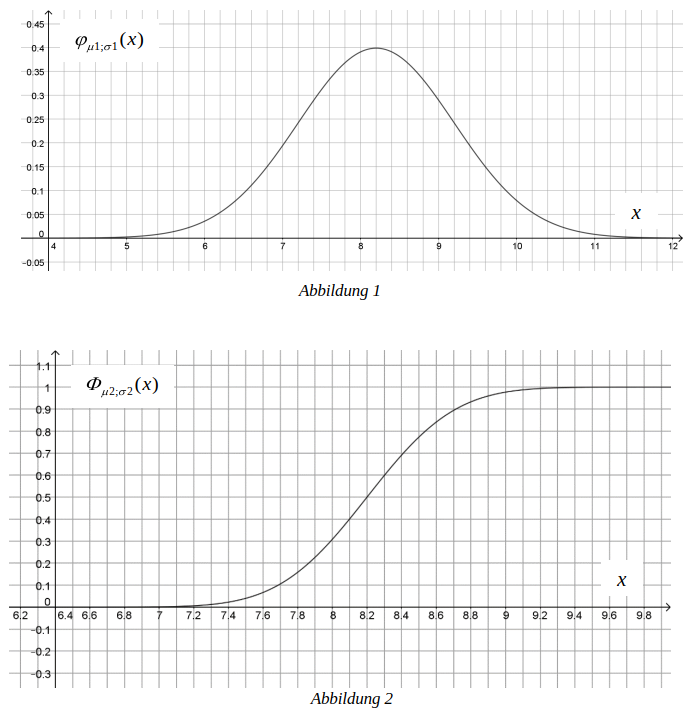
In Abbildung 1 ist die Dichtefunktion einer Normalverteilung dargestellt.
Entscheiden Sie für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern $μ = 8,2$ und $σ = 0,4$ handeln kann.
(2 P + 2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Entscheide für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern $μ = 8,2$ und $σ = 0,4$ handeln kann
Abbildung 1:
Der Erwartungswert passt:
Die Maximalstelle des Graphen ist $x = 8,2$ .
Bei einer Standardabweichung von $0,4$ gilt: $P (8,2 - 3 \cdot 0,4 \leq X \leq 8,2 + 3 \cdot 0,4) = P (7 \leq X \leq 9,4) \approx 1$ .
Es ist aber deutlich erkennbar, dass außerhalb des Intervalls $[7; 9,4]$ erhebliche Flächenteile übrig bleiben.
Der Graph passt also nicht zu den gegebenen Parametern.
Abbildung 2:
Der Erwartungswert passt:
$y = 0,5$ wird an der Stelle $x = 8,2$ angenommen.
Bei einer Standardabweichung von $0,4$ werden Werte innerhalb des Intervalls
$[8,2 - 0,4; 8,2 + 0,4] = [7,8; 8,6]$ mit einer Wahrscheinlichkeit von ca. $68 %$ angenommen. Werte im Intervall $[- \infty; 7,8]$ haben damit eine Wahrscheinlichkeit von ca. $\frac{1 - 0,68}{2} = 0,16 = 16 %$ . An der Stelle $x = 7,8$ beträgt der y-Wert ca. $0,16$ .
Der Graph passt daher zu den gegebenen Parametern.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Abbildung 1:
Prüfe, ob die Maximalstelle des Graphens bei x=8,2 liegt.
Bei einer Standardabweichung von $0,4$ gilt: $P (7 \leq X \leq 9,4) \approx 1$ .
In der Abbildung bleiben außerhalb des Intervalls $[7; 9,4]$ erhebliche Flächenteile übrig. Was bedeutet das?
Abbildung 2:
An der Stelle $x = 8,2$ muss $y = 0,5$ sein. Stimmt das?
Innerhalb einer 1- $σ$ -Umgebung von $μ$ liegen die Werte innerhalb des Intervalls $[7,8; 8,6]$ mit einer Wahrscheinlichkeit von ca. $68 %$ . Werte im Intervall $[- \infty; 7,8]$ haben eine Wahrscheinlichkeit von ca. $16 %$ .
Wie groß ist an der Stelle $x = 7,8$ der y-Wert? Entspricht dieser Wert $16 %$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 5

Ermittele die Wahrscheinlichkeit, dass die Schichtdicke (in μm⁣) einer zufällig ausgewählten Schraube zwischen 7,5 und 8,5 liegt

Hast du eine Frage oder Feedback?

Entscheide für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern μ=8,2 und σ=0,4 handeln kann

Hast du eine Frage oder Feedback?

Ermittele die Wahrscheinlichkeit, dass die Schichtdicke (in $μ m$ ⁣) einer zufällig ausgewählten Schraube zwischen $7,5$ und $8,5$ liegt

Entscheide für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern $μ = 8,2$ und $σ = 0,4$ handeln kann