B4

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Die Firma „Schraubenwind“ stellt Schrauben und Muttern für den Bau von Windkraftanlagen her. Wegen der extremen Belastung werden besondere Anforderungen an diese Verbindungselemente gestellt. Eine hochwertige Schraube zeichnet sich durch die Qualität des Schraubenkörpers und die Qualität der anschließenden Beschichtung aus.
1. Bei der Produktion entstehen immer wieder Schrauben, die nicht den Qualitätsansprüchen von „Schraubenwind“ genügen. $97 %$ der Schrauben weisen einen fehlerfreien Schraubenkörper auf. Von den Schrauben mit fehlerfreiem Schraubenkörper haben $1,5 %$ eine fehlerhafte Beschichtung. Von den Schrauben mit fehlerhaftem Schraubenkörper haben $5 %$ eine fehlerhafte Beschichtung.
  Stellen Sie den beschriebenen Sachzusammenhang im folgenden Baumdiagramm dar. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Stelle den beschriebenen Sachzusammenhang im folgenden Baumdiagramm dar
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Übertrage die gegebenen Werte in ein Baumdiagramm.
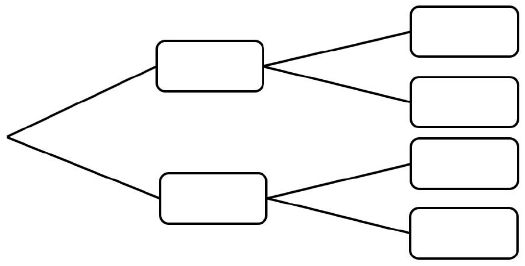
2. Die Beschichtung einer zufällig ausgewählten Schraube ist fehlerhaft.
  Bestimmen Sie die Wahrscheinlichkeit, dass diese Schraube einen fehlerhaften Schraubenkörper aufweist. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
  Bestimme die Wahrscheinlichkeit, dass diese Schraube einen fehlerhaften Schraubenkörper aufweist
  Falls eine (zufällig gewählte) Schraube eine fehlerhafte Beschichtung aufweist, beträgt die Wahrscheinlichkeit, dass der Schraubenkörper fehlerhaft ist
  Berechne die bedingte Wahrscheinlichkeit
  $P_{B -} (K -) = \frac{P (K - \cap B -)}{P (B -)} = \frac{0,03 \cdot 0,05}{0,03 \cdot 0,05 + 0,97 \cdot 0,015} \approx 0,09346$ .
  Die Wahrscheinlichkeit, dass diese Schraube einen fehlerhaften Schraubenkörper aufweist, beträgt etwa $9,346 % .$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die bedingte Wahrscheinlichkeit $P_{B -} (K -) = \frac{P (K - \cap B -)}{P (B -)}$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Im Folgenden gilt eine Schraube als fehlerfrei, wenn sowohl der Schraubenkörper als auch
die Beschichtung fehlerfrei sind. Qualitätskontrollen bei der Firma „Schraubenwind“ zeigen, dass im Durchschnitt $4,5 %$ der Schrauben fehlerhaft die Produktion verlassen. Im Folgenden wird modellhaft davon ausgegangen, dass die Anzahl an fehlerhaften Schrauben in der Produktion binomialverteilt mit $p = 0,045$ ist.
1. In einer Untersuchung werden $500$ Schrauben zufällig der Produktion entnommen. Bestimmen Sie die Wahrscheinlichkeit, dass unter diesen Schrauben genau $15$ Schrauben fehlerhaft sind. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Bestimme die Wahrscheinlichkeit, dass unter diesen Schrauben genau $15$ Schrauben fehlerhaft sind
  Die Anzahl an fehlerhaften Schrauben in der Produktion ist binomialverteilt mit $p = 0,045$ und $n = 500$ .
  Berechne $P (X = 15) = binomPdf (500, 0.045, 15) \approx 0,0238$
  Die Wahrscheinlichkeit, dass unter diesen Schrauben genau $15$ Schrauben fehlerhaft sind, beträgt rund $2,38 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $P (X = 15)$ .
2. Ermitteln Sie, wie viele Schrauben mindestens entnommen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens $95 %$ mindestens $200$ dieser Schrauben fehlerfrei sind. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreimal-Mindestens-Aufgaben
  Ermittele, wie viele Schrauben mindestens entnommen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens $95 %$ mindestens $200$ dieser Schrauben fehlerfrei sind
  Mit $p = 1 - 0,045 = 0,955$ gilt:
  Gesucht wird der kleinste Wert für $n$ mit $P_{n; 0,955} (X \geq 200) \geq 0,95$ .
  Der TR liefert $P_{214; 0,955} (X \geq 200) = binomCdf (214, 0.955, 200,214) \approx 0,9388$ und $P_{215; 0,955} (X \geq 200) = binomCdf (215, 0.955, 200,215) \approx 0,9652$ .
  Es müssen also mindestens $215$ Schrauben kontrolliert werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gesucht wird der kleinste Wert für $n$ mit $P_{n; 0,955} (X \geq 200) \geq 0,95$ .
  Probiere mehrere Werte für $n$ aus.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
„Wind 24“, ein Hersteller von Windkraftanlagen, benötigt $5000$ fehlerfreie Schrauben.
„Wind 24“ gibt bei der Firma „Schraubenwind“ eine Bestellung auf.
1. Ermitteln Sie, wie viele Schrauben mindestens produziert werden müssen, damit der Erwartungswert für fehlerfreie Schrauben in dieser Produktion mindestens $5000$ beträgt. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
  Ermittele, wie viele Schrauben mindestens produziert werden müssen, damit der Erwartungswert für fehlerfreie Schrauben in dieser Produktion mindestens $5000$ beträgt
  Für "fehlerfrei" ist $p = 0,955 \Rightarrow μ = 5000 = n \cdot 0,955 \Rightarrow n = \frac{5000}{0,955} \approx 5235,6$
  Es müssen also mindestens $5236$ Schrauben produziert werden, damit der Erwartungswert für fehlerfreie Schrauben mindestens $5000$ beträgt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für "fehlerfrei" ist $p = 0,955 \Rightarrow μ = 5000 = n \cdot 0,955$ .
  Löse nach $n$ auf.
2. Es werden $5236$ Schrauben produziert.
  Ermitteln Sie die Wahrscheinlichkeit, dass die Anzahl an fehlerfreien Schrauben in dieser Produktion für den Bedarf von „Wind 24“ ausreicht. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Ermittele die Wahrscheinlichkeit, dass die Anzahl an fehlerfreien Schrauben in dieser Produktion für den Bedarf von „Wind 24“ ausreicht
  Berechne $P_{5236; 0,955} (X \geq 5000) = binomCdf (5236, 0.955, 5000,5236) \approx 0,5274$ .
  Wenn $5236$ Schrauben produziert werden, beträgt die Wahrscheinlichkeit, dass die Anzahl an fehlerfreien Schrauben in dieser Produktion für den Bedarf von „Wind 24“ ausreicht, rund $52,74 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $P_{5236; 0,955} (X \geq 5000)$ .
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
„Wind 24“ beschwert sich bei „Schraubenwind“. Die Qualität der gelieferten Schrauben habe stark nachgelassen: Ca. $8 %$ der gelieferten Schrauben seien fehlerhaft. „Schraubenwind“ entscheidet sich, dem Vorwurf nachzugehen. Es werden $200$ Schrauben zufällig der laufenden Produktion entnommen und auf ihre Qualität hin untersucht. „Wind 24“ ist der wichtigste Kunde von „Schraubenwind“. Die Firmenleitung will daher die Wahrscheinlichkeit, dass sie die Beschwerde von „Wind 24“ zurückweist, obwohl die Schrauben tatsächlich eine Fehlerquote von $8 %$ aufweisen, begrenzen. Sie führt dazu einen Hypothesentest auf einem Signifikanzniveau von $5 %$ durch.
1. Bestimmen Sie eine Entscheidungsregel für den obigen Hypothesentest. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Bestimme eine Entscheidungsregel für den obigen Hypothesentest
  Es ist $p = 0,08$ und $n = 200$ .
  Hypothesentest auf einem Signifikanzniveau von $5 %$ .
  Da kleine Anzahlen an fehlerhaften Schrauben gegen eine erhöhte Fehlerquote sprechen, testet man linksseitig.
  Der TR liefert $P_{200; 0,08} (X \leq 9) = binomCdf (200, 0.08, 0,9) \approx 0,03737$ und
  $P_{200; 0,08} (X \leq 10) = binomCdf (200, 0.08, 0,10) \approx 0,06913$ .
  Die Entscheidungsregel lautet daher:
  „Weise den Vorwurf von „Wind 24“ zurück, wenn $9$ oder weniger fehlerhafte Schrauben unter den $200$ untersuchten Schrauben sind.“
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Hypothesentest auf einem Signifikanzniveau von $5 %$ .
  Es ist $p = 0,08$ und $n = 200$ .
  Berechne $P_{200; 0,08} (X \leq 9)$ und $P_{200; 0,08} (X \leq 10)$ .
  Welcher Wert liegt unter $5 %$ ?
2. Ermitteln Sie die Wahrscheinlichkeit, dass die Firmenleitung die Beschwerde von „Wind 24“ nicht zurückweist, falls der Produktionsprozess nach wie vor nur eine Fehlerquote von $4,5 %$ aufweist. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Ermittele die Wahrscheinlichkeit, dass die Firmenleitung die Beschwerde von „Wind 24“ nicht zurückweist, falls der Produktionsprozess nach wie vor nur eine Fehlerquote von $4,5 %$ aufweist
  Der TR liefert $P_{200; 0,045} (X \geq 10) = binomCdf (200, 0.045, 10,200) \approx 0,4126$ .
  Falls die Fehlerquote nach wie vor nur $4,5 %$ beträgt, liegt die Wahrscheinlichkeit, dass „Schraubenwind“ die Beschwerde von „Wind 24“ nicht zurückweist, bei ca. $41,26 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $P_{200; 0,045} (X \geq 10)$ .
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 5
Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.
„Schraubenwind“ stellt noch einen zweiten Schraubentyp her. Die Schichtdicke (gemessen in $μ m$ ⁣) einer zufällig ausgewählten Schraube dieses Typs lässt sich näherungsweise durch eine Normalverteilung mit $μ = 8,2$ und $σ = 0,4$ (beides in $μ m$ ⁣) beschreiben.
1. Ermitteln Sie die Wahrscheinlichkeit, dass die Schichtdicke (in $μ m$ ⁣) einer zufällig ausgewählten Schraube zwischen $7,5$ und $8,5$ liegt. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Ermittele die Wahrscheinlichkeit, dass die Schichtdicke (in $μ m$ ⁣) einer zufällig ausgewählten Schraube zwischen $7,5$ und $8,5$ liegt
  Gegeben ist eine Normalverteilung mit $μ = 8,2$ und $σ = 0,4$ .
  Der TR liefert $P (7,5 \leq X \leq 8,5) \approx 0,7333$ .
  Die Wahrscheinlichkeit, dass die Schichtdicke einer Schraube in dem geforderten Intervall liegt, beträgt daher ca. $73,33 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne für eine Normalverteilung $P (7,5 \leq X \leq 8,5)$ .
2. Zu einer Normalverteilung mit der Dichtefunktion $φ$ bezeichnet man die Funktion $Φ$ mit $Φ (x) = \int_{- \infty}^{x} φ (t) d t$ als Verteilungsfunktion.
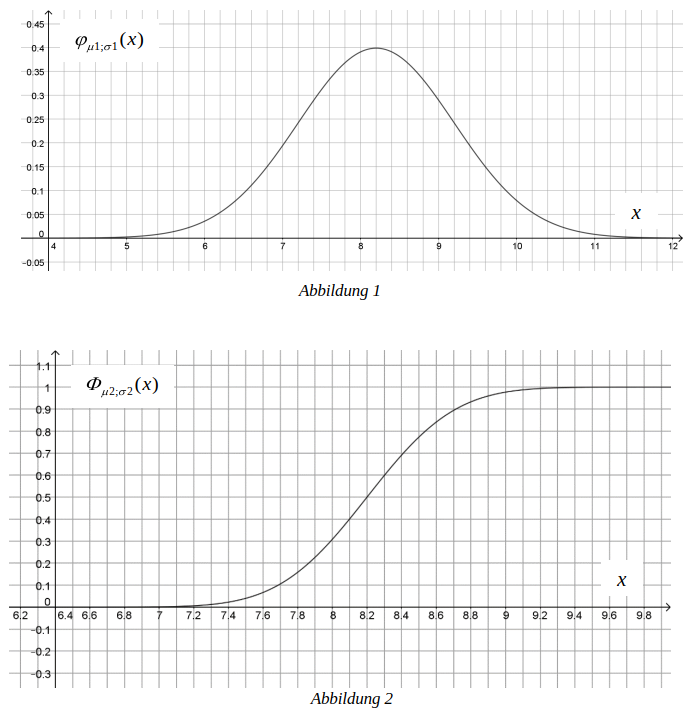
  In Abbildung 1 ist die Dichtefunktion einer Normalverteilung dargestellt.
  Entscheiden Sie für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern $μ = 8,2$ und $σ = 0,4$ handeln kann.
  (2 P + 2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Entscheide für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern $μ = 8,2$ und $σ = 0,4$ handeln kann
  Abbildung 1:
  Der Erwartungswert passt:
  Die Maximalstelle des Graphen ist $x = 8,2$ .
  Bei einer Standardabweichung von $0,4$ gilt: $P (8,2 - 3 \cdot 0,4 \leq X \leq 8,2 + 3 \cdot 0,4) = P (7 \leq X \leq 9,4) \approx 1$ .
  Es ist aber deutlich erkennbar, dass außerhalb des Intervalls $[7; 9,4]$ erhebliche Flächenteile übrig bleiben.
  Der Graph passt also nicht zu den gegebenen Parametern.
  Abbildung 2:
  Der Erwartungswert passt:
  $y = 0,5$ wird an der Stelle $x = 8,2$ angenommen.
  Bei einer Standardabweichung von $0,4$ werden Werte innerhalb des Intervalls
  $[8,2 - 0,4; 8,2 + 0,4] = [7,8; 8,6]$ mit einer Wahrscheinlichkeit von ca. $68 %$ angenommen. Werte im Intervall $[- \infty; 7,8]$ haben damit eine Wahrscheinlichkeit von ca. $\frac{1 - 0,68}{2} = 0,16 = 16 %$ . An der Stelle $x = 7,8$ beträgt der y-Wert ca. $0,16$ .
  Der Graph passt daher zu den gegebenen Parametern.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Abbildung 1:
  Prüfe, ob die Maximalstelle des Graphens bei x=8,2 liegt.
  Bei einer Standardabweichung von $0,4$ gilt: $P (7 \leq X \leq 9,4) \approx 1$ .
  In der Abbildung bleiben außerhalb des Intervalls $[7; 9,4]$ erhebliche Flächenteile übrig. Was bedeutet das?
  Abbildung 2:
  An der Stelle $x = 8,2$ muss $y = 0,5$ sein. Stimmt das?
  Innerhalb einer 1- $σ$ -Umgebung von $μ$ liegen die Werte innerhalb des Intervalls $[7,8; 8,6]$ mit einer Wahrscheinlichkeit von ca. $68 %$ . Werte im Intervall $[- \infty; 7,8]$ haben eine Wahrscheinlichkeit von ca. $16 %$ .
  Wie groß ist an der Stelle $x = 7,8$ der y-Wert? Entspricht dieser Wert $16 %$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B4

Aufgabe 1

Stelle den beschriebenen Sachzusammenhang im folgenden Baumdiagramm dar

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit, dass diese Schraube einen fehlerhaften Schraubenkörper aufweist

Hast du eine Frage oder Feedback?

Aufgabe 2

Bestimme die Wahrscheinlichkeit, dass unter diesen Schrauben genau 15 Schrauben fehlerhaft sind

Hast du eine Frage oder Feedback?

Ermittele, wie viele Schrauben mindestens entnommen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens 95% mindestens 200 dieser Schrauben fehlerfrei sind

Hast du eine Frage oder Feedback?

Aufgabe 3

Ermittele, wie viele Schrauben mindestens produziert werden müssen, damit der Erwartungswert für fehlerfreie Schrauben in dieser Produktion mindestens 5000 beträgt

Hast du eine Frage oder Feedback?

Ermittele die Wahrscheinlichkeit, dass die Anzahl an fehlerfreien Schrauben in dieser Produktion für den Bedarf von „Wind 24“ ausreicht

Hast du eine Frage oder Feedback?

Aufgabe 4

Bestimme eine Entscheidungsregel für den obigen Hypothesentest

Hast du eine Frage oder Feedback?

Ermittele die Wahrscheinlichkeit, dass die Firmenleitung die Beschwerde von „Wind 24“ nicht zurückweist, falls der Produktionsprozess nach wie vor nur eine Fehlerquote von 4,5% aufweist

Hast du eine Frage oder Feedback?

Aufgabe 5

Ermittele die Wahrscheinlichkeit, dass die Schichtdicke (in μm⁣) einer zufällig ausgewählten Schraube zwischen 7,5 und 8,5 liegt

Hast du eine Frage oder Feedback?

Entscheide für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern μ=8,2 und σ=0,4 handeln kann

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit, dass unter diesen Schrauben genau $15$ Schrauben fehlerhaft sind

Ermittele, wie viele Schrauben mindestens entnommen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens $95 %$ mindestens $200$ dieser Schrauben fehlerfrei sind

Ermittele, wie viele Schrauben mindestens produziert werden müssen, damit der Erwartungswert für fehlerfreie Schrauben in dieser Produktion mindestens $5000$ beträgt

Ermittele die Wahrscheinlichkeit, dass die Firmenleitung die Beschwerde von „Wind 24“ nicht zurückweist, falls der Produktionsprozess nach wie vor nur eine Fehlerquote von $4,5 %$ aufweist

Ermittele die Wahrscheinlichkeit, dass die Schichtdicke (in $μ m$ ⁣) einer zufällig ausgewählten Schraube zwischen $7,5$ und $8,5$ liegt

Entscheide für beide Abbildungen jeweils begründet, ob es sich um eine Normalverteilung mit den Parametern $μ = 8,2$ und $σ = 0,4$ handeln kann