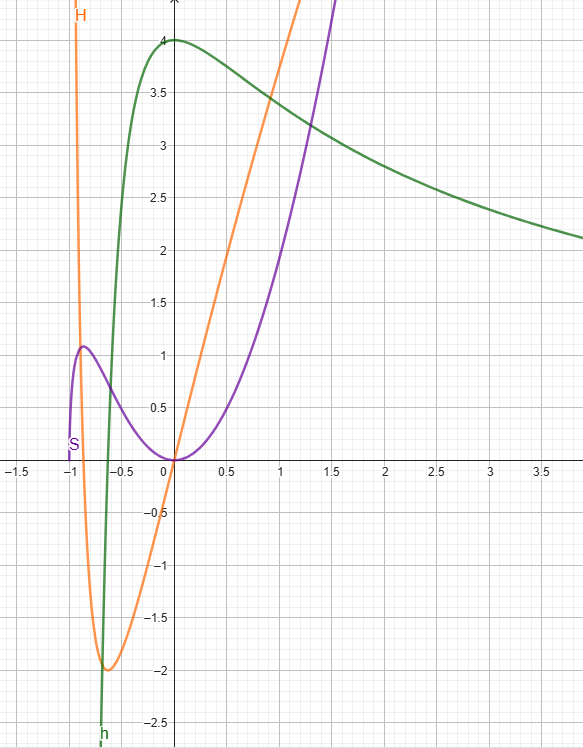
Gegeben ist die Funktion mit der Definitionsmenge .
Berechnen Sie die Nullstelle von . Bestimmen Sie außerdem das Verhalten der Funktionswerte für .
Ermitteln Sie die Wertemenge von .
Gegeben ist nun die Funktion mit der Definitionsmenge .
Bestimmen Sie eine integralfreie Darstellung von .
Hinweis: Die Substitution kann hilfreich sein.
Die Funktion sei eine Stammfunktion von mit der Definitionsmenge .
Begründen Sie, dass der Graph von einen Extrempunkt bei besitzt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?