Aufgabenteil a.)

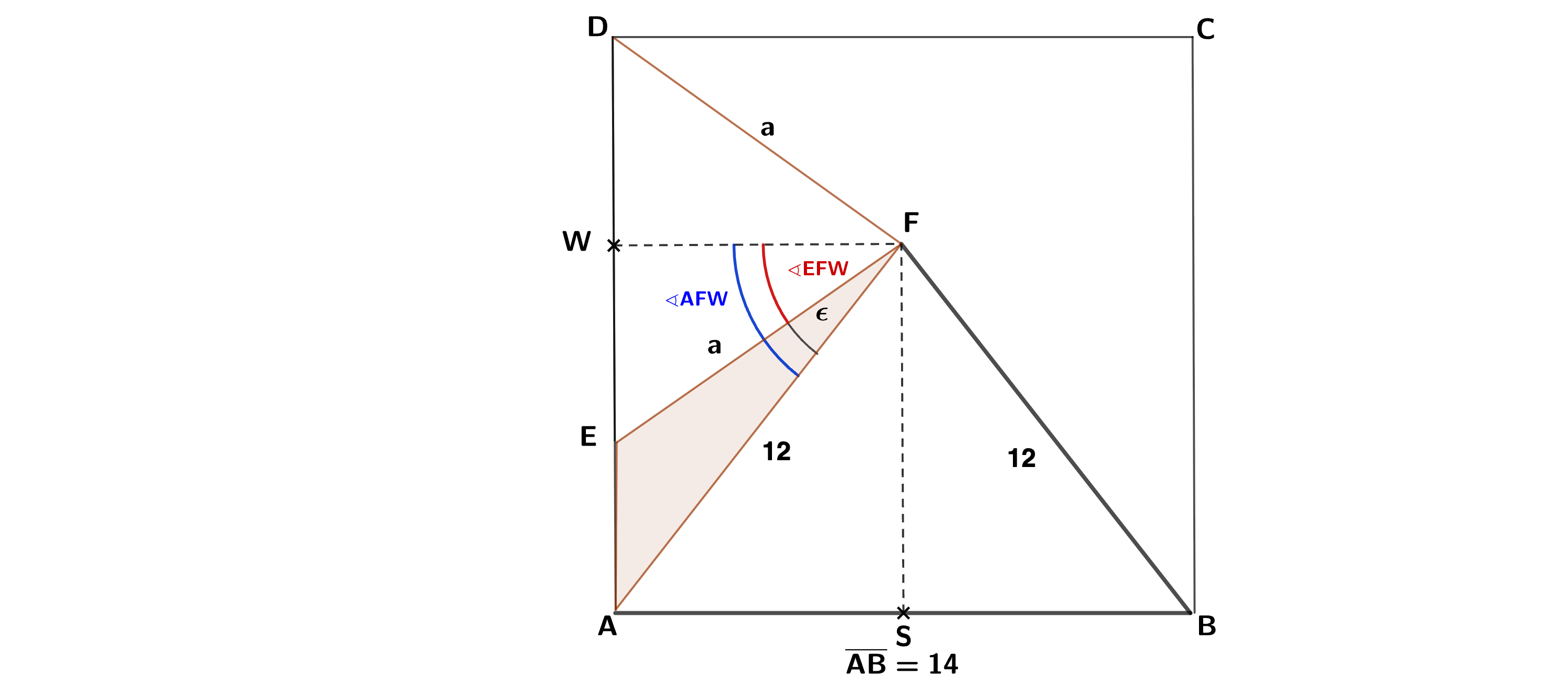
Berechnen des Flächeninhalts des Dreiecks $\text{𝐀𝐅𝐄}$

Berechnen der Strecke: $\overline{\mathrm{A}\mathrm{S}}$

$\overline{\mathrm{A}\mathrm{S}}={\displaystyle \frac{\overline{\mathrm{A}\mathrm{B}}}{2}}$ da das Dreieck $\mathrm{ABF}$ gleichschenklig ist.

$\overline{\mathrm{A}\mathrm{S}}={\displaystyle \frac{14}{2}}\Rightarrow \overline{\mathrm{A}\mathrm{S}}=7\text{ cm}$

Berechnen der Strecke: $\overline{\mathrm{A}\mathrm{E}}$

$\overline{\mathrm{A}\mathrm{E}}=\overline{\mathrm{A}\mathrm{D}}-\overline{\mathrm{D}\mathrm{E}}$

Berechnen der Strecke: $\overline{\mathrm{D}\mathrm{E}}$

$\overline{\mathrm{D}\mathrm{E}}=2\cdot \overline{\mathrm{D}\mathrm{W}}$da das Dreieck $\mathrm{EFD}$ gleichschenklig ist.

$\overline{\mathrm{D}\mathrm{W}}=\overline{\mathrm{A}\mathrm{D}}-\overline{\mathrm{F}\mathrm{S}}\overline{\mathrm{F}\mathrm{S}}=\sqrt{{12}^2-7^2}\Rightarrow \overline{\mathrm{F}\mathrm{S}}=\sqrt{95}$

$\overline{\mathrm{F}\mathrm{S}}=\mathrm{9,75}\mathrm{c}\mathrm{m}$

$\overline{\mathrm{D}\mathrm{W}}=14-\mathrm{9,75}\Rightarrow \overline{\mathrm{D}\mathrm{W}}=\mathrm{4,25}\text{ cm}$

$\overline{\mathrm{D}\mathrm{E}}=2\cdot \mathrm{4,25}\Rightarrow \overline{\mathrm{D}\mathrm{E}}=\mathrm{8,50}\text{ cm}$

$\overline{\mathrm{A}\mathrm{E}}=14-\mathrm{8,50}\Rightarrow \overline{\mathrm{A}\mathrm{E}}=\mathrm{5,50}\text{ cm}$

Die Formel zur Berechnung des Flächeninhalts eines Dreiecks lautet:

${\mathrm{A}}_{\mathrm{D}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{e}\mathrm{c}\mathrm{k}}={\displaystyle \frac{\mathrm{g}\cdot \mathrm{h}}{2}}$

für das Dreieck $\text{AFE}$ gilt:

${\mathrm{A}}_{\mathrm{D}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{e}\mathrm{c}\mathrm{k}}={\displaystyle \frac{\overline{\mathrm{A}\mathrm{E}}\cdot \overline{\mathrm{A}\mathrm{S}}}{2}}\Rightarrow {\mathrm{A}}_{\mathrm{D}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{e}\mathrm{c}\mathrm{k}}={\displaystyle \frac{\mathrm{5,50}\cdot 7}{2}}$

${\mathrm{A}}_{\mathrm{D}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{e}\mathrm{c}\mathrm{k}}=\mathrm{19,25}{\text{ cm}}^2$

Der Flächeninhalt des Dreiecks $\text{AFE}$ beträgt, $\mathrm{19,25}{\text{ cm}}^2$.

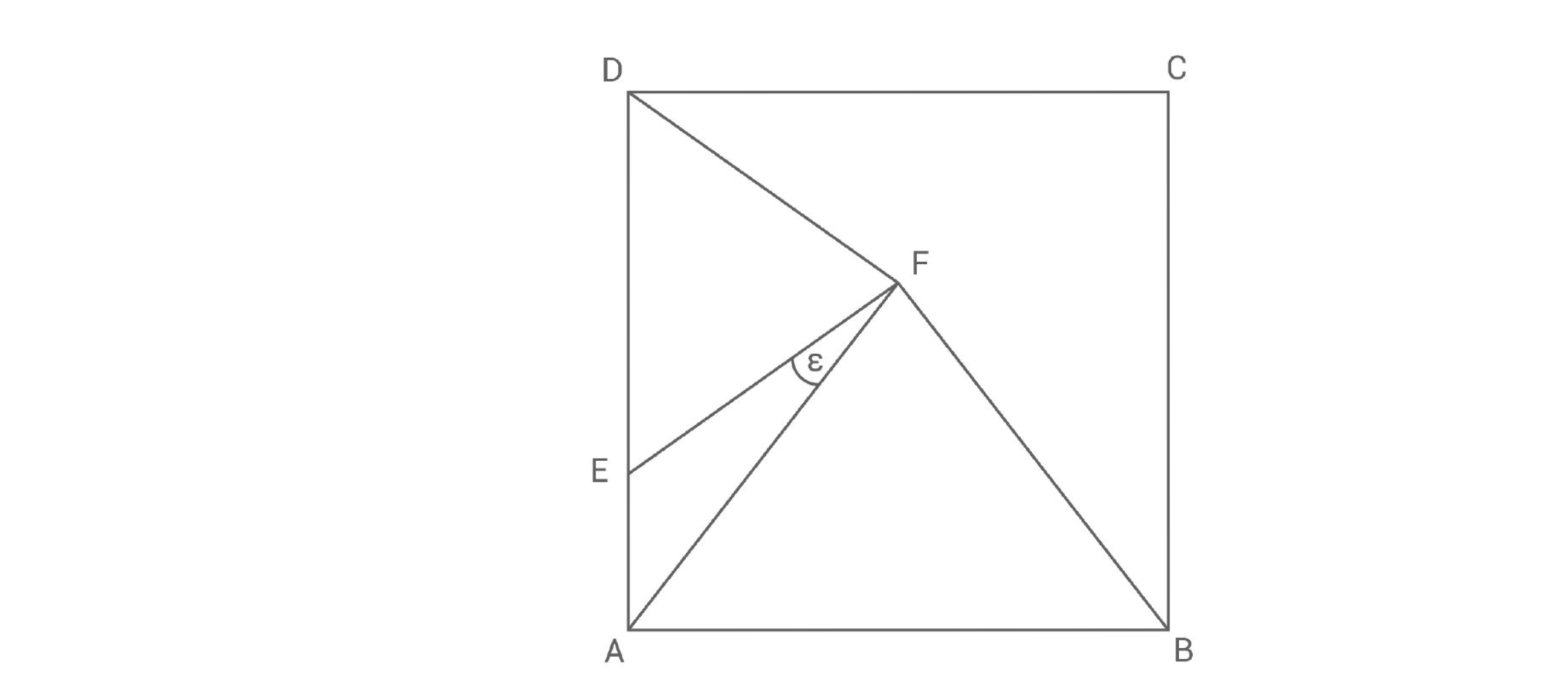
Berechnen des Winkels $ϵ$

$\mathrm{ϵ}=\sphericalangle \mathrm{A}\mathrm{F}\mathrm{W}-\sphericalangle \mathrm{E}\mathrm{F}\mathrm{W}$

$\cos \left(\sphericalangle \mathrm{A}\mathrm{F}\mathrm{W}\right)={\displaystyle \frac{\overline{\mathrm{F}\mathrm{W}}}{\overline{\mathrm{A}\mathrm{F}}}}\Rightarrow \cos \left(\sphericalangle \mathrm{A}\mathrm{F}\mathrm{W}\right)={\displaystyle \frac{7}{12}}$

$\cos \left(\sphericalangle \mathrm{A}\mathrm{F}\mathrm{W}\right)=\mathrm{0,5833}$

$\sphericalangle \mathrm{A}\mathrm{F}\mathrm{W}=\mathrm{54,3}°$

$\tan \left(\sphericalangle \mathrm{E}\mathrm{F}\mathrm{W}\right)={\displaystyle \frac{\overline{\mathrm{E}\mathrm{W}}}{\overline{\mathrm{F}\mathrm{W}}}}\Rightarrow \mathrm{t}\mathrm{a}\mathrm{n}\left(\sphericalangle \mathrm{E}\mathrm{F}\mathrm{W}\right)={\displaystyle \frac{\mathrm{4,25}}{7}}$

$\tan \left(\sphericalangle \mathrm{E}\mathrm{F}\mathrm{W}\right)=\mathrm{0,6071}$

$\sphericalangle \mathrm{E}\mathrm{F}\mathrm{W}=\mathrm{31,3}°$

$\mathrm{ϵ}=\mathrm{54,3}°-\mathrm{31,3}°$

$\mathrm{ϵ}=23°$

Der Winkel $\mathrm{ϵ}$ beträgt $23°$.

Aufgabenteil b.)

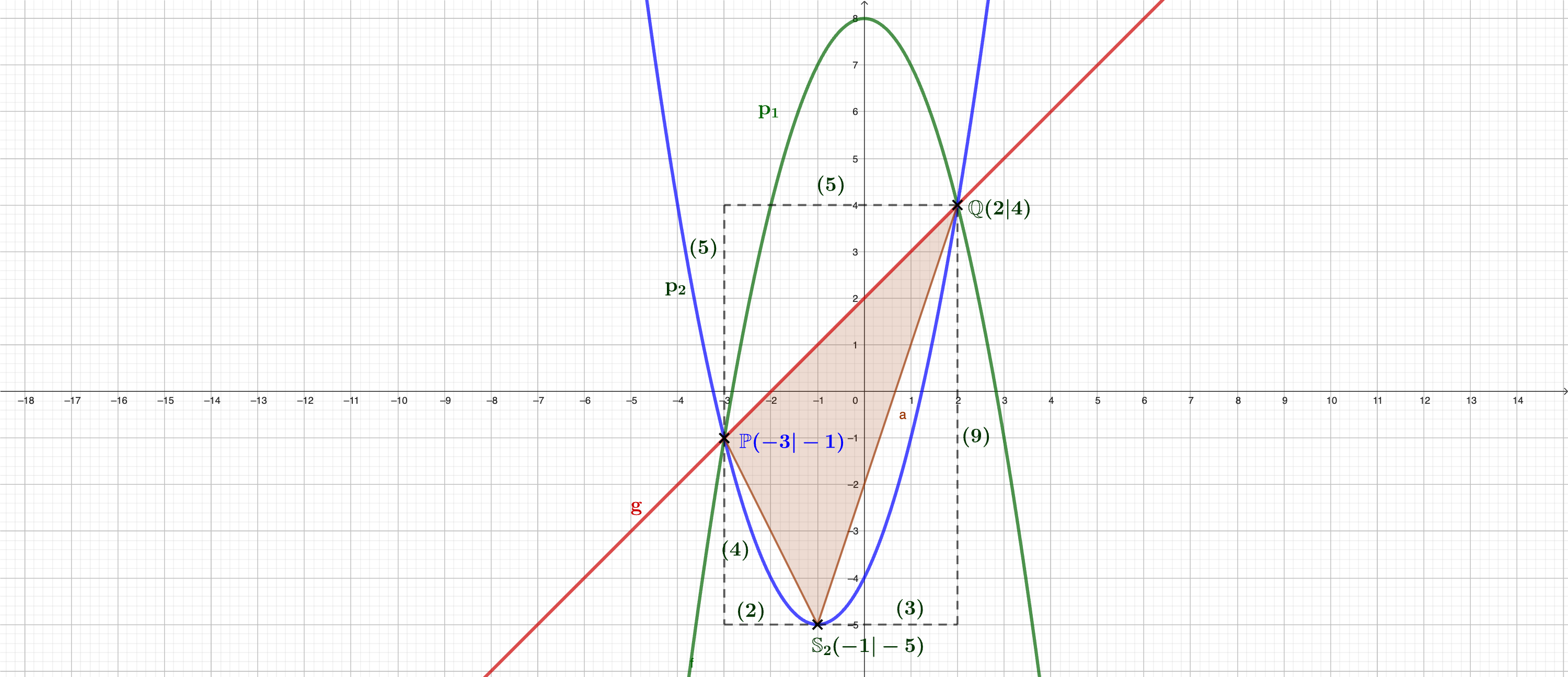
Berechnen der Koordinaten der Schnittpunkte $\text{𝐏}$ und $\text{𝐐}$

Gleichsetzen von $\mathrm{g}:\mathrm{y}=\mathrm{x}+2$ und ${\mathrm{p}}_1:\mathrm{y}=-{\mathrm{x}}^2+8$

Wir setzen ${\mathrm{x}}_1$ und ${\mathrm{x}}_2$ in die Funktionsgleichung der Geraden$\text{𝐠}$ein und berechnen ${\mathrm{y}}_1$ und ${\mathrm{y}}_2$.

${\mathrm{y}}_1=1\cdot (-3)+2$

${\mathrm{y}}_1=-1$

${\mathrm{y}}_2=1\cdot (2)+2$

${\mathrm{y}}_2=4$

Die Koordinaten der Schnittpunkte sind:

$P(-3|-1)Q(2|4)$

Berechnen der Koordinaten des Scheitelpunkts ${\mathrm{S}}_2$ von ${\mathrm{p}}_2$.

Aufstellen der Funktionsgleichung der Parabel ${\mathrm{p}}_2$.

Die allgemeine Form einer quadratischen Funktion lautet:

$\mathrm{f}\left(\mathrm{x}\right)={\mathrm{a}\mathrm{x}}^2+\mathrm{b}\mathrm{x}+\mathrm{c}$

Der Öffnungsfaktor ist $\mathrm{a}=1$, da es sich um eine nach oben geöffnete Normalparabel handelt.

Einsetzen der Koordinaten von $P$ und $Q$ in die allgemeine Form.

$\mathrm{I}(\mathrm{P}):(-3{)}^2-3\mathrm{b}+\mathrm{c}=-1\Rightarrow \mathrm{c}=3\mathrm{b}-10$

$\mathrm{I}\mathrm{I}(\mathrm{Q}):(2{)}^2+2\mathrm{b}+\mathrm{c}=4\Rightarrow \mathrm{c}=-2\mathrm{b}$

Gleichsetzen.

$3\mathrm{b}-10=-2\mathrm{b}$

$5\mathrm{b}=10\Rightarrow \mathrm{b}=2$

eingesetzt in $\mathrm{II}$

$\mathrm{c}=-2\cdot 2\Rightarrow \mathrm{c}=-4$

${\mathrm{p}}_2:\mathrm{y}={\mathrm{x}}^2+2\mathrm{x}-4$

Aufstellen der Scheitelform.

Die Scheitelform einer quadratischen Funktionsgleichung lautet:

$\mathrm{f}(\mathrm{x})=\mathrm{a}(\mathrm{x}-{\mathrm{x}}_{\mathrm{s}}{)}^2+{\mathrm{y}}_{\mathrm{s}}$ $(\mathrm{a}=1)$ siehe oben.

${\mathrm{p}}_2:\mathrm{y}=(\mathrm{x}+1{)}^2-1-4$

Scheitelform der Funktionsgleichung der Parabel ${\mathrm{p}}_2$.

${\mathrm{p}}_2:\mathrm{y}=(\mathrm{x}+1{)}^2-5$

Koordinaten des Scheitelpunkts: ${\mathrm{S}}_2(-1|-5)$

Überprüfen von Robins Behauptung.

Ist Robins Behauptung richtig, dann muss für das farbige Dreieck der Satz des Pythagoras gelten, nämlich:

${\overline{{\mathrm{S}}_2\mathrm{Q}}}^2={\overline{\mathrm{Q}\mathrm{P}}}^2+{\overline{\mathrm{P}{\mathrm{S}}_2}}^2$(siehe Skizze)

$\overline{{\mathrm{S}}_2\mathrm{Q}}=\sqrt{3^2+9^2}\Rightarrow \overline{{\mathrm{S}}_2\mathrm{Q}}=\sqrt{90}\mathrm{L}\mathrm{E}$

$\overline{\mathrm{Q}\mathrm{P}}=\sqrt{5^2+5^2}\Rightarrow \overline{\mathrm{Q}\mathrm{P}}=\sqrt{50}\mathrm{L}\mathrm{E}$

$\overline{\mathrm{P}{\mathrm{S}}_2}=\sqrt{4^2+2^2}\Rightarrow \overline{\mathrm{P}{\mathrm{S}}_2}=\sqrt{20}\mathrm{L}\mathrm{E}$

Prüfen, ob der Satz des Pythagoras gilt.

${\left(\sqrt{90}\right)}^2={\left(\sqrt{50}\right)}^2+{\left(\sqrt{20}\right)}^2$

$90\ne 50+20$

$90\ne 70$

Der Satz des Pythagoras gilt nicht in diesem Dreieck, also ist das Dreieck nicht rechtwinklig.

Robin hat nicht Recht!