Wahlteil B

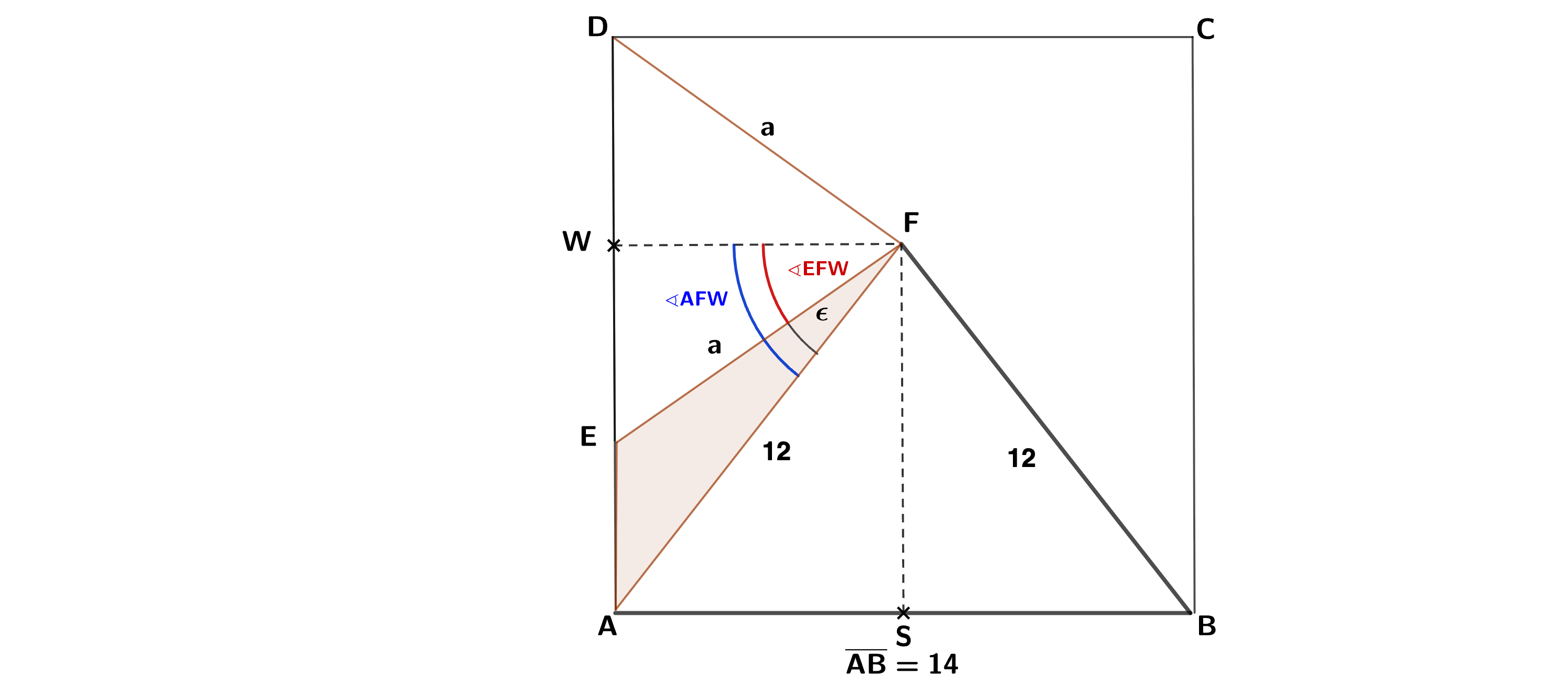
a) Im Quadrat $\text{ABCD}$ liegen die beiden gleichschenkligen Dreiecke $\text{ABF}$ und $\text{DEF}$.

Es gilt:

$\overline{\mathrm{A}\mathrm{B}}=\mathrm{14,0}\text{ cm}$

$\overline{\mathrm{A}\mathrm{F}}=\mathrm{12,0}\text{ cm}$

$\overline{\mathrm{A}\mathrm{F}}=\overline{\mathrm{B}\mathrm{F}}$

$\overline{\mathrm{E}\mathrm{F}}=\overline{\mathrm{D}\mathrm{F}}$

• Berechne den Flächeninhalt des Dreiecks $\mathrm{AFE}$.

• Berechne den Winkel $ϵ$.

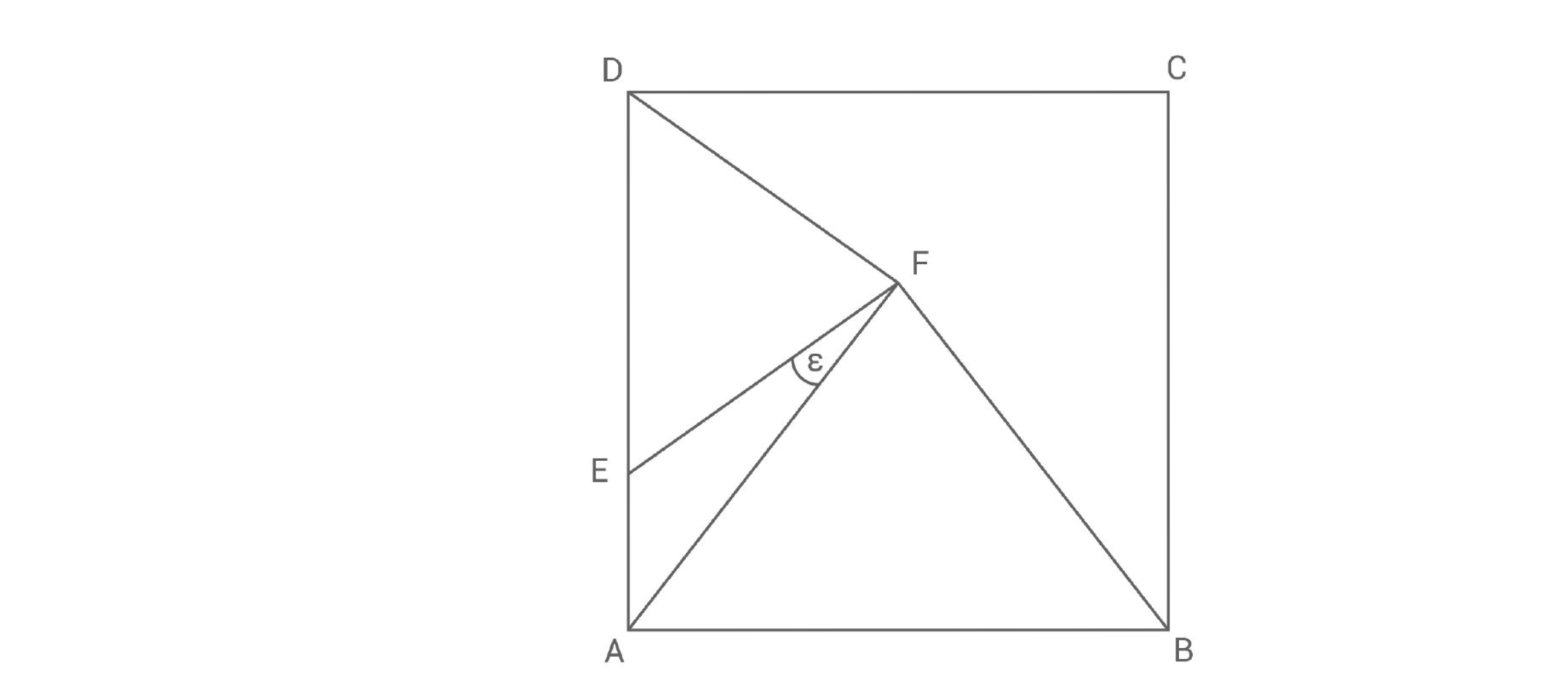
(5 Pkt.)

b) Die Gerade $\text{g}$ hat die Funktionsgleichung $\mathrm{y}=\mathrm{x}+2$.

Die Parabel ${\mathrm{p}}_1$ hat die Funktionsgleichung $\mathrm{y}=-{\mathrm{x}}^2+8$. Die Parabel ${\mathrm{p}}_1$ schneidet die Gerade $\mathrm{g}$ in den Punkten $\text{P}$ und $\text{Q}$.

• Berechne die Koordinaten der Schnittpunkte $\text{P}$ und $\text{Q}$.

Durch die beiden Schnittpunkte $\text{P}$ und $\text{Q}$ verläuft die verschobene nach oben geöffnete

Normalparabel $p_2$.

• Berechne die Koordinaten des Scheitelpunkts ${\mathrm{S}}_2$ von ${\mathrm{p}}_2$.

Robin behauptet: „Das Dreieck mit den Punkten $\mathrm{P},\mathrm{Q}$ und ${\mathrm{S}}_2$ ist rechtwinklig.“

• Hat Robin Recht? Begründe deine Antwort rechnerisch.

(5 Pkt.)

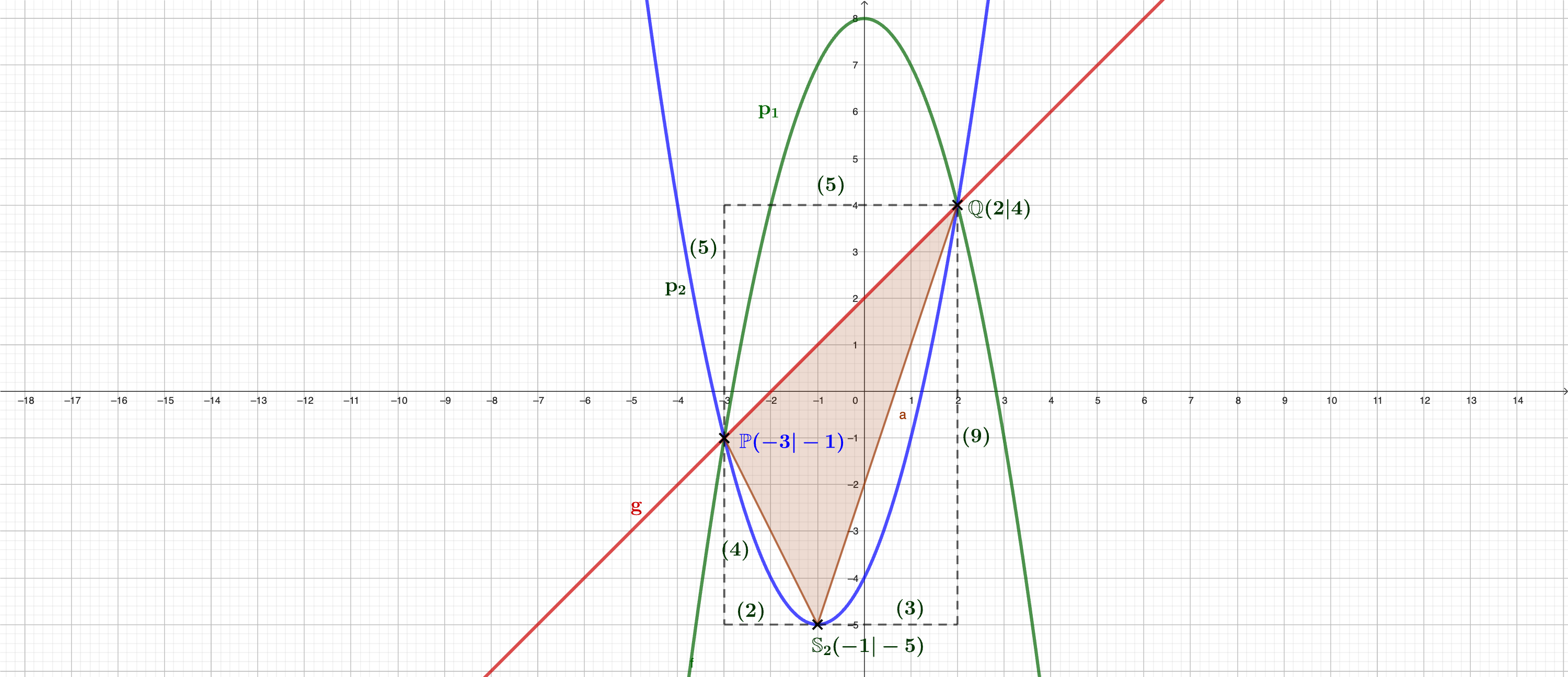
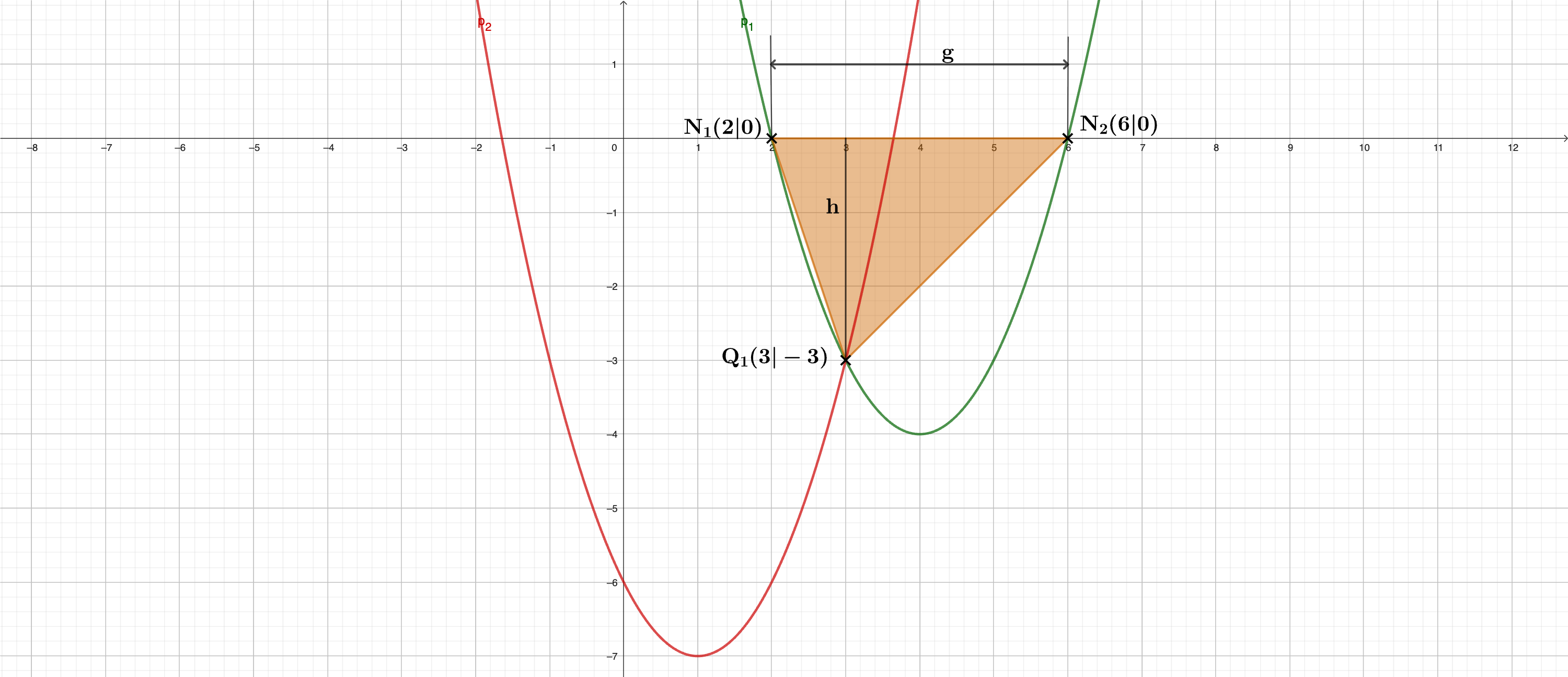
a) Das Schaubild zeigt Ausschnitte der verschobenen Normalparabel ${\mathrm{p}}_1$ und der nach

unten geöffneten Parabel ${\mathrm{p}}_2$.

• Bestimme die Funktionsgleichungen der beiden Parabeln. Entnimm dazu geeignete Werte aus dem Schaubild.

Die Gerade $g$ verläuft durch die beiden

Scheitelpunkte ${\mathrm{S}}_1$ und ${\mathrm{S}}_2$.

• Berechne die Funktionsgleichung von $\text{g}$.

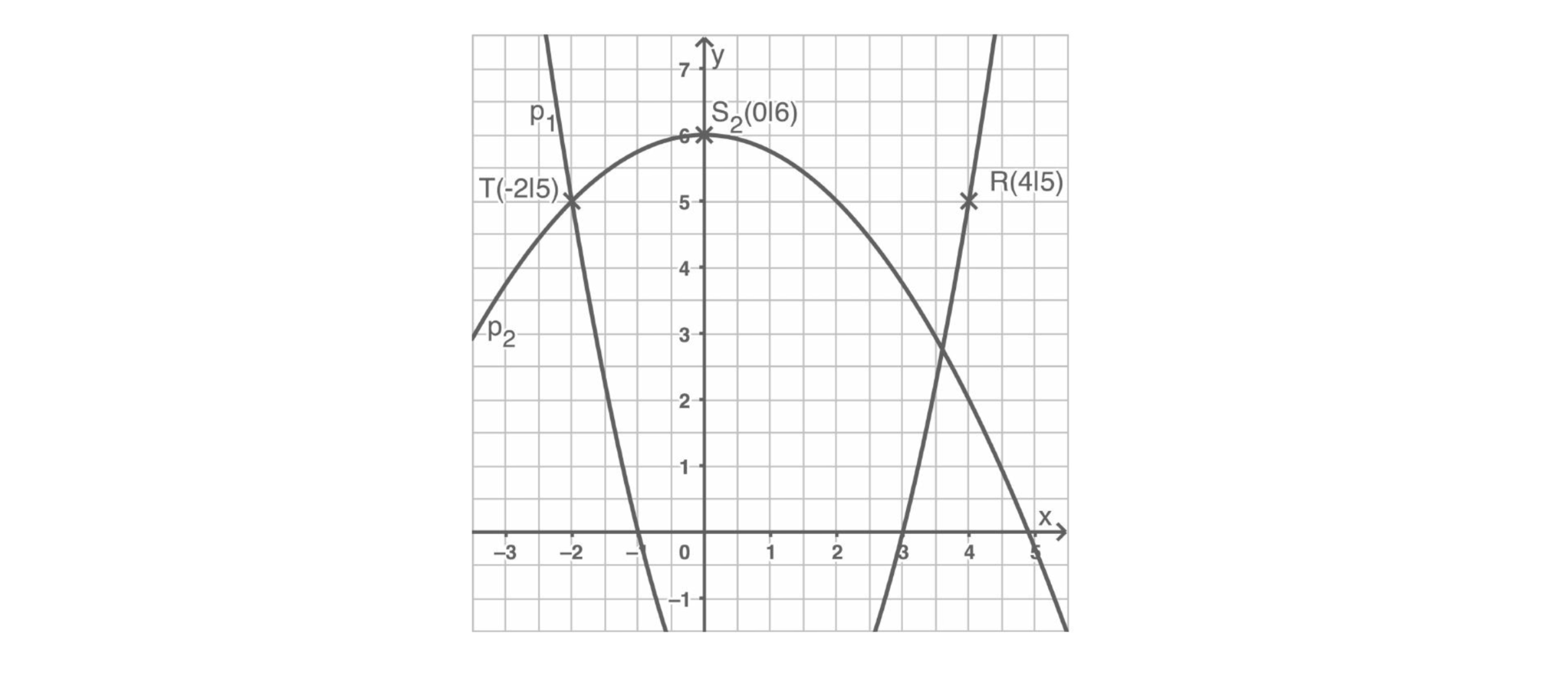
Die Gerade $\text{h}$ verläuft senkrecht zu $\text{g}$ und geht durch den Punkt $\mathrm{R}(4|5)$.

• Berechne die Funktionsgleichung von $\text{h}$.

• Gib die Funktionsgleichung einer weiteren verschobenen nach oben geöffneten Normalparabel ${\mathrm{p}}_3$ an, die keine Punkte mit ${\mathrm{p}}_1$ und ${\mathrm{p}}_2$ gemeinsam hat.

(5 Pkt.)

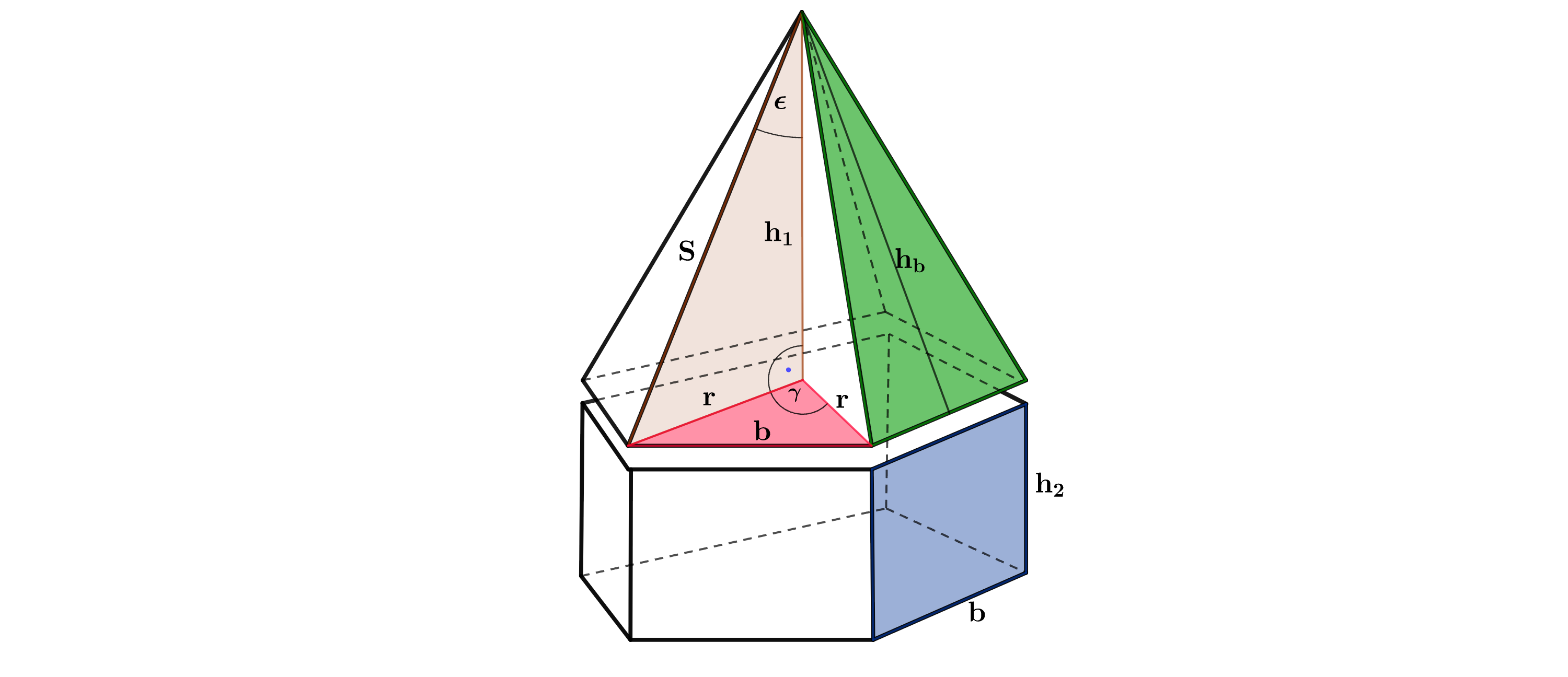
b) Ein zusammengesetzter Körper besteht aus einem regelmäßigen

Fünfecksprisma mit aufgesetzter regelmäßiger fünfseitiger Pyramide.

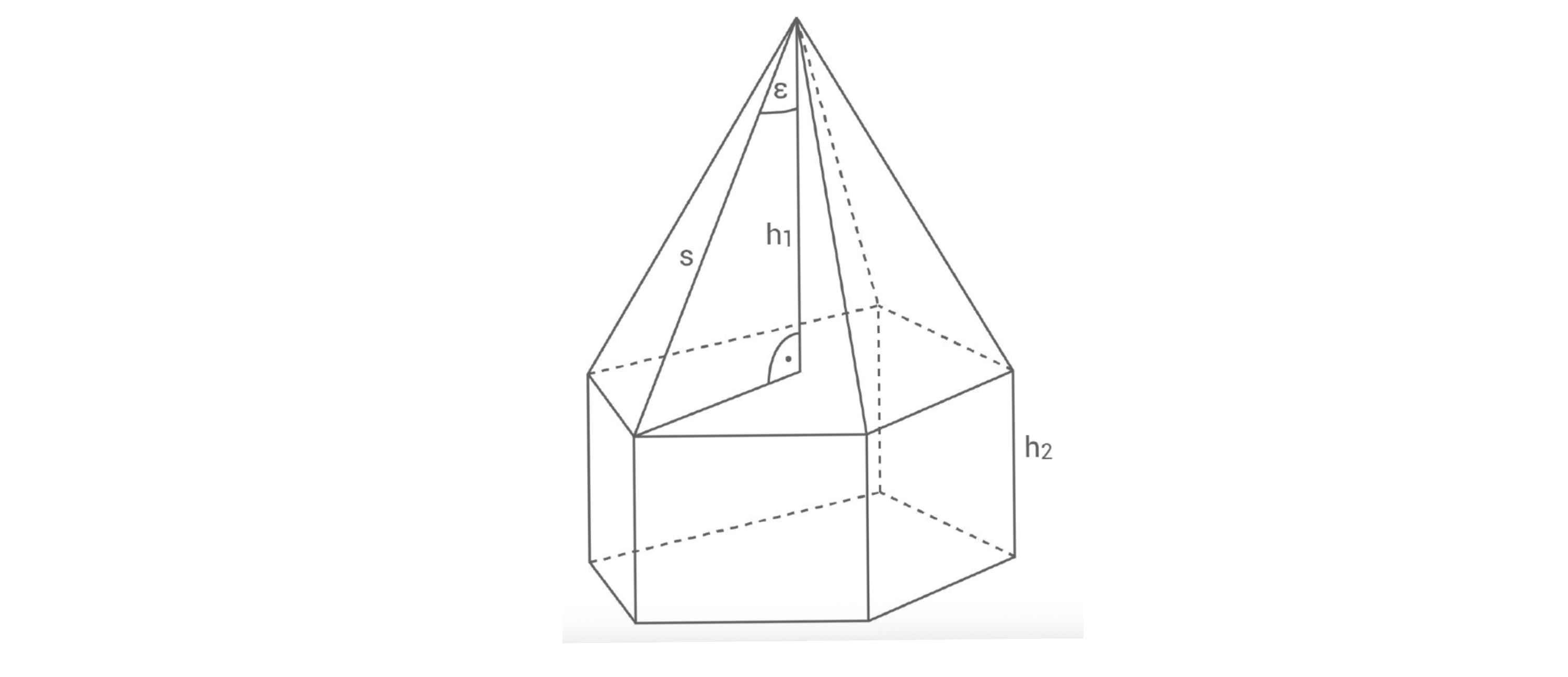
Es gilt:

$\mathrm{s}=\mathrm{12,6}\text{ cm}$

$\epsilon =\mathrm{33,0}°$

${\mathrm{h}}_2=\mathrm{5,6}\text{ cm}\text{ (Höhe Prisma)}$

Berechne den Oberflächeninhalt des zusammengesetzten Körpers.

(5 Pkt.)

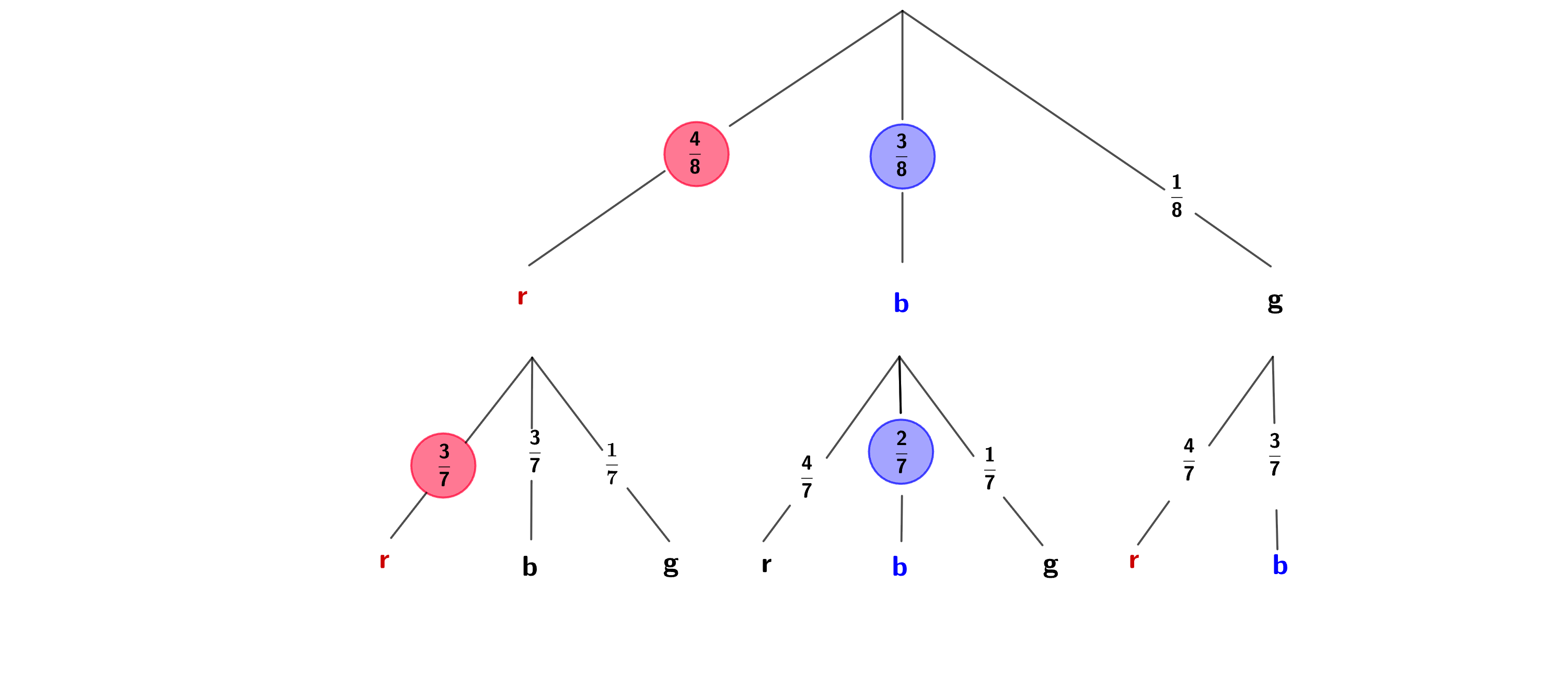
a) In einem Gefäß liegen acht Kugeln, die rot, blau und grün gefärbt sind.

Es werden zwei Kugeln ohne Zurücklegen gezogen.

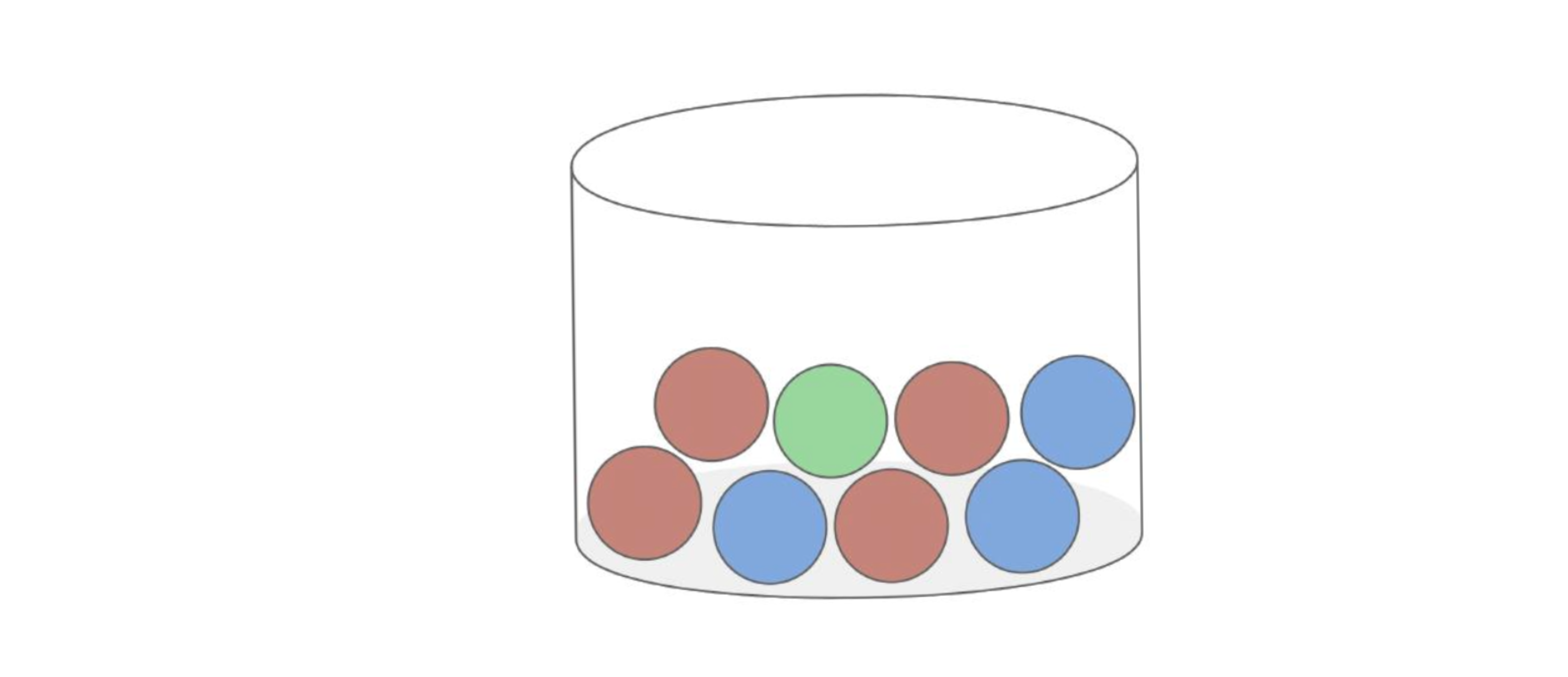
• Wie groß ist die Wahrscheinlichkeit, zwei gleichfarbige Kugeln zu ziehen?

Die Kugeln werden für ein Gewinnspiel eingesetzt. Dazu wird folgender Gewinnplan geprüft.

• Berechne den Erwartungswert.

Einsatz: 2,50 € pro Spiel

Der Veranstalter des Gewinnspiels möchte seinen Gewinn pro Spiel auf lange Sicht verdoppeln.

• Wie hoch müsste dann der Gewinn für „eine grüne und eine blaue Kugel" sein, wenn alles $$andere unverändert bleibt?

(5 Pkt.)

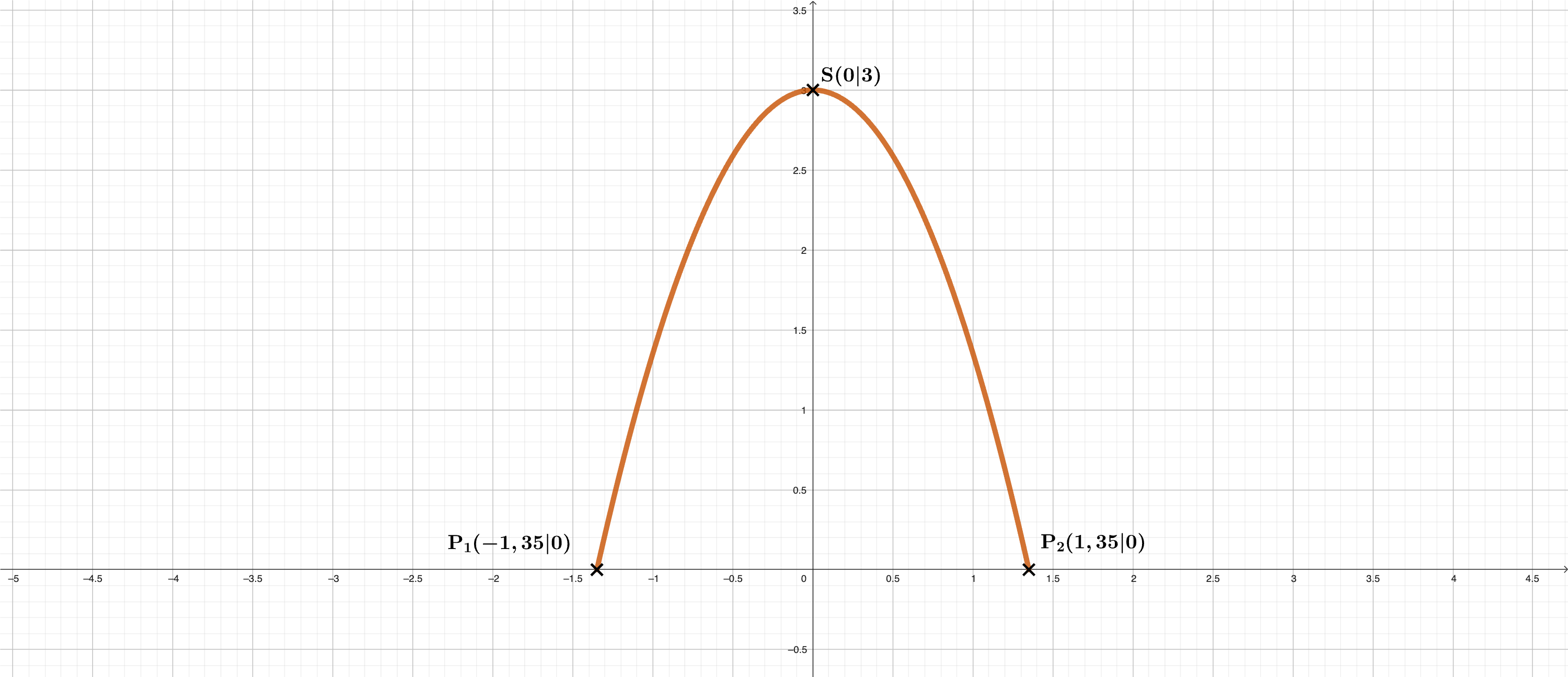
b) Das Foto zeigt ein „Tiny House". Die Vorderseite des Hauses ist annähernd parabelförmig. Die maximale Höhe des Hauses beträgt $\mathrm{3,00}\mathrm{m}$.

Am Boden ist es $\mathrm{2,70}\mathrm{m}$ breit.

• Berechne eine mögliche Funktionsgleichung für die parabelförmige Außenkante des Hauses.

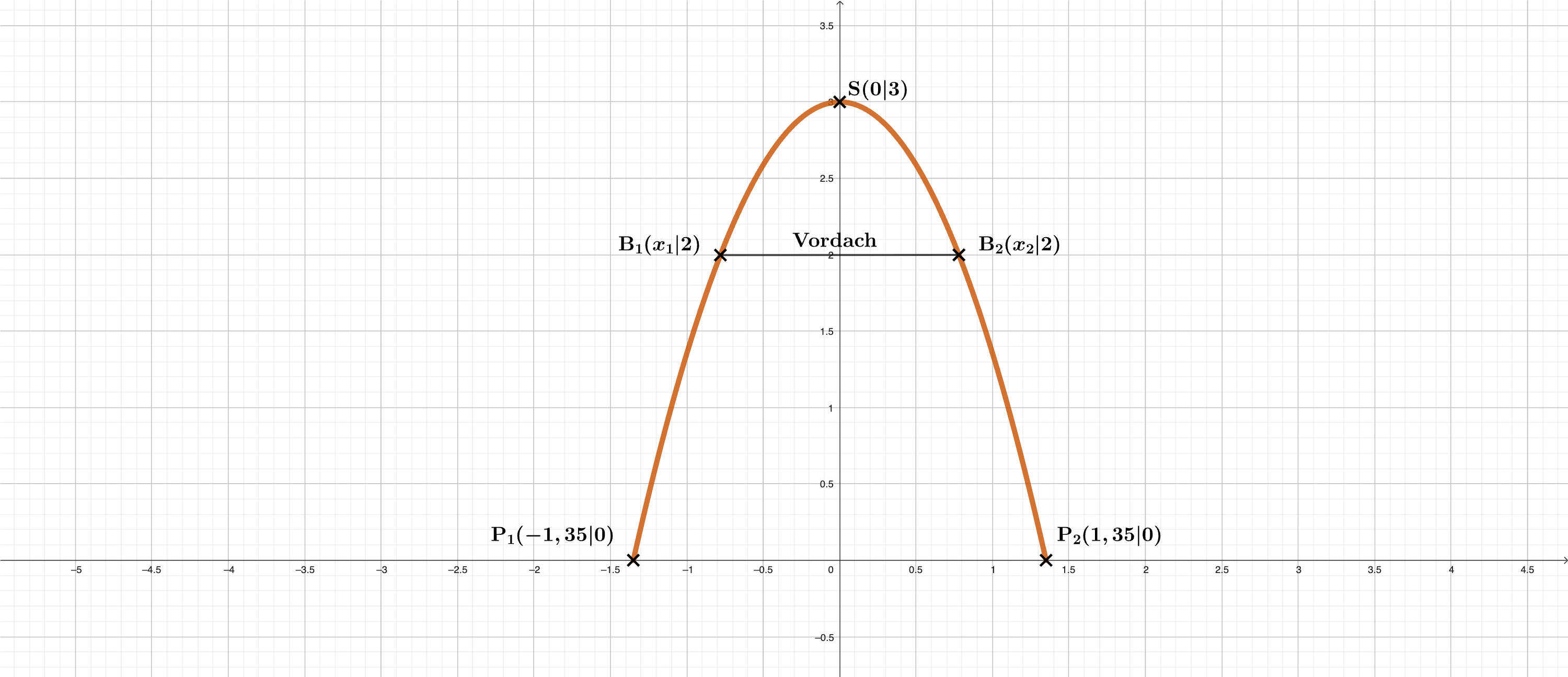
Die $\mathrm{2,00}\mathrm{m}$ hohe Eingangstür befindet sich mittig auf der Vorderseite des Hauses.

Am oberen Ende der Eingangstür befindet sich ein Vordach, das von Außenkante

zu Außenkante reicht.

• Berechne die Länge dieses Vordachs.

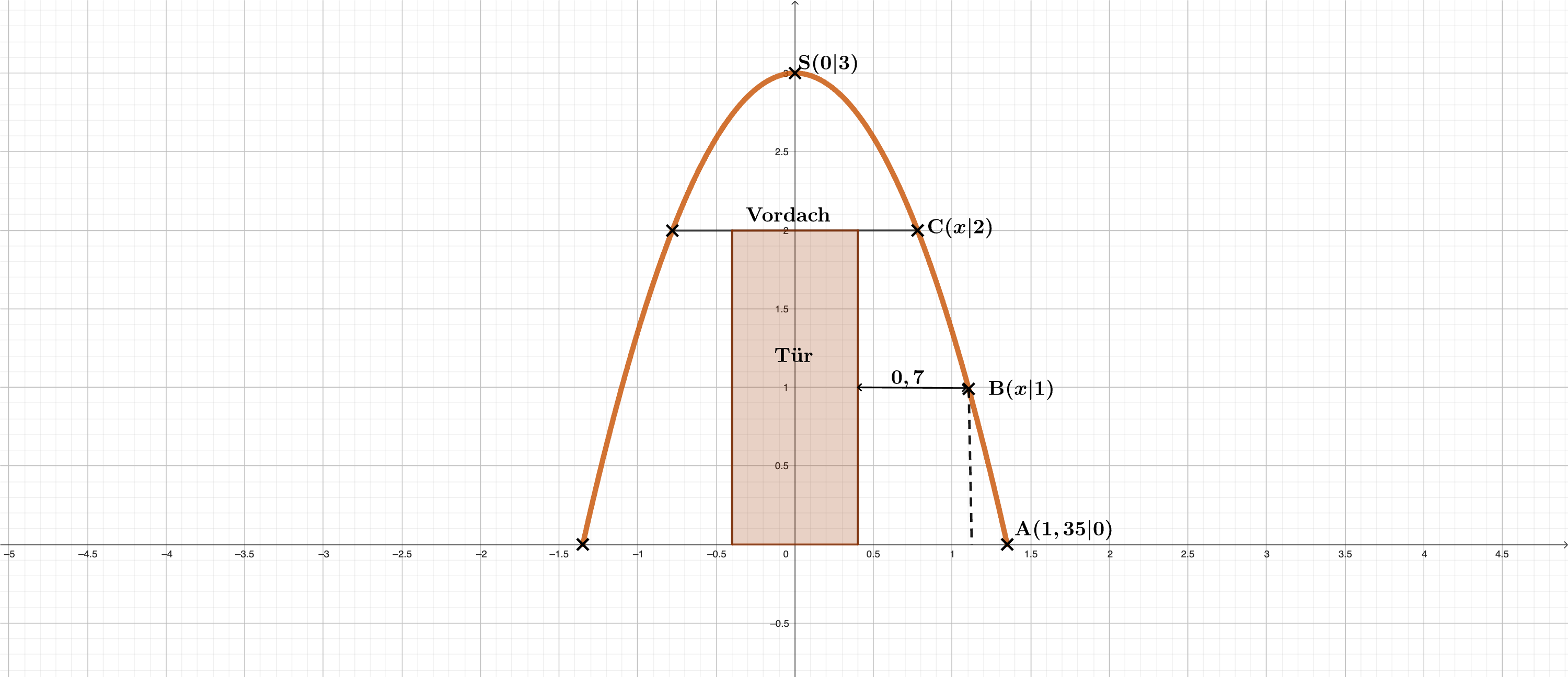
In $\mathrm{1,00}\mathrm{m}$ Höhe hat der Türrahmen eine waagrechte Entfernung von $\mathrm{0,70}\text{ m}$ zu den Außenkanten.

• Berechne den Flächeninhalt der Tür.

(5 Pkt.)

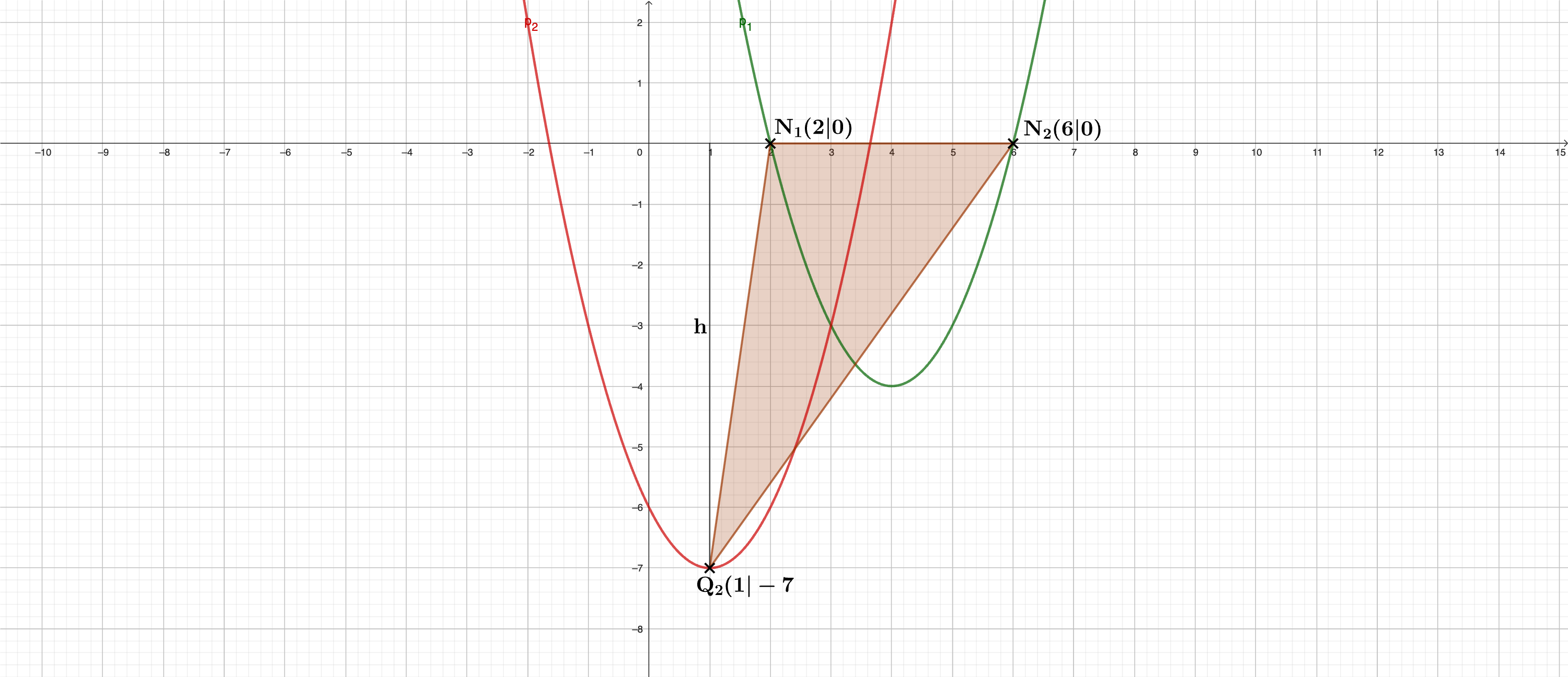
a) Die Parabel ${\mathrm{p}}_1$ hat die Funktionsgleichung $\mathrm{y}={\mathrm{x}}^2-8\mathrm{x}+12$.

Die verschobene nach oben geöffnete Normalparabel ${\mathrm{p}}_2$ hat den Scheitelpunkt ${\mathrm{S}}_2(1|-7)$.

• Berechne die Koordinaten des Schnittpunkts ${\mathrm{Q}}_1$ der beiden Parabeln ${\mathrm{p}}_1$ und ${\mathrm{p}}_2$.

Die Parabel ${\mathrm{p}}_1$ schneidet die $\text{x}$-Achse in den Punkten ${\mathrm{N}}_1$ und ${\mathrm{N}}_2$.

• Berechne die Koordinaten von ${\mathrm{N}}_1$ und ${\mathrm{N}}_2$.

Die Punkte ${\mathrm{N}}_1,{\mathrm{N}}_2$ und ${\mathrm{Q}}_1$ bilden ein Dreieck.

• Berechne den Flächeninhalt des Dreiecks ${\mathrm{N}}_1{\mathrm{Q}}_1{\mathrm{N}}_2$.

Der Punkt ${\mathrm{Q}}_1$ bewegt sich auf der Parabel ${\mathrm{p}}_2$ unterhalb der $\text{x}$-Achse. Dadurch entsteht der

Punkt ${\mathrm{Q}}_2$ und somit das Dreieck ${\mathrm{N}}_1{\mathrm{Q}}_2{\mathrm{N}}_2$.

• Für welche Lage von ${\mathrm{Q}}_2$ wird der Flächeninhalt des Dreiecks am größten?

• Berechne diesen maximalen Flächeninhalt.

(5 Pkt.)

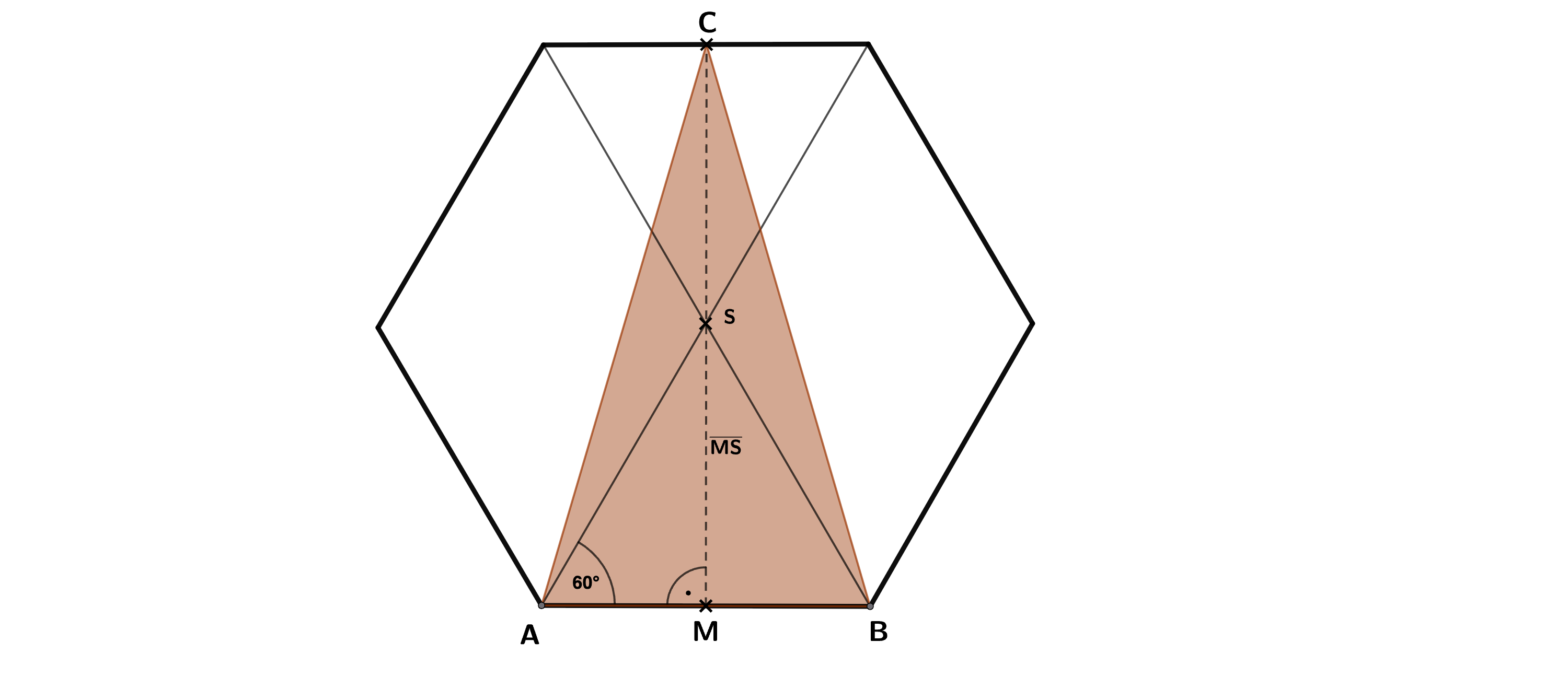
b) Das regelmäßige Sechseck und das gleichschenklige Dreieck $\text{ABC}$ haben die Seite $\overline{\mathrm{A}\mathrm{B}}$

gemeinsam.

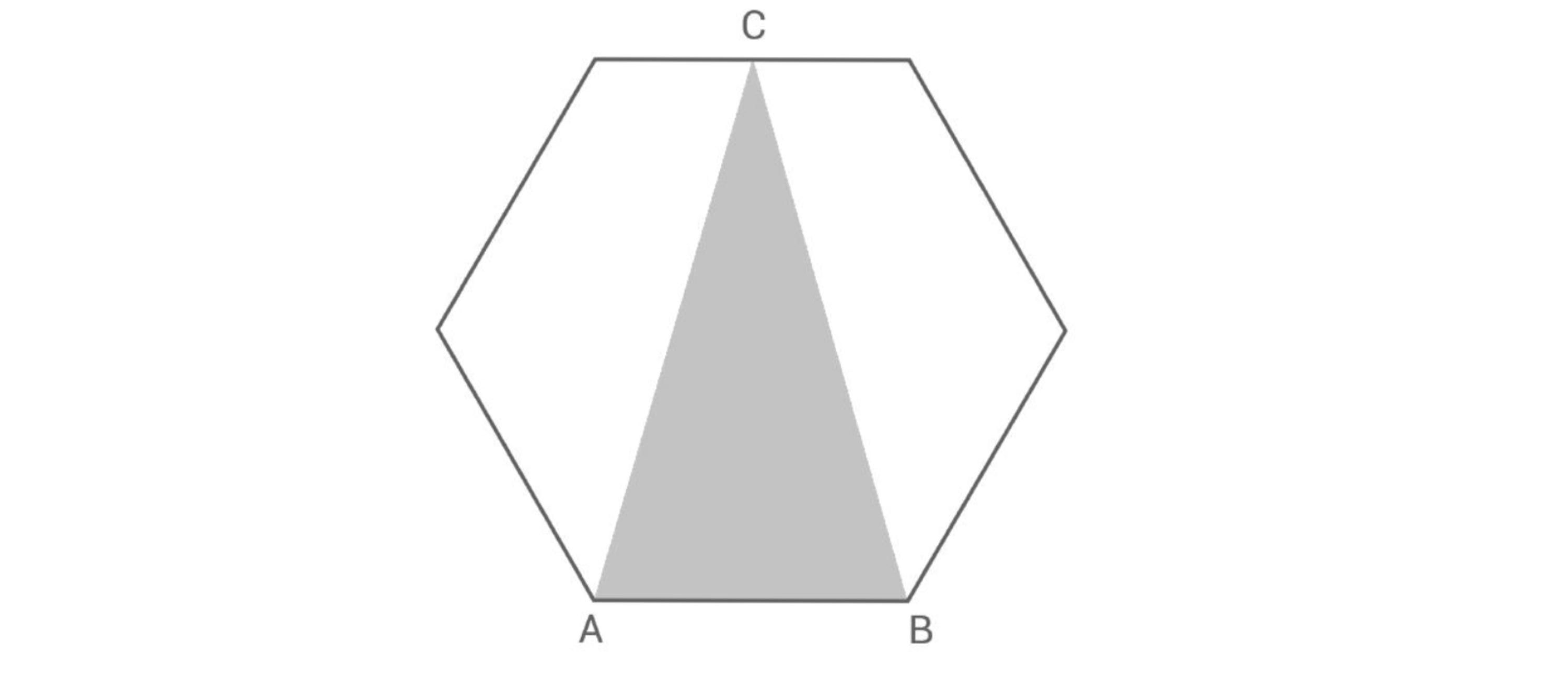
Es gilt: $\overline{\mathrm{A}\mathrm{B}}=\mathrm{12,4}\text{ cm}$

• Berechne den Umfang des Dreiecks $ABC$.

Tom behauptet: „Der Flächeninhalt des Sechsecks ist dreimal so groß wie der Flächeninhalt des Dreiecks $\text{ABC}$."

• Hat Tom Recht? Begründe deine Antwort durch Rechnung oder Argumentation.

(5 Pkt.)