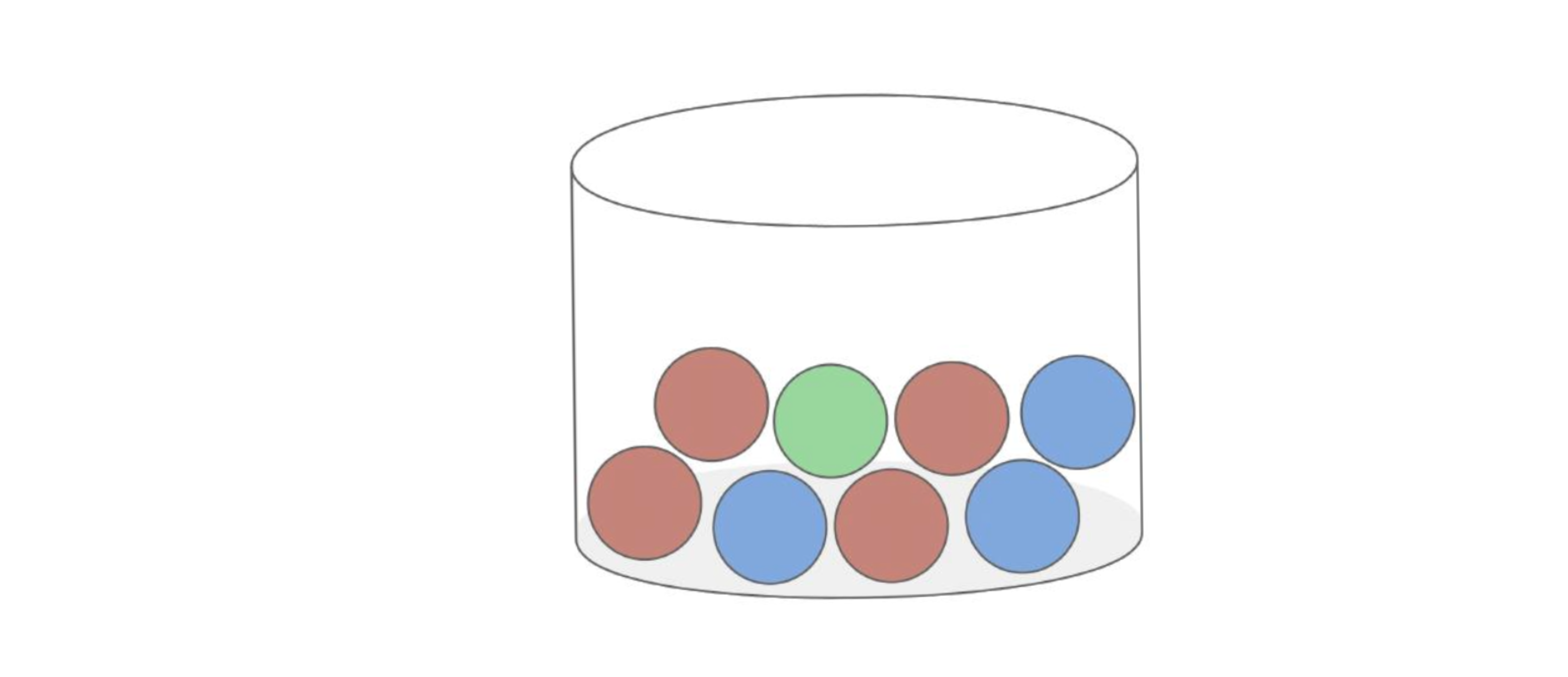
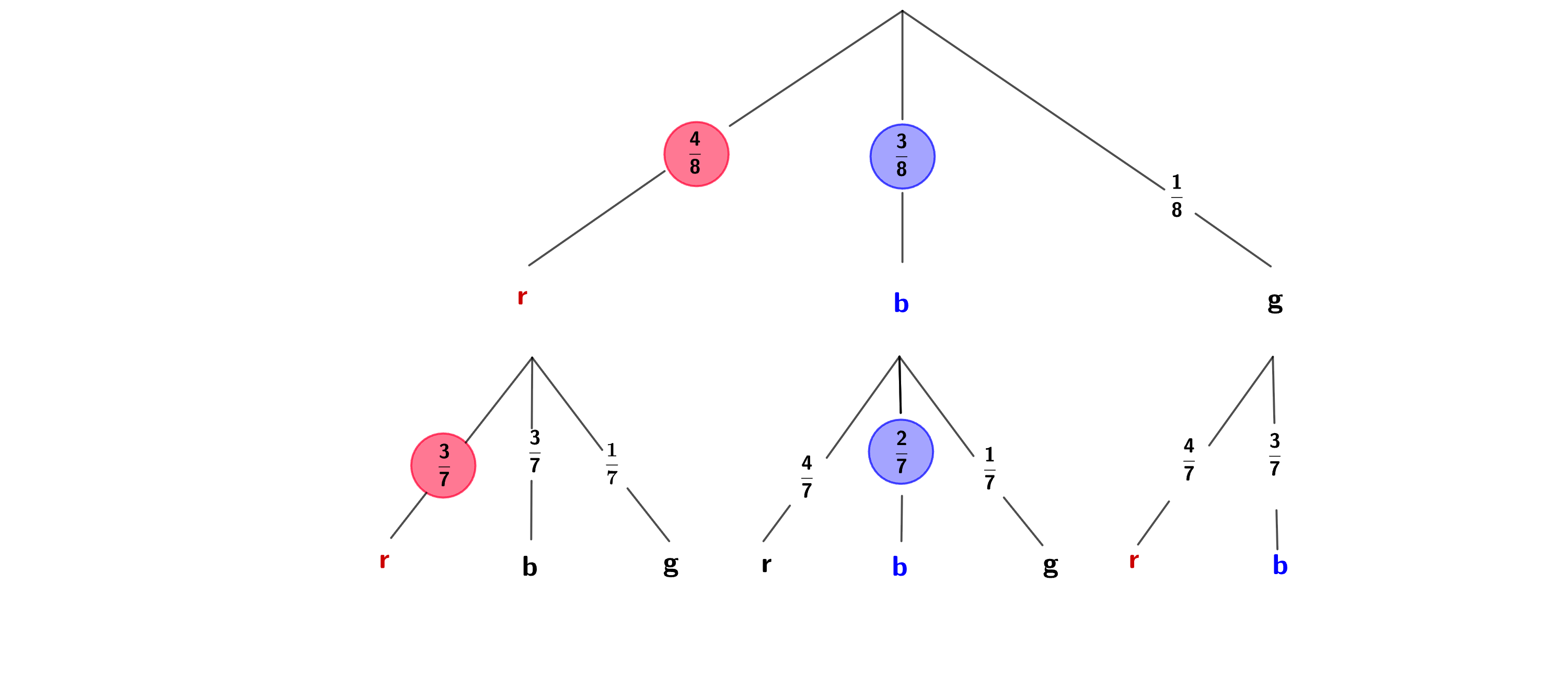
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Aufgabenteil a.)
Berechnen der Wahrscheinlichkeit zwei gleichfarbige Kugeln zu ziehen.
Berechnen der Wahrscheinlichkeit, 2 rote Kugeln zu ziehen:
Anwenden der 1. Pfadregel:
Berechnen der Wahrscheinlichkeit, 2 blaue Kugeln zu ziehen:
Anwenden der 1. Pfadregel:
Wahrscheinlichkeit 2 gleichfarbige Kugeln zu ziehen:
Anwenden der 2. Pfadregel:
Die Wahrscheinlichkeit 2 gleichfarbige Kugeln zu ziehen beträgt:
oder
Berechnen des Erwartungswertes.
Der Erwartungswert berechnet sich nach folgender Formel:
wobei:
Werte
Wahrscheinlichkeiten
Für unsere Aufgabe ergibt sich dann:
Für dieses Glücksspiel gibt es mögliche Ereignisse
zwei gleichfarbige Kugeln: oder
eine grüne und eine blaue Kugel: oder
restliche Möglichkeiten: alle anderen
Wahrscheinlichkeit, zwei gleichfarbige Kugeln zu ziehen:
siehe oben
Wahrscheinlichkeit, eine grüne und eine blaue Kugel zu ziehen:
siehe Baumdiagramm
restliche Möglichkeiten: alle anderen
Es ergeben sich folgende Gewinnwerte:
Gleichfarbige Kugeln, Gewinn:
Grüne und blaue Kugel, Gewinn:
alle anderen:
Der Erwartungswert beträgt:
Berechnen der Änderung des Gewinnplans für Verdopplung des Gewinns für den Veranstalter:
Bei einer Verdoppelung des Gewinns für den Veranstalter verdoppelt sich der Erwartungswert .
Verdoppelter Erwartungswert:
Gewinn für „eine grüne und eine blaue Kugel“ :
Einsetzen der Werte in die Formel:
Berechnen von x |
| ↓ |
| | | |
| ↓ | multiplizieren |
| | | |
| ↓ | zusammenfassen |
| | | |
| ↓ | addieren |
| | | |
| ↓ | dividieren, Seiten tauschen |
| | | |
Will der Veranstalter seinen Gewinn verdoppeln, muss der Gewinn für eine "grüne und eine blaue Kugel", betragen.
Aufgabenteil b.)
Berechnen einer möglichen Funktionsgleichung für die parabelförmige Außenkante des Hauses.
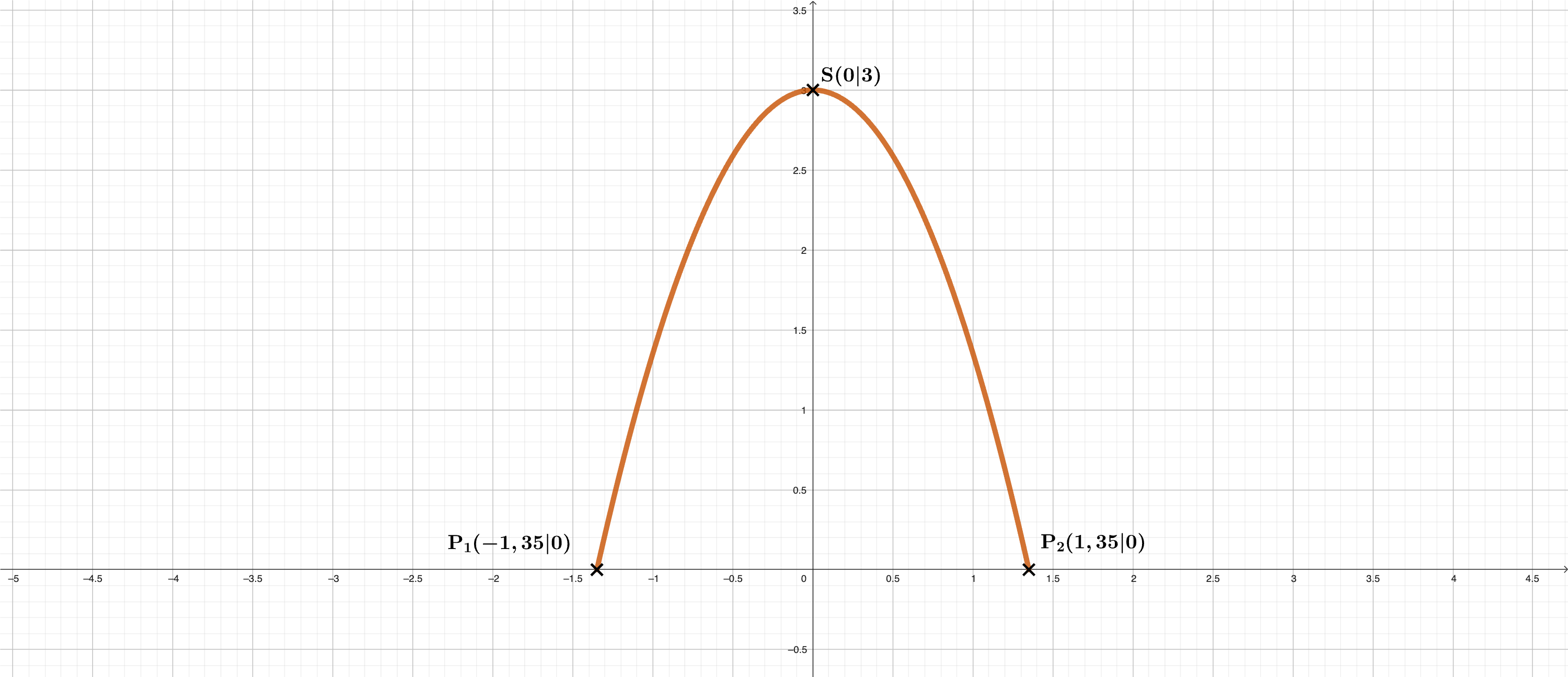
Bild 1
Wir legen den Scheitelpunkt der Parabel z. B. auf die und erhalten damit die folgenden Punkte:
Aufstellen der Funktionsgleichung der Parabel mithilfe der Scheitelform.
Die allgemeine Scheitelform lautet:
Einsetzen der Koordinaten der Punkte und in die allgemeine Scheitelform.
Eine mögliche Funktionsgleichung der Parabel lautet dann:
Berechnen der Länge des Vordaches.
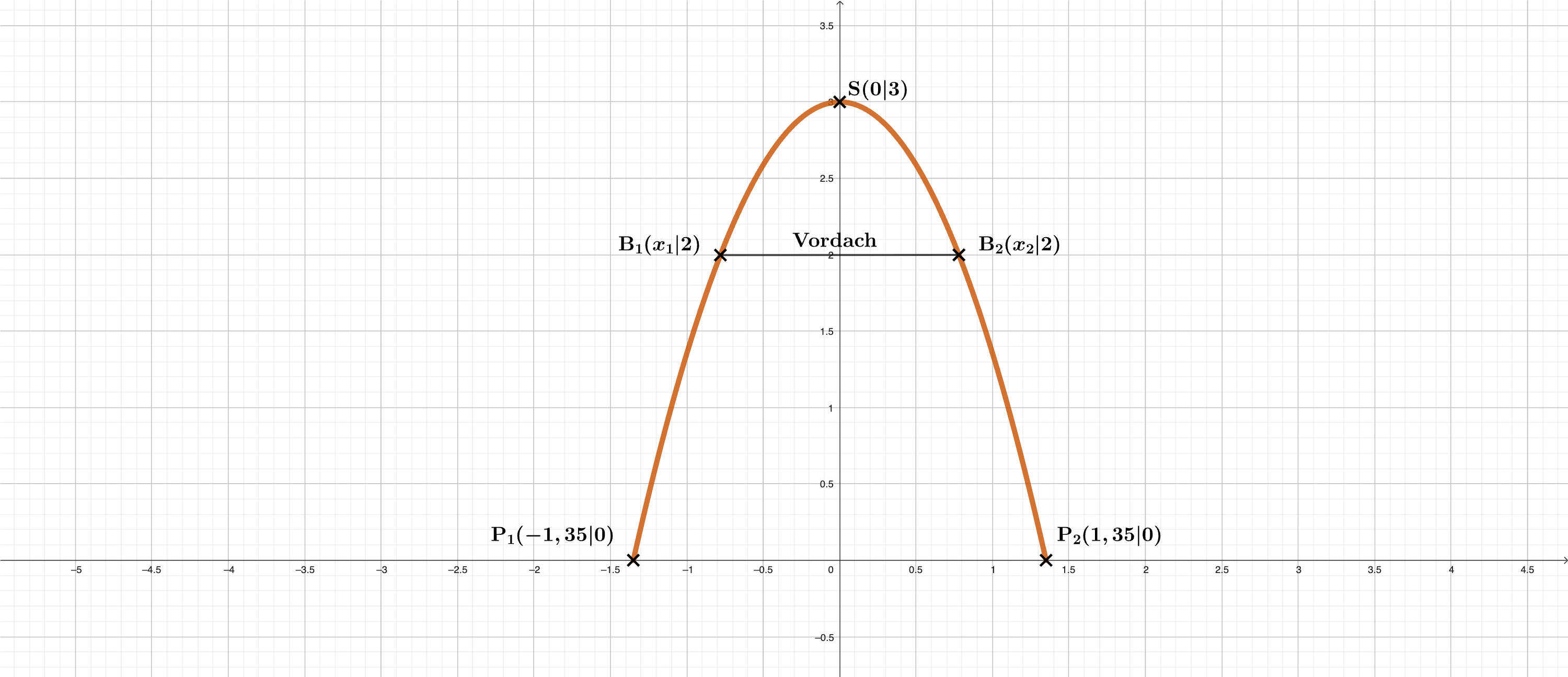
Bild 2
Das Vordach befindet sich in einer Höhe von , d. h. der Funktionswert
berechnen von x |
| ↓ |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | dividieren |
| | | |
| | | |
| ↓ | Quadratwurzel |
| | | |
Die Länge des Vordachs beträgt: .
Berechnen des Flächeninhalts der Tür.
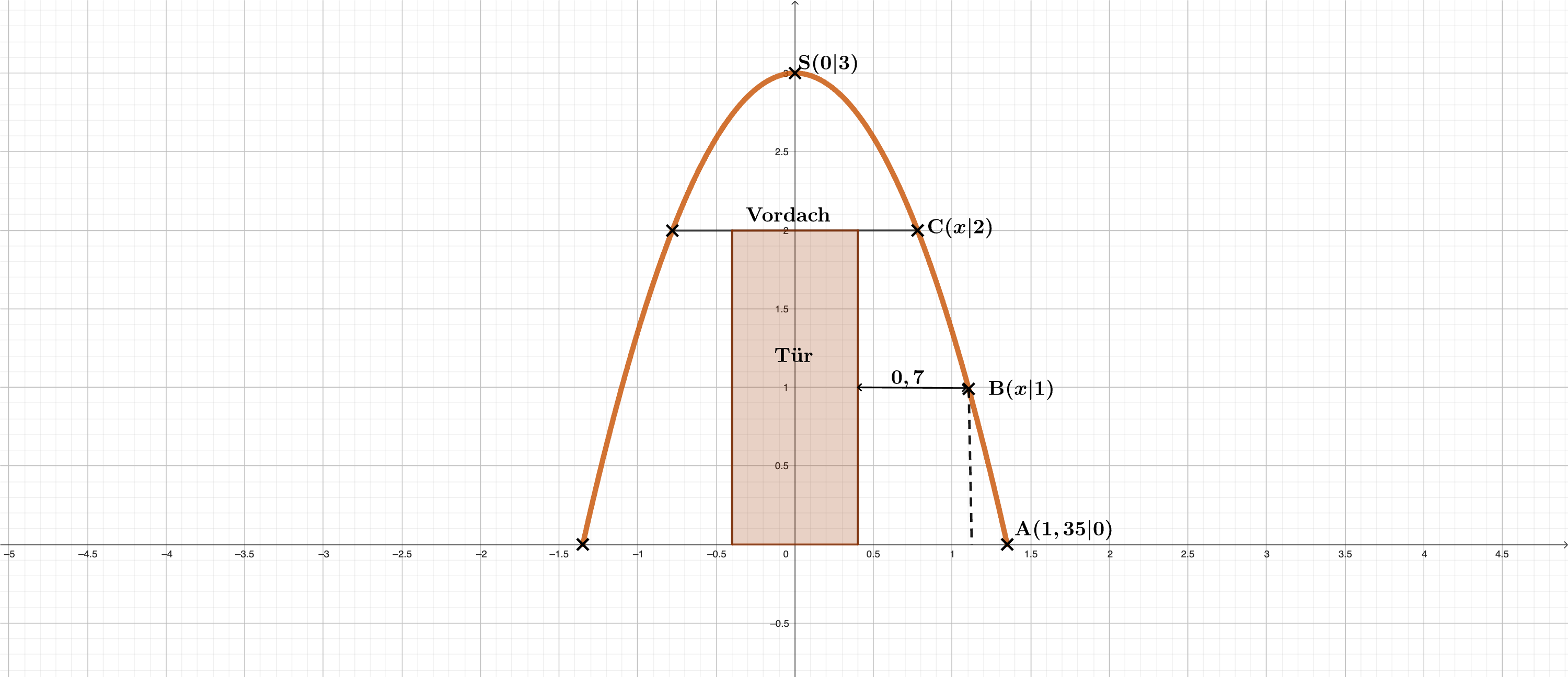
Bild 3
Berechnen der Breite der Tür.
Einsetzen der -Koordinate des Punktes in die Funktionsgleichung und berechnen von .
berechnen von x |
| ↓ |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | dividieren |
| | | |
| | | |
| ↓ | Quadratwurzel |
| | | |
Die Breite der Türe berechnet sich dann wie folgt:
(siehe Bild 3)
Der Flächeninhalt der Tür berechnet sich dann wie folgt:
Der Flächeninhalt der Tür beträgt: .