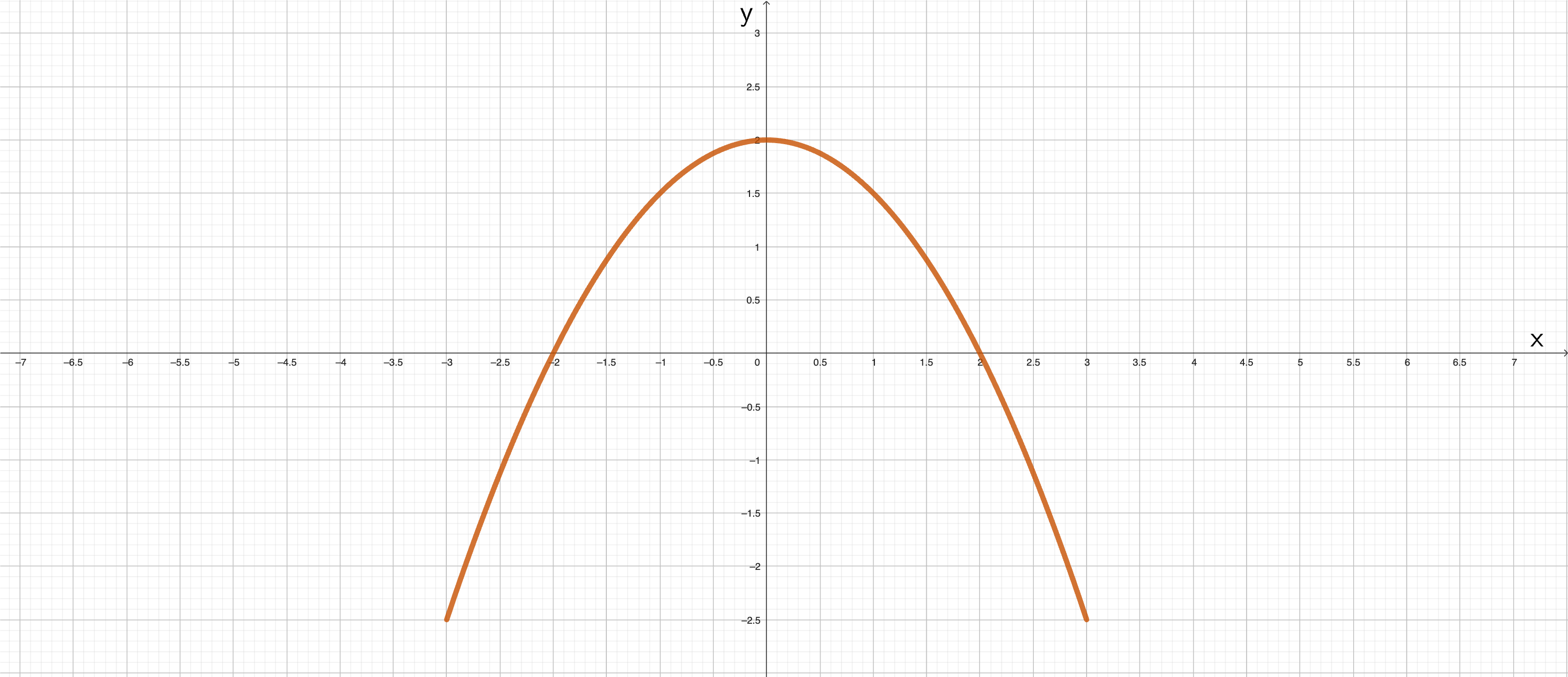
Aufgabenteil a.)

Erstellen der Wertetabelle.

Zeichnen der Parabel in ein Koordinatensystem.

Bestimmen der Funktionsgleichung der gespiegelten Parabel.

Eine Parabel wird an einer Geraden, die parallel zur x-Achse verläuft, gespiegelt, indem man den Funktionsterm mit $(-1)$ multipliziert und anschließend um $\text{𝟐𝐜}$ verschiebt.

Die Konstante $\text{𝐜}$ gibt den Abstand zur x-Achse an. Die Parabel wird an der Geraden $\mathrm{y}=-1$ gespiegelt, also ist $c=-1$.

$\mathrm{y}=-\mathrm{0,5}{\mathrm{x}}^2+2$

Aufstellen der Funktionsgleichung der gespiegelten Parabel.

${\mathrm{y}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{p}}=2\mathrm{c}-(-\mathrm{0,5}{\mathrm{x}}^2+2)$

${\mathrm{y}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{p}}=2\cdot (-1)+\mathrm{0,5}{\mathrm{x}}^2-2$

${\mathrm{y}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{p}}=-2+\mathrm{0,5}{\mathrm{x}}^2-2$

$\underline{\underline{{\mathrm{y}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{p}}=\mathrm{0,5}{\mathrm{x}}^2-4}}$

Lösen der quadratischen Gleichung.

Lösen der quadratischen Gleichung mithilfe der Mitternachtsformel.

Die Mitternachtsformel lautet:

${\mathrm{x}}_{\mathrm{1,2}}={\displaystyle \frac{-\mathrm{b}\pm \sqrt{{\mathrm{b}}^2-4\mathrm{a}\mathrm{c}}}{2\mathrm{a}}}$

Lösungsmenge der quadratischen Gleichung: $𝕃=\{2;-3\}$

Aufgabenteil b.)

Berechnen des inneren Durchmessers der Wachskugel.

Die Formel zur Berechnung des Volumens einer Kugel lautet:

${\mathrm{V}}_{\text{Kugel}}={\displaystyle \frac{4}{3}}\cdot \mathrm{\pi }\cdot {\mathrm{r}}^3$

Auflösen der Formel nach $\text{r}$ :

$\mathrm{r}=\sqrt[3]{{\displaystyle \frac{3\cdot {\mathrm{V}}_{\mathrm{K}\mathrm{u}\mathrm{g}\mathrm{e}\mathrm{l}}}{4\cdot \mathrm{\pi }}}}$

Einsetzen des Volumens der Luft in die Formel.

$\mathrm{r}=\sqrt[3]{{\displaystyle \frac{3\cdot 998306}{4\cdot \mathrm{\pi }}}}$

$\mathrm{r}=\sqrt[3]{{\displaystyle \frac{2994918}{4\mathrm{\pi }}}}$

$\mathrm{r}=\sqrt[3]{\mathrm{238328,00}}$

$\mathrm{r}=62\text{ cm}$

Der innere Durchmesser der Wachskugel ist dann: $2\cdot 62\text{ cm}=124\text{ cm}$

Berechnen des Gewichtes des Bienenwachses in $\text{kg}$.

Berechnen des Volumens des Bienenwachses der Kugel.

${\mathrm{V}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}={\mathrm{V}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{t}}-{\mathrm{V}}_{\mathrm{L}\mathrm{u}\mathrm{f}\mathrm{t}}$

${\mathrm{V}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}={\displaystyle \frac{4\cdot \mathrm{\pi }\cdot {\mathrm{r}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{t}}^3}{3}}-{\mathrm{V}}_{\mathrm{L}\mathrm{u}\mathrm{f}\mathrm{t}}$

${\mathrm{r}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{t}}={\mathrm{r}}_{\mathrm{i}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{n}}+\mathrm{W}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{s}\mathrm{t}\ddot{\mathrm{a}}\mathrm{r}\mathrm{k}\mathrm{e}\Rightarrow {\mathrm{r}}_{\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{t}}=62+3=65$

${\mathrm{V}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}={\displaystyle \frac{4\cdot \mathrm{\pi }\cdot {65}^3}{3}}-998306$

${\mathrm{V}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}=\mathrm{1150346,51}-998306$

${\mathrm{V}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}=\mathrm{152040,51}{\text{ cm}}^3$

Das Bienenwachs der Kugel hat ein Volumen von:$\mathrm{152040,51}{\text{ cm}}^3$

Berechnen des Gewichtes des Bienenwachses.

${\mathrm{G}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}={\mathrm{V}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}\cdot \mathrm{0,9}$

${\mathrm{G}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}=\mathrm{152040,51}\cdot \mathrm{0,9}$

${\mathrm{G}}_{\mathrm{W}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{s}}=\mathrm{136836,46}\mathrm{g}$

Umrechnen des Gewichts des Wachses in $\text{kg}$.

${\displaystyle \frac{\mathrm{136836,46}}{1000}}=\mathrm{136,8}$

Das Gewicht des Bienenwachses beträgt: $\mathrm{136,8}\text{kg}$

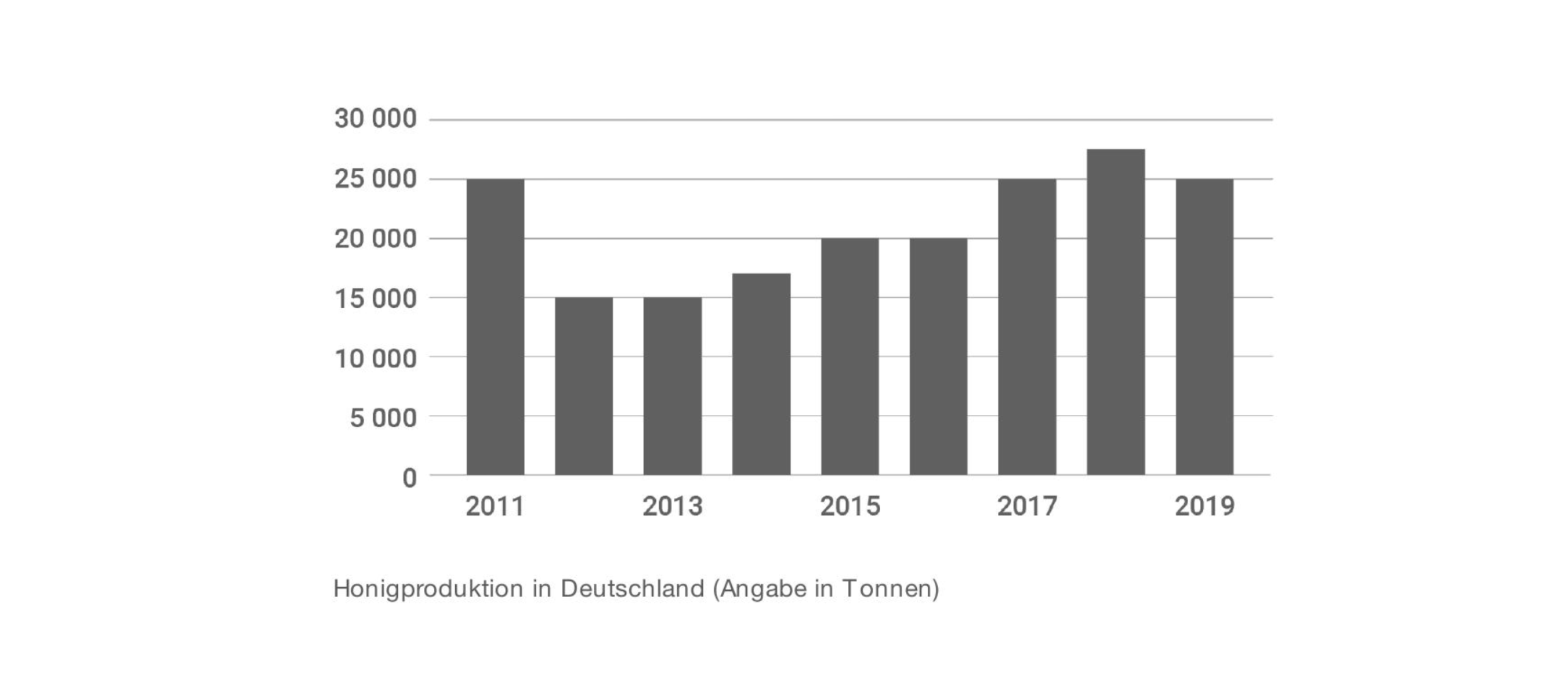
Berechnen der Menge an importiertem Honig in den Jahren 2012 und 2018.

Berechnen des gesamten Honigbedarfs im Jahr 2012.

${\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}\cdot {\displaystyle \frac{20}{100}}=15000\Rightarrow {\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}={\displaystyle \frac{15000\cdot 100}{20}}$

${\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}=75000\mathrm{t}$

Der gesamte Honigbedarf im Jahr 2012 betrug $75000\text{t}$.

Berechnen der Menge des importierten Honigs im Jahr 2012.

${\mathrm{G}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}.}={\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}-{\mathrm{G}}_{\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{P}.}$

${\mathrm{G}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}.}=75000-15000$

${\mathrm{G}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}.}=60000\mathrm{t}$

Im Jahr 2012 wurden $60000\mathrm{t}$ Honig importiert.

Berechnen des gesamten Honigbedarfs im Jahr 2018.

${\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}\cdot {\displaystyle \frac{20}{100}}=27500\Rightarrow {\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}={\displaystyle \frac{27500\cdot 100}{20}}$

${\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}=137500\mathrm{t}$

Der gesamte Honigbedarf im Jahr 2018 betrug $137500\text{t}$.

Berechnen der Menge des importierten Honigs im Jahr 2018.

${\mathrm{G}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}.}={\mathrm{G}}_{\mathrm{g}\mathrm{e}\mathrm{s}}-{\mathrm{G}}_{\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{P}.}$

${\mathrm{G}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}.}=137500-27500$

${\mathrm{G}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}.}=110000\mathrm{t}$

Im Jahr 2018 wurden $110000\mathrm{t}$ Honig importiert.