Der Flächeninhalt von Dreiecken kann durch die Vervollständigung auf ein Rechteck berechnet werden.
Aus dieser Vervollständigung gehen die Formeln zur Flächenberechnung hervor:
Der Flächeninhalt des rechtwinkligen Dreiecks
Der Flächeninhalt eines Dreiecks gibt an, wie groß die Fläche innerhalb der Linien des Dreiecks ist.
Um den Flächeninhalt eines rechtwinkligen Dreiecks zu berechnen, verwendet man eine Erweiterung zum Rechteck.
Man kann dann nämlich sehen, dass das Dreieck genau die Hälfte des Rechtecks ausmacht, denn die Diagonale halbiert das Rechteck. Den Flächeninhalt des Rechtecks kann man nach Formel berechnen mit:
Dabei sind und die Grundlinie und die Höhe des Dreiecks.
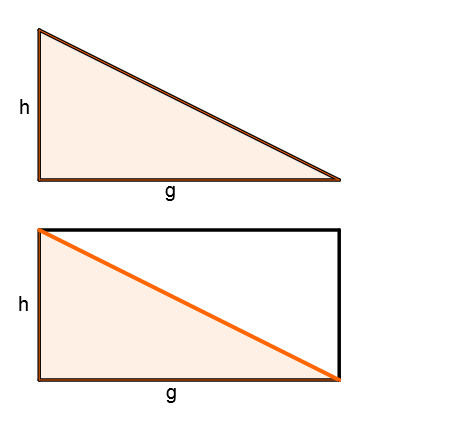
Man erhält also, dass
des Rechtecks, doppelt so viel Flächeninhalt ergibt, wie das rechtwinklige Dreieck hat.
Somit kommt man auf die Formel für den Flächeninhalt des rechtwinkligen Dreiecks:
Der Flächeninhalt von allgemeinen Dreiecken
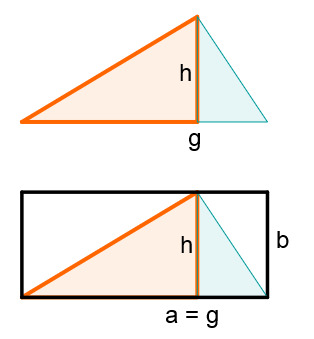
Um den Flächeninhalt von Dreiecken ohne besondere Eigenschaften zu berechnen, greifen wir auf die Berechnung von Flächeninhalten von rechtwinkligen Dreiecken zurück.
Man sieht in der oberen Abbildung, dass die Höhe das Dreieck in zwei kleinere Teildreiecke teilt.
Beide Teildreiecke sind rechtwinklige Dreiecke, denn die Höhe steht immer im rechten Winkel zur Grundlinie (hier g).
Damit hat man jetzt das Dreieck in zwei kleinere Dreiecke aufgeteilt, deren Flächeninhalt man wie oben berechnen kann.
Die Vervollständigung beider kleinen Dreiecke zu einem Rechteck zeigt (rechts im Bild), dass die Seitenlänge des Rechtecks die ganze Grundseite beträgt.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
