8. Abbildungen

Eine Abbildung oder Funktion $f : A \to B$ ist eine Relation, bei der es für jedes $a \in A$ genau ein $b \in B$ gibt, das mit $a$ in Relation steht. Wir schreiben dann $a \mapsto b$ oder $b = f (a)$ .

Beispiel

Du kannst z.B. aus der Tier-Relation aus Kapitel 6 durch Entfernen von Paaren (bzw. Pfeilen) eine Abbildung machen:

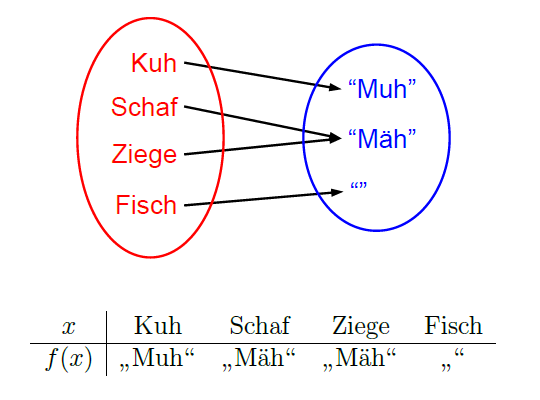
Diese Tabelle ist die Wertetabelle der Abbildung.

Definitionsbereich und Wertevorrat

Für eine Funktion $f : A \to B$ heißt $A$ der Definitionsbereich und $B$ der Wertevorrat von $f$ . Beide gehören zur Funktion!

Daher sind $f (x) = x$ mit $A = [0,1], B = ℝ$ und $f (x) = x$ mit $A = B = [0,1]$ zwei verschiedene Abbildungen!

Bildmenge und Urbildmenge

Der Wertevorrat muss nicht ausgeschöpft werden. Die Menge der Elemente des Wertevorrats $B$ , die tatsächlich als Bildelemente auftreten, heißt die Bildmenge (auch: das Bild) von $A$ (unter $f$ ):

$f (A) = {f (x) | x \in A}$

Zu einem $b \in B$ ist

$f^{- 1} (b) = {a \in A | f (a) = b}$

die Urbildmenge (auch: das Urbild) von $b$ . Vorsicht: $b$ ist ein einzelnes Element, aber $f^{- 1} (b) \subseteq A$ ist eine Menge mit eventuell mehreren oder keinen Elementen.

Injektivität, Surjektivität und Bijektivität

Es folgen drei Begriffe, die zum Glück nicht so kompliziert sind, wie sie klingen.

Eine Abbildung $f : A \to B$ heißt

injektiv, wenn gilt:

\forall b \in B : | f^{- 1} (b) | \leq 1,

d.h. jedes $b$ aus dem Wertevorrat hat höchstens ein Urbild.

surjektiv, wenn gilt:

\forall b \in B : | f^{- 1} (b) | \geq 1,

d.h. jedes $b$ aus dem Wertevorrat hat mindestens ein Urbild.

bijektiv, wenn gilt:

\forall b \in B : | f^{- 1} (b) | = 1,

d.h. jedes $b$ aus dem Wertevorrat hat genau ein Urbild.

Bijektiv bedeutet also injektiv und surjektiv. Bei einer bijektiven Abbildung $f$ ist die Umkehrung $f^{- 1}$ ebenfalls eine Abbildung.

Der deutsche Begriff für injektiv lautet eineindeutig - die Abbildung $f$ ist eindeutig, und die Umkehrung $f^{- 1}$ ist auch eindeutig. Der deutsche Begriff für surjektiv lautet auf - die Elemente des Definitionsbereichs $A$ werden auf den Wertevorrat $B$ abgebildet und nicht nur in den Wertevorrat. Und der deutsche Begriff für bijektiv lautet umkehrbar eindeutig.

Beispiele

Die Funktion $f : ℝ \to ℝ, f (x) = x^{2}$ ist nicht injektiv. Denn beispielsweise werden sowohl $2$ als auch $- 2$ werden auf $4$ abgebildet. Die $4$ hat also die Urbildmenge ${- 2, 2}$ .
Die Funktion ist auch nicht surjektiv, denn die negativen Zahlen treten nicht als Bildelemente auf.
Wenn du den Definitionsbereich und den Wertevorrat auf die positiven reellen Zahlen $ℝ^{+}$ einschränkst, erhältst du eine injektive und surjektive, also bijektive Abbildung $f : ℝ^{+} \to ℝ^{+}$ .

Abzählbarkeit

Eine Menge $M$ ist abzählbar genau dann, wenn es eine bijektive Abbildung zwischen $M$ und $ℕ$ gibt. Dadurch ergibt sich quasi ein Nummerierung der Elemente von $M$ .

Beispiel

Die Menge der ganzen Zahlen $ℤ$ ist abzählbar. Eine bijektive Abbildung $f : ℤ \to ℕ$ ist gegeben durch

f (z) = {\begin{aligned} 2 z & falls z \geq 0 \\ - 2 z - 1 & sonst \end{aligned}

Die Zahlen $0, 1, 2, . . .$ werden also auf die geraden Zahlen $0,2,4, . . .$ abgebildet, die negativen Zahlen $- 1, - 2, - 3, . . .$ werden auf die ungeraden Zahlen $1, 3, 5, . . .$ abgebildet.

Die Menge $ℚ$ der rationalen Zahlen ist abzählbar. Die Menge der reellen Zahlen $ℝ$ ist dagegen nicht abzählbar. Du beweist diese beiden Tatsachen mit dem ersten bzw. mit dem zweiten cantorschen Diagonalverfahren.

Laden

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?