Bei der Spiegelung an einer Ursprungsgeraden wird ein Punkt an einer Gerade gespiegelt, die das Winkelmaß besitzt und durch den Ursprung verläuft.
Abbildungsgleichung der Spiegelung an einer Ursprungsgerade
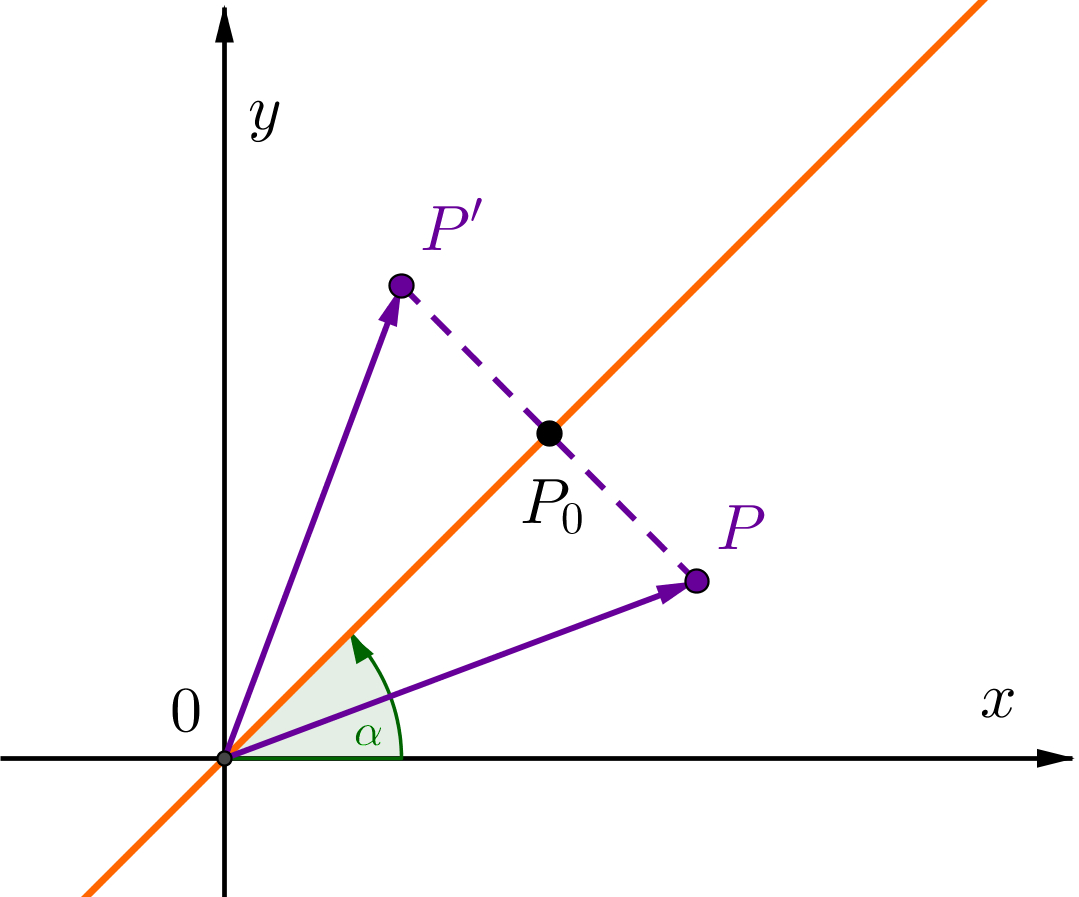
Koordinatenform:
Matrixform:
Beispiel:
Spiegle den Punkt an der Ursprungsgerade .
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
