Verknüpfung von Abbildungen

Die verschiedenen Abbildungen im Koordinatensystem können ohne Problem hintereinander ausgeführt werden.

Häufige Verknüpfungen

Jegliche Abbildungen in der Ebene können miteinander verknüpft werden. In diesem Artikel werden nur die häufigsten behandelt.

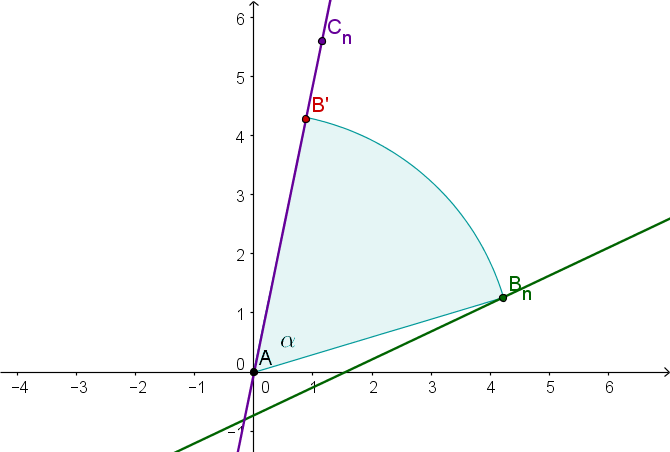
Drehung und zentrische Streckung

Hierbei wird der Punkt $B_{n}$ zuerst um den Winkel $α$ um den Punkt $A$ auf $B^{'}$ gedreht und dann um den Faktor $k$ auf den Punkt $C_{n}$ zentrisch gestreckt. Rechnerisch erreicht man dies, indem man zuerst die Drehung und dann die Streckung ausführt.

$(\begin{array}{c} x_{B^{'}} \\ y_{B^{'}} \end{array}) = (\begin{array}{cc} \cos α & - \sin α \\ \sin α & \cos α \end{array}) \cdot (\begin{array}{c} x_{B_{n}} \\ y_{B_{n}} \end{array})$

$(\begin{array}{c} x_{C_{n}} \\ y_{C_{n}} \end{array}) = (\begin{array}{cc} k & 0 \\ 0 & k \end{array}) \cdot (\begin{array}{c} x_{B^{'}} \\ y_{B^{'}} \end{array})$

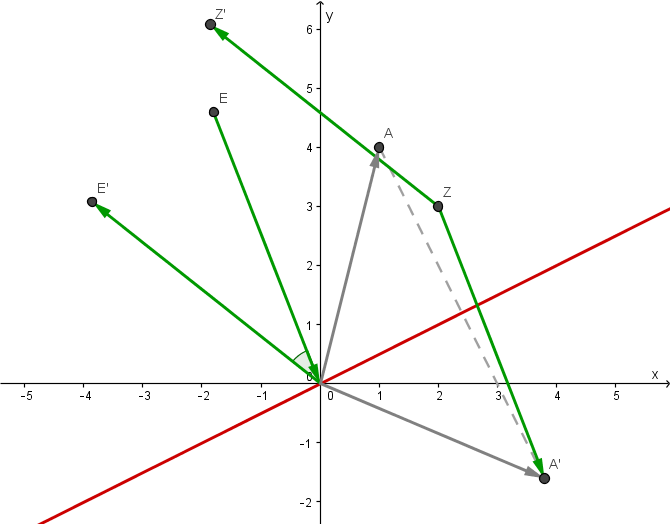
Spiegelung an einer Ursprungegeraden und Drehung

Hierbei wird der Punkt $A$ an der roten Ursprungsgeraden gespiegelt und anschließend um den grünen Winkel um das Zentrum $Z$ auf $Z^{'}$ gedreht.

$(\begin{array}{c} x_{A^{'}} \\ y_{A^{'}} \end{array}) = (\begin{array}{cc} \cos 2 α & \sin 2 α \\ \sin 2 α & - \cos 2 α \end{array}) \cdot (\begin{array}{c} x_{A} \\ y_{A} \end{array})$

$(\begin{array}{c} x_{Z^{'}} \\ y_{Z^{'}} \end{array}) = (\begin{array}{rcl} \cos α - \sin α \\ \sin α \cos α \end{array}) \cdot \vec{Z A^{'}} + \vec{O Z}$

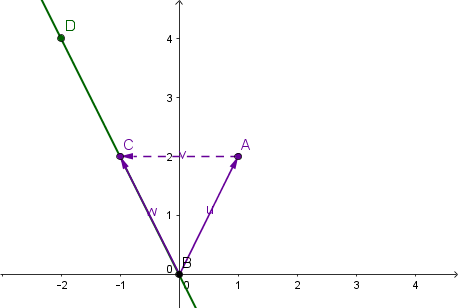
Parallelverschiebung und zentrische Streckung

Hierbei wird zuerst $A$ um den Vektor $v$ auf $C$ parallel verschoben und dann um den Faktor $k$ auf $D$ gestreckt.

$(\begin{array}{c} x_{C} \\ y_{C} \end{array}) = (\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}) \cdot (\begin{array}{c} x_{A} \\ y_{A} \end{array}) + (\begin{array}{c} v_{x} \\ v_{y} \end{array})$

$(\begin{array}{c} x_{D} \\ y_{D} \end{array}) = (\begin{array}{cc} k & 0 \\ 0 & k \end{array}) \cdot (\begin{array}{c} x_{C} \\ y_{C} \end{array})$

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?