Aufgaben zur Zinsrechnung - lernen mit Serlo!

Zwei Banken liefern sich einen Wettbewerb um die Gunst der Kunden.

Bank A sagt: "Bei uns bekommen Sie 8% Zins auf ihre Spareinlagen."

Bank B sagt: "Bei uns bekommen Sie zweimal im Jahr, nämlich einmal Ende

Juni und einmal Ende Dezember, 4% Zins auf Ihrem Konto gutgeschrieben."

Begründe rechnerisch, bei welcher Bank man als Kunde besser fährt.

Bank A ist das bessere Angebot.
Bank B ist das bessere Angebot.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zinsrechnung

Gegeben: Bank A: 8% Zinsen pro Jahr Bank B: 4% Zinsen pro halbes Jahr

Gefragt:

Bei welcher Bank wäre am Ende des Jahres mehr Geld auf dem Konto?

Bei Bank A gib es pro Jahr 8% Zinsen. Nach einem Jahr sind also 108% des Startkapitals auf dem Konto.

Bei Bank B hingegen gibt es 4% Zinsen im ersten halben Jahr. Nach einem halben Jahr sind 104% des Startkapitals auf dem Konto. Auf diese 104% gibt es im zweiten halben Jahr erneut 4%. Nach einem weiteren halben Jahr sind 104% des Zwischenkapitals auf dem Konto.

Nach einem Jahr steigt das Kapital somit um: $1,04 \cdot 1,04 = 1,0816$

Am Ende des Jahres sind also 108,16% des Startkapitals auf dem Konto.

$\Rightarrow$ Bei Bank B kommen im ersten Jahr 8,16% des Startkapitals dazu. Bei Bank A nur 8%.

$\Rightarrow$ Bank B ist also besser als Bank A.

Alternative Begründung anhand eines Beispiels

Gehe von einem Kapital von $1 000$ Euro aus.

Gegeben: Bank A: 8% Zinsen pro Jahr; Bank B: 4% Zinsen pro halbes Jahr

Gesucht: Kapital nach einem Jahr

Bank A:

Berechne die Zinsen bei Bank A nach einem Jahr mit der Formel.

$Z = p \cdot K$ $= 8 % \cdot 1 000 €$ $= 0,8 \cdot 1 000 €$ $= 80 €$

Der Zinsbetrag wird zur Anlage addiert.

$K^{+} = 1000 € + 80 € = 1080 €$

Also hast du nach einem Jahr $1080 €$ auf dem Konto.

Bank B:

Berechne das neue Kapital bei Bank B nach einem halben Jahr mit der Formel.

$Z = p \cdot K$ $= 4 % \cdot 1 000 €$ $= 0,4 \cdot 1 000 €$ $= 40 €$

Der Zinsbetrag wird zur Anlage addiert.

$K^{+} = (1 000 € + 40 €)$ $= 1 040 €$

Berechne die Zinsauszahlung am Ende des zweiten halben Jahres. Beachte, dass sich die 4% Zinsen nun auf den vermehrten Grundwert $K^{+}$ beziehen.

$Z = p \cdot K^{+}$ $= 4 % \cdot 1 040 €$ $= 0,4 \cdot 1 040 €$ $= 41,60 €$

Berechne die Summe an Zinsen bei Bank B.

$40 € + 41,60 € = 81,60 €$

Also hast du nach einem Jahr

$1000 € + 81,60 € = 1081,60 €$ auf dem Konto.

Vergleiche jeweils die Zinsbeträge, die du nach einem Jahr bekommen hast.

Ergebnis

Während du bei Bank A lediglich $80 €$ erhältst, sind es bei Bank $81,6 €$ . Also fährst du als Kunde bei Bank B besser.

Alternative Begründung anhand eines Beispiels mit Dreisatz

Gehe von einem Kapital von $1 000$ Euro aus.

Gegeben: Bank A: 8% Zinsen pro Jahr Bank B: 4% Zinsen pro halbes Jahr

Gesucht: Kapital nach einem Jahr

Bank A:

Berechne die Zinsen bei Bank A nach einem Jahr mit dem Dreisatz.

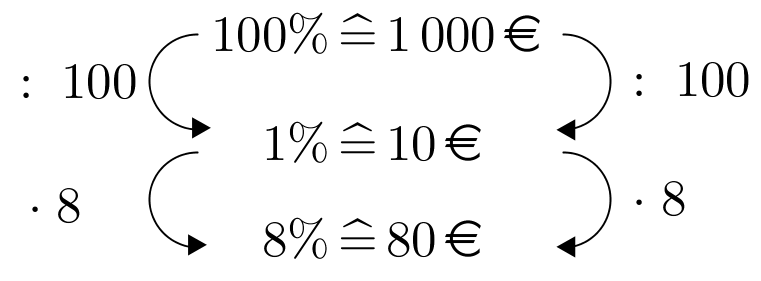
Also hast du nach einem Jahr

$1000 € + 80 € = 1080 €$ auf dem Konto.

Der Zinsbetrag wird zur Anlage addiert.

Bank B:

Berechne das neue Kapital bei Bank B nach einem halben Jahr.

Der Zinsbetrag wird zur Anlage addiert.

$K^{+} = (1 000 € + 40 €)$ $K^{+} = 1 040 €$

Berechne die Zinsauszahlung am Ende des zweiten halben Jahres. Beachte, dass sich die 4% Zinsen nun auf den vermehrten Grundwert $K^{+}$ beziehen.

Berechne die Summe an Zinsen bei Bank B.

$40 € + 41,60 € = 81,60 €$

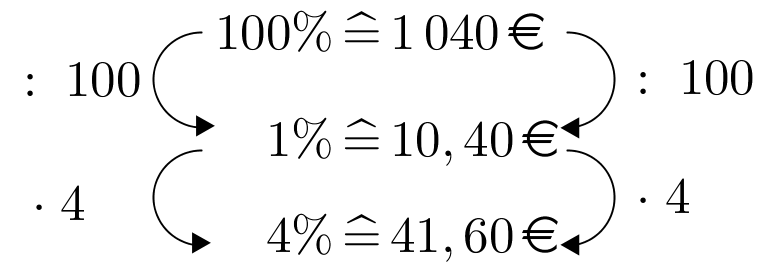
Also hast du nach einem Jahr

$1000 € + 81,60 € = 1081,60 €$ auf dem Konto.

Vergleiche jeweils die Zinsbeträge, die du nach einem Jahr bekommen hast.

Ergebnis

Während du bei Bank A lediglich $80 €$ erhältst, sind es bei Bank $81,6 €$ . Also fährst du als Kunde bei Bank B besser.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?