1 Symmetrie (1|3)
Achsensymmetrie zur y-Achse
Jede ganzrationale Funktion, bei der die Variable
nur in Potenzen mit geradem Exponenten vorkommt,
ist achsensymmetrisch zur y-Achse.

Beispiel für einen Graphen, der achsensymmetrisch zur y-Achse ist.
2 Symmetrie (2|3)
Punktsymmetrie zum Ursprung
Jede ganzrationale Funktion, bei der die Variable
nur in Potenzen mit ungeradem Exponenten vorkommt,
ist punktsymmetrisch zum Ursprung (0|0).
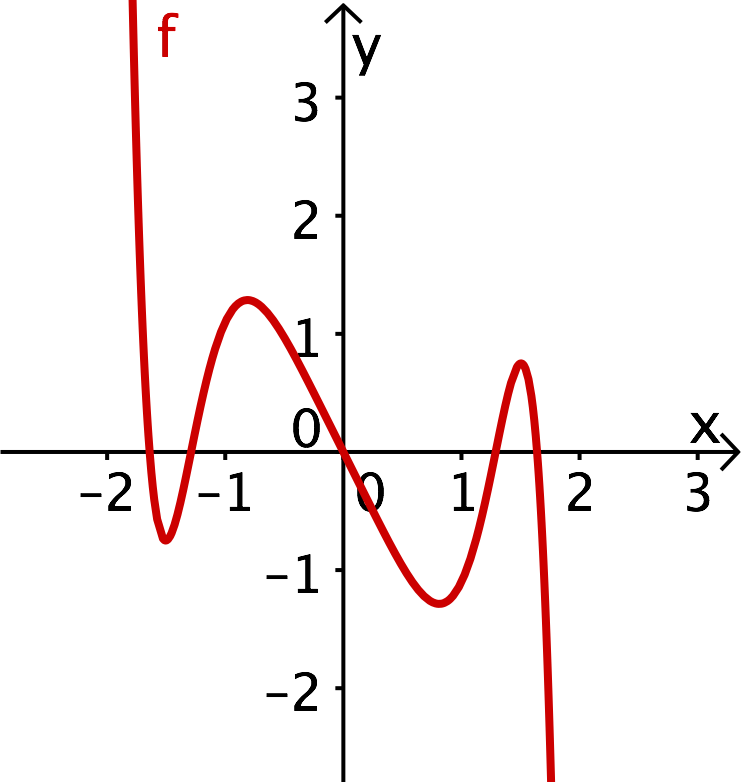
Beispiel für einen Graphen, der punktsymmetrisch zum Ursprung ist
3 Symmetrie (3|3)
Keine Symmetrie zum Koordinatensystem
Wenn in einer ganzrationalen Funktion die Variable
als Potenz mit geradem Exponenten
und außerdem auch
als Potenz mit ungeradem Exponenten vorkommt,
ist der Graph weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
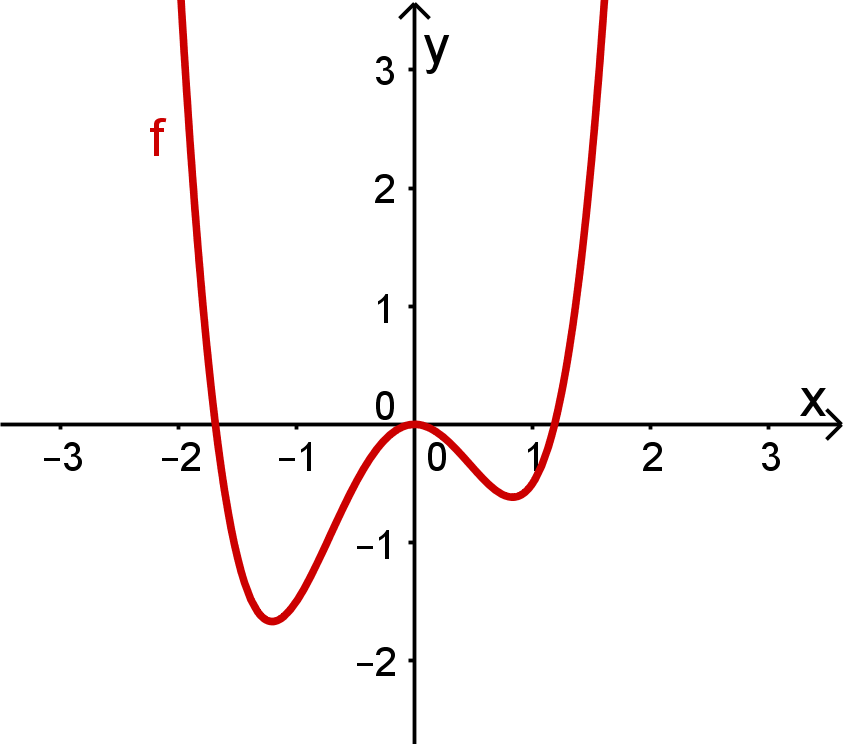
Beispiel für einen Graphen, der keine Symmetrie zum Koordinatensystem aufweist
Ob es Achsensymmetrie zu einer anderen Achse als der y-Achse oder Punktsymmetrie zu einem anderen Punkt als dem Ursprung gibt, ist eine andere Frage, die schwieriger zu beantworten ist und hier nicht behandelt werden soll.
4 Erster Schritt: Nullstellen bestimmen (3)
Wie das Ausrechnen der Nullstellen aus der Gleichung geht, hängt natürlich immer von der Art der Funktion ab.

Gibt es denn da gar keine allgemeine Regel, die immer funktioniert?
Eine allgemeine Regel, die immer in der gleichen Weise funktioniert, gibt es da nicht.
Aber ein paar Tipps - oder eine Art "Anleitung", die (fast) immer funktioniert - kann ich dir für solche Polynomfunktionen, wie unser es ist, schon geben:
Falls in der Gleichung überhaupt kein usw. vorkommt, dann
stellst du die Gleichung einfach nach um.
Wenn die höchste vorkommende x-Potenz ist, kannst du
die Lösungsformel der quadratischen Gleichung anwenden.
Wenn auch höhere Potenzen von vorkommen,
schaust du zunächst, ob du ausklammern kannst
- und wenn das geht, dann tust du es natürlich.
5 Beispiel - Nullstellenbestimmung (1| )

Nun gut, in unserem Beispiel müssen wir zunächst einmal die Nullstellen bestimmen.
Die Funktion ist
Dann fangen wir mit der Arbeit an…

…und jeder von uns Dreien -
denn du da draußen vor dem Bildschirm, du machst doch mit, oder? -
versucht es zunächst einmal alleine…

…und wenn wir nicht weiterkommen, treffen wir uns alle auf der nächsten Kursseite!
6 Nullstellen im Beispiel (2| )

Die Funktion gleich 0 setzen ist ja nicht schwer:
Aber wie geht es weiter?
Bei solchen Polynomgleichungen sollte man immer zunächst prüfen,
ob man oder sogar usw. ausklammern kann.


In unserer Gleichung kann man ausklammern!
Also so:
7 Nullstellen im Beispiel (4|4)
Weil das ein Produkt ist, und weil ein Produkt genau dann 0 wird, wenn einer der Faktoren 0 ist,
kann man hier beide Faktoren einzeln gleich 0 setzen.

Der Faktor ergibt die Nullstelle .
Und dann setzen wir einfach noch den Term in der Klammer gleich 0:

?
Darauf kann man doch
die Lösungsformel der quadratischen Gleichung anwenden:
*Das mach' ich doch gleich mal!
Wir sehen uns dann auf der nächsten Kursseite!*
