Problematische Prozentangaben

1 Einleitung

Dieser Kurs beschäftigt sich mit Prozentangaben, welche im Alltag oft vorkommen, allerdings meistens nicht richtig verstanden werden.

2 Prozentangaben bei Steigungen

Wenn du mit dem Fahrrad unterwegs warst, ist dir bestimmt schon öfter ein Schild aufgefallen, welches die Steigung eines Berges in Prozent angibt.

Bei dem hier gezeigten Schild wird eine Steigung von $12 %$ angezeigt.

Nimm dir nun einen Zettel und überlege dir, wie steil wohl der Berg sein wird. Vielleicht hast du auch schon eine Idee, wie viel Grad das wohl in der Wirklichkeit entspricht?

3 Prozentangaben bei Steigungen

Überlegt man sich nun, was die Prozentangabe auf dem Verkehrsschild für einer Gradzahl entsprechen könnte, muss man sich erst einmal überlegen, wie die Prozentangabe hier entsteht.

Prozent steht immer für einen Anteil von etwas Ganzem. So entsprechen $10 %$ von 200 Leuten 20 Leuten, da $\displaystyle 10\,\% = \frac{10}{100} = \frac{1}{10}$ und ein Zehntel von 200 gleich 20 ist.

Möchte man nun also eine Steigung berechnen, berechnet man den Anteil der zurückgelegten Höhe an der zurückgelegten Länge der Strecke im Waagrechten. Also zurückgelegt senkrecht $:$ zurückgelegt waagrecht = $12 %$ .

Nun kannst du dir eine Skizze auf einem Blatt Papier machen:

Zeichne dort $10\,\mathrm{cm}$ waagrecht nach rechts und anschließend $1{,}2\,\mathrm{cm}$ senkrecht nach oben.

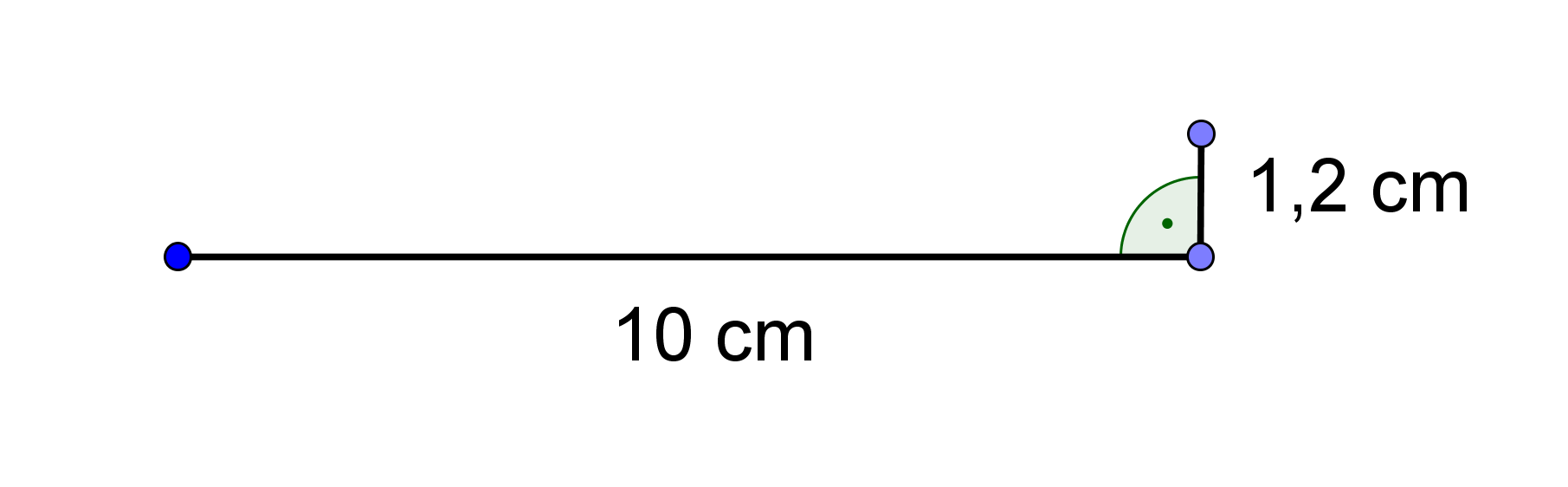
Verbindest du nun das Ganze zu einem Dreieck, kannst du den Winkel der Steigung messen.

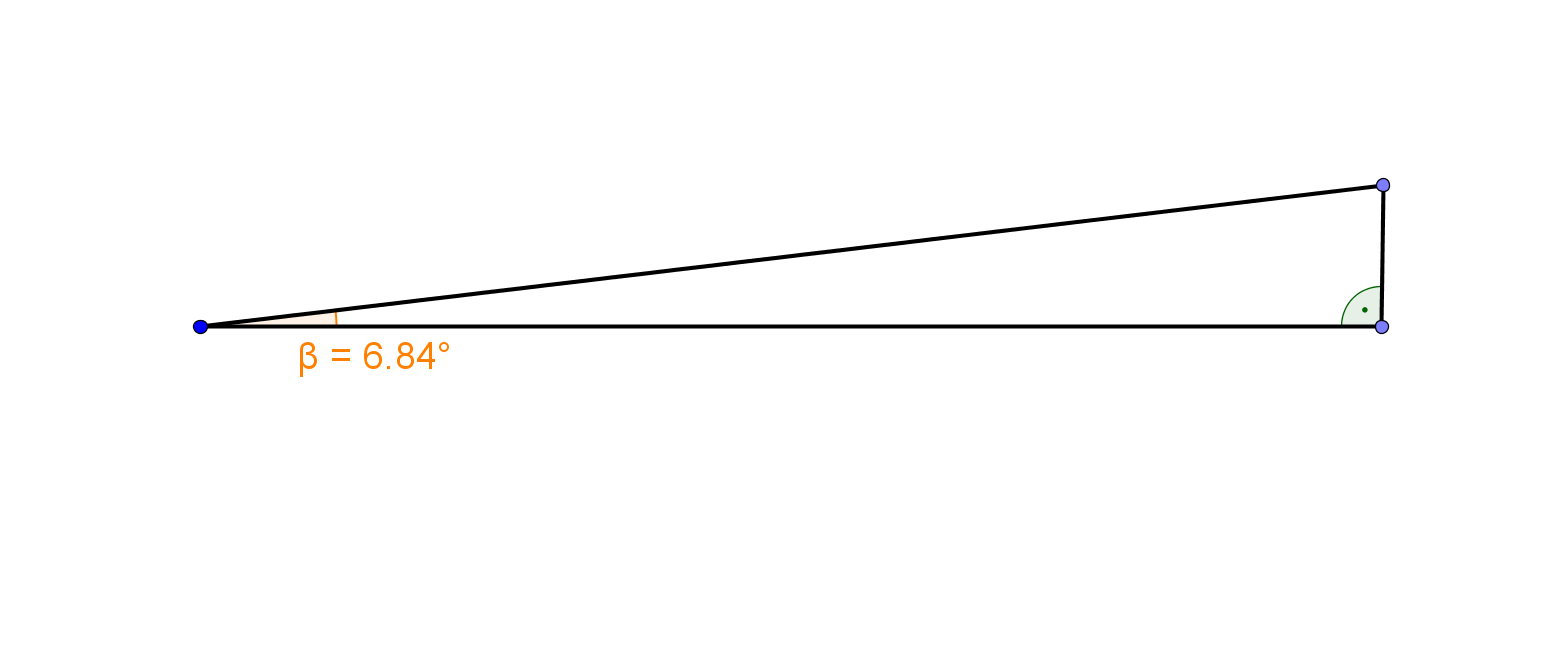
Hier entspricht der Winkel etwa $6,84 °$ .

Wie gut warst du mit deiner Schätzung?

4 Prozentangaben bei Steigungen

Einmal im Jahr findet das berühmte Skirennen an der Streif in Kitzbühl statt. Die Strecke gilt als besonders heimtückisch und das nicht nur wegen der über $140\,\mathrm{km/h}$ Spitzengeschwindigkeit, sondern auch wegen der steilsten Stelle der Strecke, der sogenannten Mausfalle.

Sie heißt so, weil die Skifahrer mit sehr hoher Geschwindigkeit auf ein Gefälle von $85 %$ zufahren und quasi blind hereinspringen.

Versuche doch nun, herauszufinden, wie viel Grad dieses Gefälle entspricht!

5 Prozentangaben bei Steigungen

Wie auf den vorherigen Seiten thematisiert, bedeuten $85\,\mathrm{\%}$ Steigung, dass die senkrecht zurückgelegte Strecke $85\,\mathrm{\%}$ von der waagrecht zurückgelegten Strecke ausmacht.

Mache dir nun also wieder eine Skizze:

In der Waagerechten trägst du $10\,\mathrm{cm}$ an und in der Senkrechten $8{,}5\,\mathrm{cm}$ .

Verbinde nun noch die beiden Enden zu einem Dreieck.

Nun kannst du den Winkel messen!

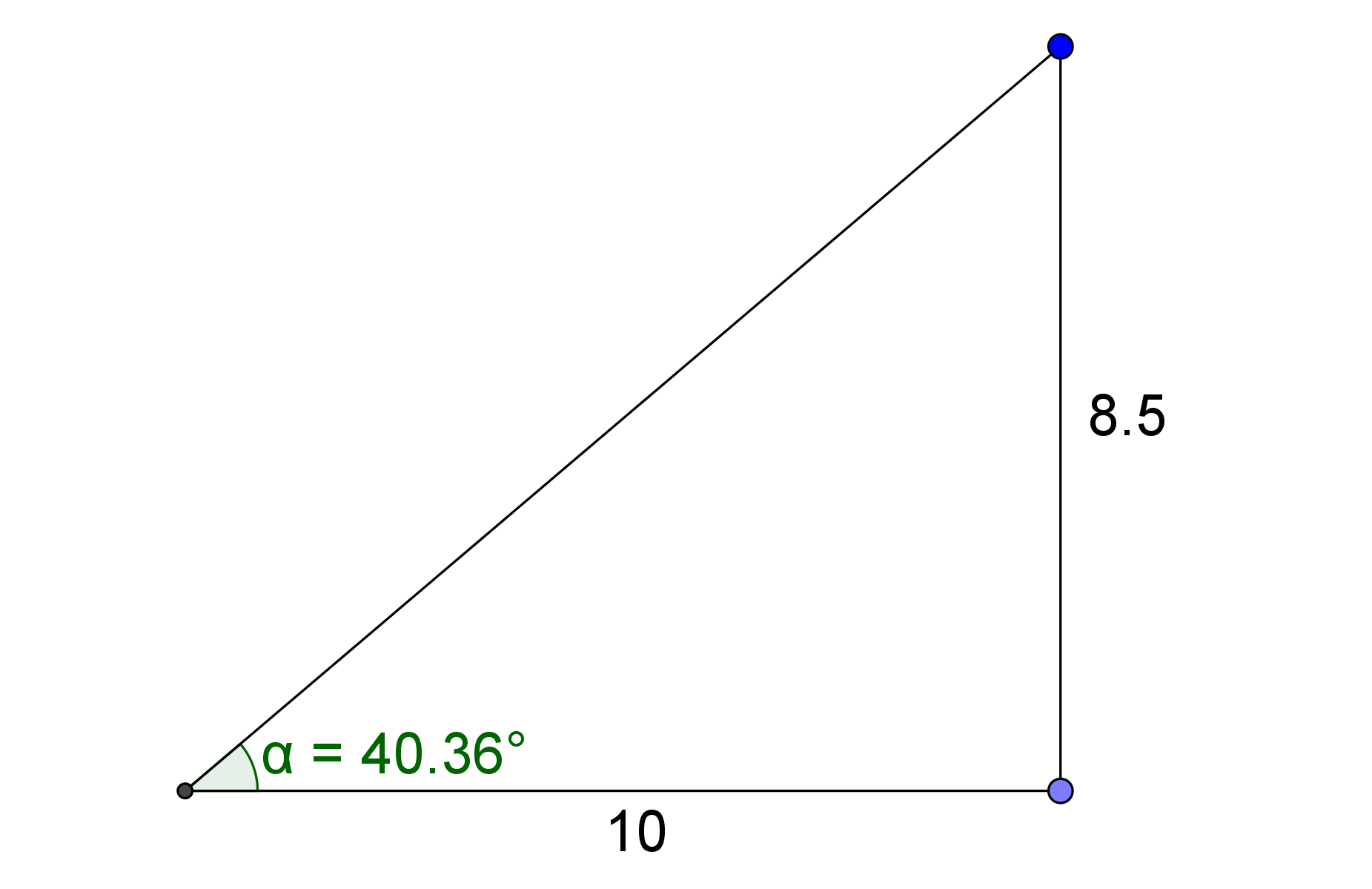
Überrascht dich das Ergebnis? Viele haben vermutlich deutlich mehr Grad vermutet!

Ein kleiner Tipp für die Zukunft:

Eine Steigung von $100\,\mathrm{\%}$ entspricht $45 °$ !

6 Problematische Prozentangaben bei Diagrammen

Nun sind alle Fußballexperten gefragt, aber auch alle, die nicht so viel Ahnung von Fußball haben, können leicht mitraten!

Die beiden Diagramme unten zeigen jeweils die Anzahl der Siege einer Fußballmannschaft. Überlege dir jeweils, um welche Mannschaft es sich handeln könnte!

Schreibe dir alle deine Gedanken in Stichpunkten auf einen Zettel.

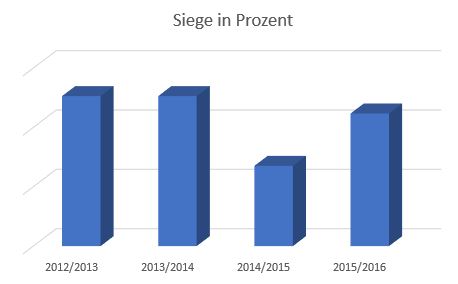
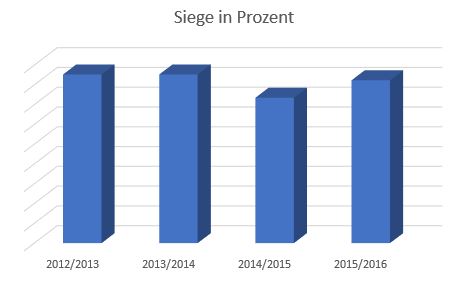
7 Problematische Prozentangaben bei Diagrammen

Die Lösung der Frage überrascht dich wahrscheinlich.

Beide Diagramme gehören zu demselben Diagramm!

Und zwar zum FC Bayern München.

Wie kann das sein? Schauen wir uns das Ganze auf der nächsten Kursseite gemeinsam einmal an!

8 Problematische Prozentangaben bei Diagrammen

Die Lösung wird dir recht einfach vorkommen!

Wenn du dir die beiden Diagramme noch einmal anschaust, siehst du, dass die senkrechte Beschriftung der $y$ -Achse fehlt.

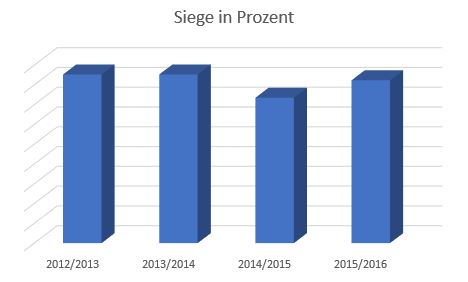
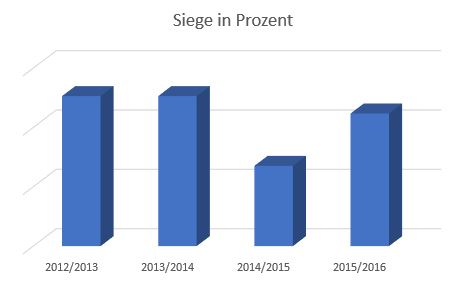
Ergänzt man die $y$ -Achse, fällt Folgendes auf:

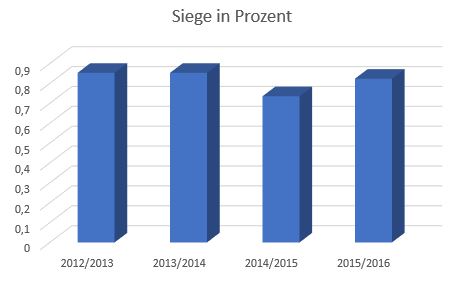
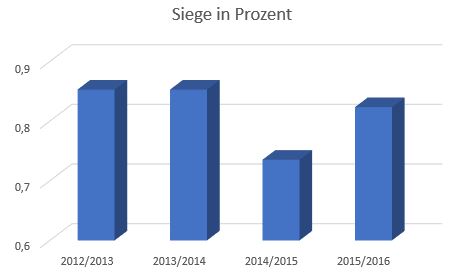
Durch die nun hinzugefügte Beschriftung der $y$ -Achse sieht man, dass bei dem rechten Diagramm ein wenig getrickst wurde, damit die Unterschiede größer aussehen!

Achte also auch im Alltag darauf, welchem Diagramm du glauben kannst.

Merke: Fehlen bei einem Diagramm die Achsenbeschriftungen, sei besonders vorsichtig und überlege, ob das Diagramm stimmen kann!