Aufgaben zum Anwenden der Rechengesetze
Überprüfe dein Wissen zum Kommutativ-, Assoziativ- und Distributivgesetz mit diesen gemischten Aufgaben!
- 1
Berechne den Term möglichst geschickt:
- 2
Berechne das Produkt möglichst geschickt:
- 3
Das Distributivgesetz beschreibt eine Aufteilung, die mit einer tatsächlichen Handlung in Verbindung gebracht werden kann.
Überlege dir eine Geschichte, die den Term in einer Handlung beschreibt.
- 4
Ein Punktemuster stellt die Aufteilung sehr schön dar, die das Distributivgesetz beschreibt. In den folgenden Aufgaben kannst du ein Punktemuster skizzieren, welches die in der Geschichte beschriebe Aufteilung veranschaulicht. Umgekehrt kannst du auch eine Geschichte verfassen, welche die Aufteilung des Punktemusters in einer Handlung beschreibt.
Lies die folgende Geschichte.
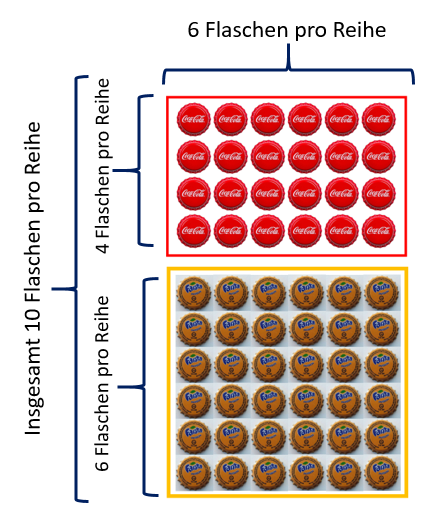
Paula und Lisa kaufen für eine Party zwei Getränkekisten. In einer Kiste sind 4x6 Flaschen Cola, in der anderen Kiste sind 6x6 Flaschen Fanta.
Wie viele Flaschen haben die beiden insgesamt gekauft? Veranschauliche die Frage in einem Bild.
Schreibe jetzt selber eine Geschichte zu der Aufteilung im Bild.

- 5
Peter und Lisa möchten zusammen einen Tagesausflug machen und gehen dafür 3 Mal arbeiten, um das Geld dafür anzusparen. Der Arbeitgeber gibt Peter für jeden Tag 8 Euro und Lisa 10 Euro.
Lisa freut sich, dass sie ein bisschen mehr verdient als Peter. Daher rechnet sie am Ende ihr gesamtes Gehalt und Peters gesamtes Gehalt zusammen und addiert beides erst zum Schluss.
Peter rechnet erst ihre Tagesgehälter zusammen und schaut daraufhin, wie viel sie in drei Tagen verdienen.
Schreibe beide Rechenwege auf. Kommen sie auf das gleiche Ergebnis?
- 6
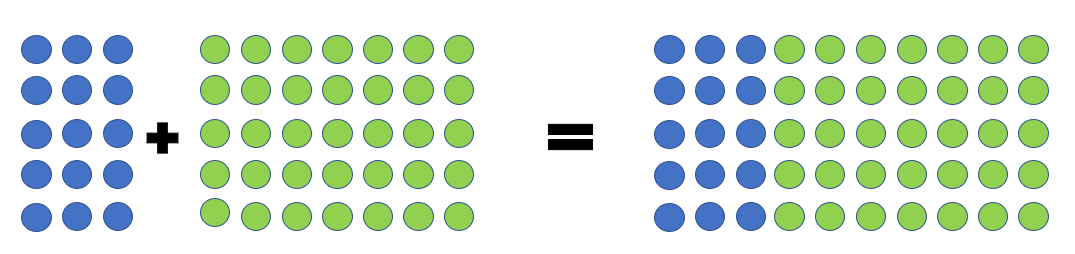
Stelle beide Seiten des Terms auf, welcher die Aufteilung des Punktemusters mathematisch beschreibt.
- 7
Punktemuster beschreiben eine Aufteilung, welche durch einen mathematischen Term beschrieben wird. Ordne den Termen das richtige Punktemuster zu.
Welches Bild passt zu der Formel
?
Bild 1

Bild 2

Bild 3

Bild 4

Welches Bild passt zum Term ?
Bild 1

Bild 2

Bild 3

Bild 4

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?