Das Distributivgesetz oder "Verteilungsgesetz" erlaubt das Aus-multiplizieren bzw. Ausklammern von Termen.
Bei der Multiplikation einer Summe/Differenz mit einem Faktor werden die Summanden beispielsweise nacheinander mit demselben Faktor multipliziert:
bzw.
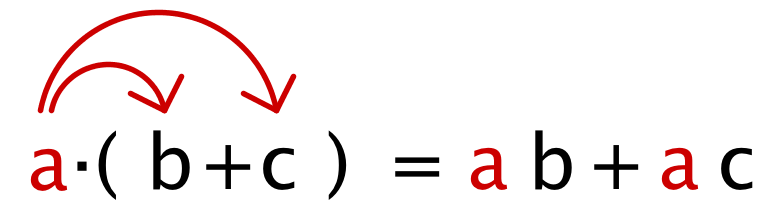
Erklärung des Gesetzes am Beispiel
Stelle dir vor, du schuldest deinen fünf Freunden jeweils 12 Euro und möchtest ihnen das Geld zurückgeben. Leider hast du heute deine Münzen zu Hause vergessen. Nun hast du zwei Möglichkeiten, ihnen das Geld zurückzugeben:
Entweder du gibst heute allen 5 Freunden 10 Euro und reichst morgen jeweils die fehlenden 2 Euro nach.
Alternativ kannst du aber auch morgen das ganze Geld mitnehmen und allen auf einmal jeweils 12 Euro zurückgeben.
Diese Handlung kann mithilfe eines mathematischen Terms beschrieben werden:
Beide Terme beschrieben den gleichen Wert, womit gelten muss:
Die Bedeutung dieser Rechnung kann man anhand eines Punktemusters besser nachvollziehen:
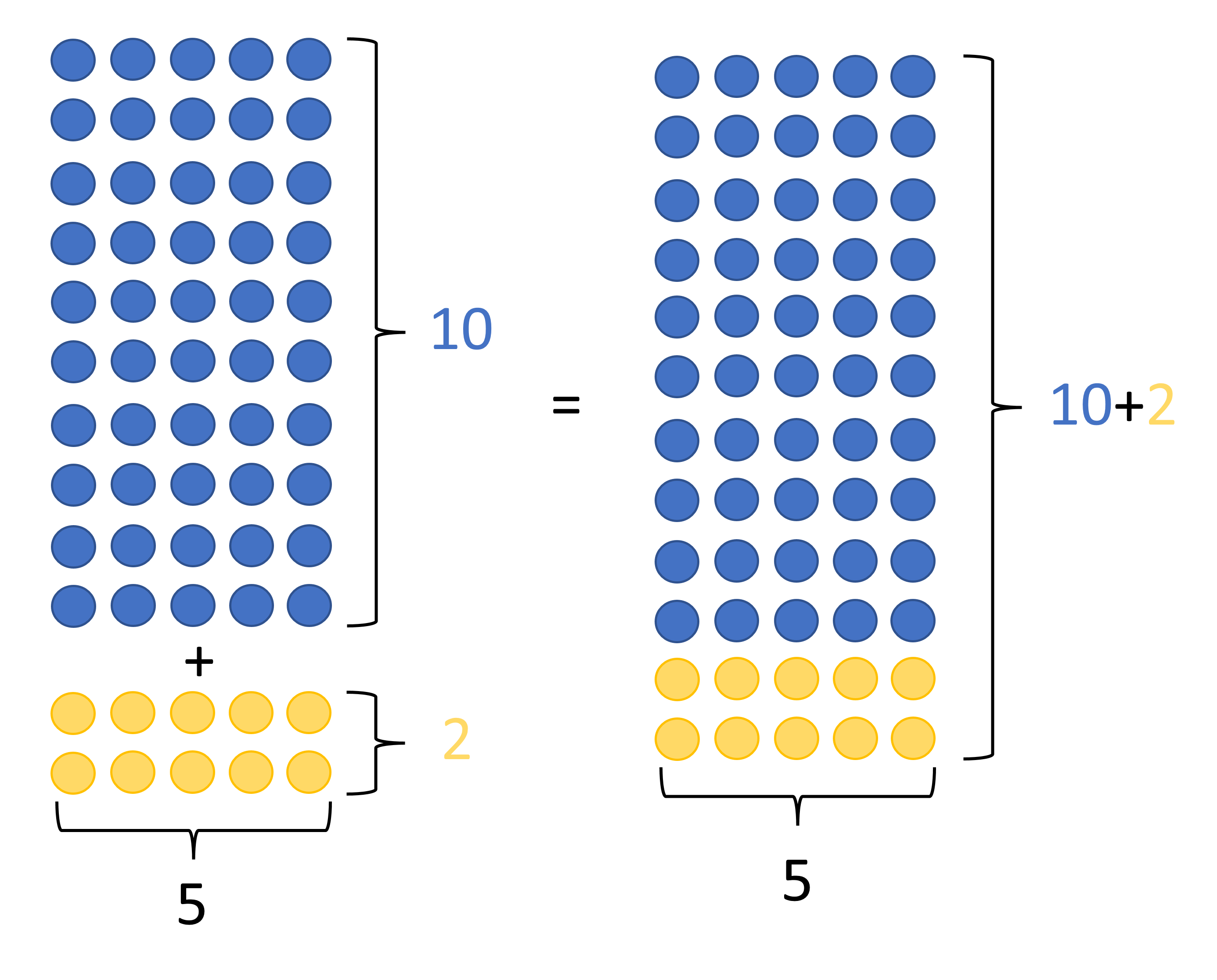
Das Distributivgesetz wird definiert als
Bei dieser Rechnung von links nach rechts wurden die Klammern aufgelöst, dieser Vorgang wird "Ausmultiplizieren" genannt. Zudem gilt die Umkehrung
welche "Ausklammern" genannt wird, da der gemeinsame Faktor vor die Klammer geholt wird.
Befindet sich in den Klammern eine Multiplikation oder Division, gilt das Distributivgesetz nicht. Wie Du in diesem Fall die Klammer auflösen kannst, erfährst Du in dem Artikel "Klammer auflösen".
Distributivgesetz beim Rechnen mit "geteilt durch" statt "mal"
Bei einer Division kann man das Distributivgesetz auf den Dividenden anwenden, nicht jedoch auf den Divisor:
Formel | Beispiel |
|---|---|
und ebenso | |
ABER: | aber |
Distributivgesetz beim Rechnen mit Variablen
Ausmultiplizieren von Klammern
Ausklammern eines Faktors
einfach umgekehrt wie beim Ausmultiplizieren)
| ↓ Gemeinsamen Faktor suchen: | ||
| ↓ Ausklammern | ||
Distributivgesetz erklärt
In diesem Video wird das Distributivgesetz erklärt und mithilfe von Beispielen vertieft.
Laden
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Anwenden der Rechengesetze
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
