1 Übersicht
Inhalt des Kurses
Du lernst, wie du konstruierbare Dreiecke konstruieren kannst. Am Ende des Kurses kannst du aus gegebenen Werten und mit Zirkel und Lineal das zugehörige Dreieck konstruieren.
Du findest hier zu jedem Kongruenzsatz eine zugehörige Schritt-für-Schritt Anleitung.
Vorkenntnisse
Du weißt, was ein Dreieck, eine Strecke und ein Winkel ist.
Du kennst die Kongruenzsätze für Dreiecke und kannst sie auf Aufgaben anwenden.
Du weißt, welche Dreiecke man konstruieren kann und wie man anhand der Angaben erkennt, ob sie konstruierbar sind oder nicht.
Wenn du das nochmal wiederholen willst oder Probleme damit hast, dann mache erst den Kurs zu den "Konstruierbaren Dreiecken".
Kursdauer
Dieser Kurs dauert ca. 90min.
2 Motivation
Die Konstruktion nur mit Zirkel und Lineal ist ein sehr altes Problem in der Geschichte der Mathematik. Man versuchte schon seit dem 5. Jahrhundert vor Christus geometrische Figuren nur mit diesen zwei einfachen Werkzeugen zu zeichnen.
Unter anderem können mit der Konstruktion von Vielecken und bestimmten geometrischen Zusammenhängen auch komplexe Rechnungen geführt werden.
Die Quadratur des Kreises birgt dabei die wohl berühmteste Berechnung durch eine Konstruktion: Es soll der Flächeninhalt des Kreises bestimmt werden, indem man ein Quadrat mit demselben Flächeninhalt konstruiert und von diesem die Seitenlänge misst.
Die Dreieckskonstruktion spielte vor allem eine Rolle um Distanzen zwischen entfernten Objekten (oder Städten) zu bestimmen.

3 Was ist Konstruieren eigentlich?
Konstruieren bedeutet eine exakte Zeichnung einer Figur anzufertigen und dabei nur die “euklidischen Werkzeuge” Zirkel und Lineal zu verwenden.
Man nutzt dazu immer Schnittpunkte, der gezeichneten Formen. Also Schnittpunkt von Kreis-Kreis, von Gerade-Gerade oder von Kreis-Gerade, um auf die zu bestimmenden Formen zu kommen.
Das Lineal dient dabei nur dazu, um eine gerade Linie zu ziehen. Der Zirkel dient dazu, genaue Strecken abzumessen.
Das besondere am Konstruieren ist, dass die Zeichnungen genauer werden, als wenn man sie mit einem Geodreieck anfertigen würde!
Für die Konstruktion sind einige Größen der Figur angegeben, mit denen man dann die Figur eindeutig konstruieren kann.
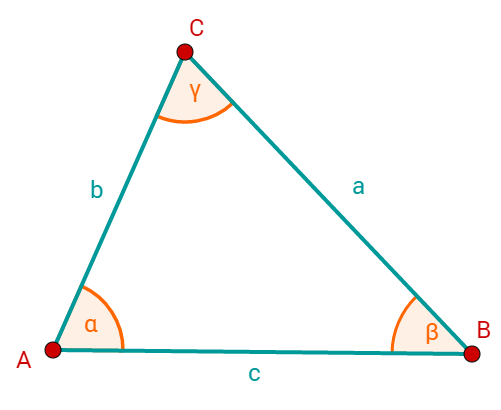
Bei einem Dreieck sind die möglichen angegebenen Größen die drei Winkel und die drei Seiten .
Beachte, dass bei Dreiecken die Seite immer gegenüber dem Punkt und dem Winkel liegt.
4 Basismethoden des Konstruierens
Jetzt kommen wir zum Konstruieren.
Dazu ein paar Basics:
Benutze ein weißes Blatt Papier, du benötigst keine Kästchen
Benutze immer einen spitzen Bleistift, nur so wird deine Zeichnung genau!
Du benötigst außerdem noch einen (möglichst ebenfalls gespitzten) Zirkel und ein Lineal
Dreiecke werden immer entgegen dem Uhrzeigersinn beschriftet, die Seite liegt dabei dem Punkt genau gegenüber. Der Winkel liegt direkt beim Punkt .
Mit den zwei Werkzeugen Lineal und Zirkel kann man jeweils besondere Tätigkeiten machen:
Lineal: eine Gerade oder eine direkte Verbindung zweier Punkte zeichnen
Zirkel: alle Punkte mit Radius r um einen bestimmten Punkt (den Einstechpunkt) werden gekennzeichnet. So kann man bestimmte Längen übertragen.

5 Basismethoden: Übertragen einer Strecke
Es gibt zwei verschiedene Möglichkeiten, die gegebenen Strecken in deine Zeichnung zu übertragen.
Welche Methode du benutzen solltest kommt dabei auf deine Schule und deinen Lehrer an. Frage ihn dazu am besten!
Die erste Methode funktioniert folgendermaßen:
Ziehe dazu im Applet den Punkt nach rechts, um einen Schritt voran zu kommen.
Die zweite Methode funktioniert so:
6 Basismethode: Winkel übertragen
Die angegebenen Winkel kannst du auch mithilfe unterschiedlicher Methoden übertragen. Bei der einen benutzt du wie gewohnt dein Geodreieck, bei der anderen überträgst du den vorgegebenen Winkel mithilfe Zirkel und Lineal.
Prinzipiell bekommst du mit beiden Methoden dasselbe Ergebnis. Welche Methode du benutzen solltest hängt von deiner Schule und deinem Lehrer ab. Frag ihn am besten!
Die Standardmethode mit Geodreieck funktioniert wie folgt:
Die Methode nur mit Zirkel und Lineal funktioniert so:
7 Basismethode: Konstruktionsprotokoll verfassen
Ein Konstruktionsprotokoll beschreibt die einzelnen Konstruktionsschritte und ist dafür da, dass du oder andere Personen die Konstruktion zu einem späteren Zeitpunkt nachverfolgen können.
Es ist wichtig, dass du dieses Protokoll so schreibst, dass jeder einzelne Schritt später nachgemacht werden könnte.
Gleichzeitig soll das Protokoll aber so kurz wie möglich werden, damit du dich nicht lange mit Beschreibungen aufhalten musst.
Bei den Beschreibungen der Konstruktionen im Folgenden wirst du immer eine lange, ausführliche Konstruktionsbeschreibung und am Ende jedes Applets ein kurzes Konstruktionsprotokoll finden. Dieses kurze Konstruktionsprotokoll ist ausreichend, um die Konstruktion später nachvollziehen zu können. Dieses Protokoll solltest du auch immer führen um einen Überblick zu behalten!
8 Konstruieren der Dreiecke
Auf den folgenden Folien findest du nun Applets, die dir zeigen, wie man Dreiecke mithilfe von den Kongruenzsätzen Schritt für Schritt konstruieren kann.
Wie man gegebene Strecken und Winkel überträgt, findest du auf den vorherigen Folien ausführlich. Diese Schritte werden nun nicht mehr so ausführlich behandelt.
SSS-Satz
SWS-Satz
WSW-Satz
SsW-Satz
9 Dreieckskonstruktion mithilfe des SSS-Satzes
Im Applet findest du die Anleitung für eine Konstruktion, wenn du alle drei Seiten des Dreiecks gegeben hast.
Ziehe den schwarzen Punkt nach rechts, um einen Schritt weiter zu kommen.
10 Dreieckskonstruktion mithilfe des SWS-Satzes
Im Applet findest du die Anleitung für eine Konstruktion, wenn du zwei Seiten und den dazwischenliegenden Winkel des Dreiecks gegeben hast.
Ziehe den schwarzen Punkt nach rechts, um einen Schritt weiter zu kommen.
Diese Anleitung ist exemplarisch für die Seiten und und den Winkel , du kannst es aber auch auf jede andere Kombination des SWS-Satzes übertragen!
11 Dreieckskonstruktion mithilfe des WSW-Satzes
Im Applet findest du die Anleitung für eine Konstruktion, wenn du eine Seite und die zwei anliegenden Winkel des Dreiecks gegeben hast.
Ziehe den schwarzen Punkt nach rechts, um einen Schritt weiter zu kommen.
Diese Anleitung ist exemplarisch für die Seite c und die Winkel und du kannst es aber auch auf jede andere Kombination des WSW-Satzes übertragen!
12 Dreieckskonstruktion mithilfe des SsW-Satzes
Im Applet findest du die Dreieckskonstruktion, wenn du zwei Seiten und einen anliegenden Winkel gegeben hast.
Der Winkel muss dabei an der kürzeren Seite anliegen, bzw. gegenüber der langen Seite sein, ansonsten ist das Dreieck nicht eindeutig konstruierbar!
Die Konstruktion wurde exemplarisch für die Seiten , und den Winkel gemacht, kann aber genauso für jede andere Kombination an Größen durchgeführt werden.
13 Übung: Dreiecke konstruieren
Laden
