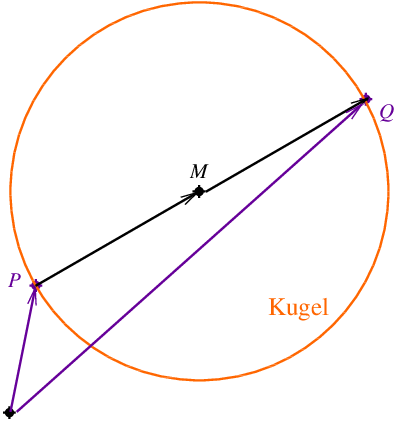
Eine Kugel besitzt den Mittelpunkt . Der Punkt liegt auf der Kugel.
a) Der Punkt liegt ebenfalls auf der Kugel, die Strecke verläuft durch deren Mittelpunkt. Ermitteln Sie die Koordinaten von . (3 BE)
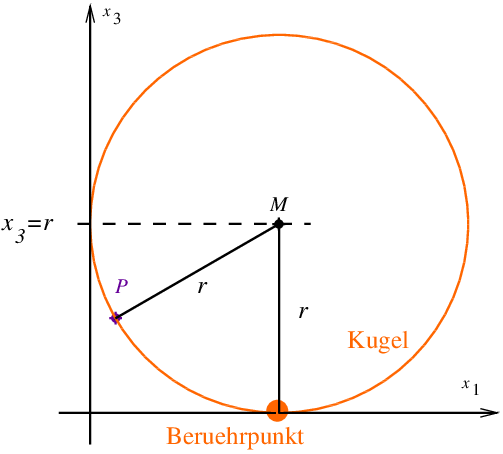
b) Weisen Sie nach, dass die Kugel die -Ebene berührt. (2 BE)