Hat eine Funktionenschar einen gemeinsamen Punkt, durch den alle Funktionen der Schar laufen, so spricht man von einem Funktionenbündel.
Diesen gemeinsamen Punkt hat eine Funktionenschar immer dann, wenn für ein bestimmtes der Parameter der Schar wegfällt. Bei diesem -Wert liegt dann dieser gemeinsame Punkt.
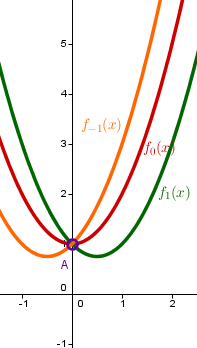
Überprüfung auf gemeinsame Punkte
Eindeutiger Schnittpunkt
Eine Funktionenschar kann einen gemeinsamen Schnittpunkt haben. Dafür muss der Parameter aber für ein aus dem Funktionsterm wegfallen.
Beispiel
Gegeben sei die Funktionenschar
Hat diese Schar einen gemeinsamen Punkt?
Ja, denn bei fällt der Parameter k weg und es bleibt nur
Daraus erhält man auch sofort den gemeinsamen Punkt unabhängig von .

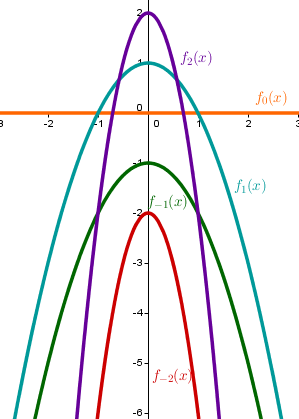
Kein eindeutiger Schnittpunkt
Beispiel
Gegeben sei die Funktionenschar
Hat diese Schar einen gemeinsamen Punkt?
Das ist nicht der Fall.
Das nebenstehende Bild zeigt die Funktionsgraphen von für
Hier sieht man, dass es keinen eindeutigen Schnittpunkt gibt.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
