Gegeben ist die in {0} definierte Funktion ,
welche die Nullstellen und hat.
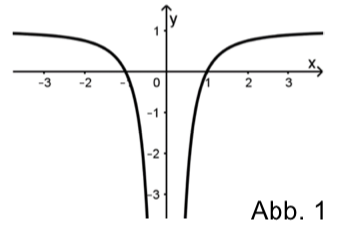
Abbildung1 zeigt den Graphen von , der symmetrisch bezüglich der y-Achse ist.
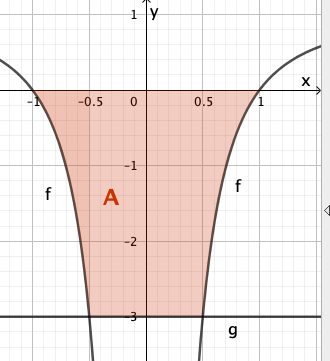
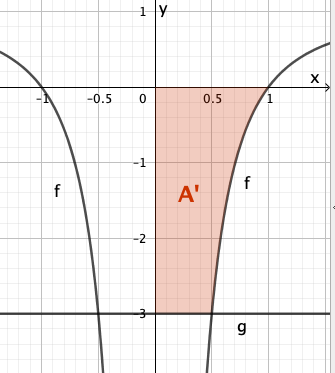
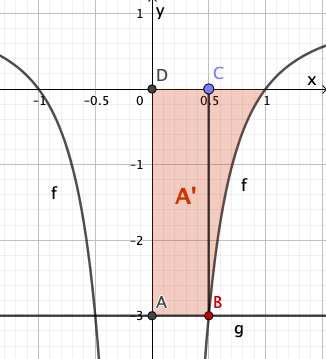
Weiterhin ist die Gerade mit der Gleichung gegeben.
a)
Zeigen Sie, dass einer der Punkte, in denen den Graphen von schneidet, die x-Koordinate hat.
b)
Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von , die x-Achse und die Gerade einschließen.