Stochastik, Teil B, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Ein Unternehmen organisiert Fahrten mit einem Ausflugsschiff, das Platz für 60 Personen bietet.
Betrachtet wird eine Fahrt, bei der das Schiff voll besetzt ist. Unter den Fahrgästen befinden sich Erwachsene, Jugendliche und Kinder. Die Hälfte der Fahrgäste isst während der Fahrt ein Eis, von den Erwachsenen nur jeder Dritte, von den Jugendlichen und Kindern 75 %. Berechnen Sie, wie viele Erwachsene an der Fahrt teilnehmen.
(3 BE)
- 2
Möchte man an einer Fahrt mit einem Ausflugsschiff, das Platz für 60 Fahrgäste bietet, teilnehmen, so muss man dafür im Voraus eine Reservierung vornehmen, ohne dabei schon den Fahrpreis bezahlen zu müssen. Erfahrungsgemäß erscheinen von den Personen mit Reservierung einige nicht zur Fahrt. Für die zur Verfügung stehenden Plätze lässt das Unternehmen deshalb bis zu Reservierungen zu. Es soll davon ausgegangen werden, dass für jede Fahrt tatsächlich Reservierungen vorgenommen werden. Erscheinen mehr als Personen mit Reservierung zur Fahrt, so können nur von ihnen daran teilnehmen; die übrigen müssen abgewiesen werden.
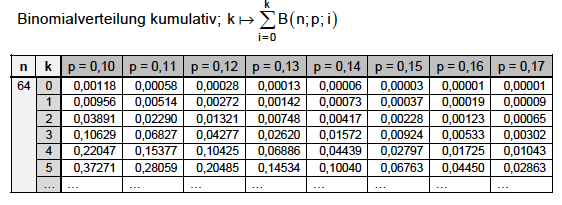
Die Zufallsgröße beschreibt die Anzahl der Personen mit Reservierung, die nicht zur Fahrt erscheinen. Vereinfachend soll angenommen werden, dass binomialverteilt ist, wobei die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit Reservierung nicht zur Fahrt erscheint, beträgt. Die am Ende abgebildete Tabelle ergänzt das zugelassene Tafelwerk.
a)
(1 BE)
Geben Sie einen Grund dafür an, dass es sich bei der Annahme, die Zufallsgröße ist binomialverteilt, im Sachzusammenhang um eine Vereinfachung handelt.
b)
(3 BE)
Bestimmen Sie die Wahrscheinlichkeit dafür, dass keine Person mit Reservierung abgewiesen werden muss.
c)
(3 BE)
Für das Unternehmen wäre es hilfreich, wenn die Wahrscheinlichkeit dafür, mindestens eine Person mit Reservierung abweisen zu müssen, höchstens ein Prozent wäre. Dazu müsste die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit Reservierung nicht zur Fahrt erscheint, mindestens einen bestimmenten Wert haben. Ermitteln Sie diesen Wert auf ganze Prozent genau.
Das Unternhmen richtet ein Online-Portal zur Reservierung ein und vermutet, dass dadurch der Anteil der Personen mit Reservierung, die zur jeweiligen Fahrt nicht erscheinen, zunehmen könnte. Als Grundlage für die Entscheidung darüber, ob pro Fahrt künftig mehr als Reservierungen zugelassen werden, soll die Nullhypothese "Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit Reservierung nicht zur Fahrt erscheint, beträgt höchstens ." mithilfe einer Stichprobe von Personen mit Reservierung auf einem Signifikanzniveau von getestet werden. Vor der Durchführung des Tests wird festgelegt, die Anzahl der für eine Fahrt möglichen Reservierungen nur dann zu erhöhen, wenn die Nullhypothese aufgrund des Testergebnisses abgelehnt werden müsste.
d)
(5 BE)
Ermitteln Sie die zughörige Entscheidungsregel.
e)
(3 BE)
Entscheiden Sie, ob bei der Wahl der Nullhypothese eher das Interesse, dass weniger Platz frei bleiben sollen, oder das Interesse, dass nicht mehr Personen mit Reservierung abgewiesen werden müssen, im Vordergrund stand. Begründen Sie Ihre Entscheidung.
f)
(2 BE)
Beschreiben Sie den zugehörigen Fehler zweiter Art sowie die daraus resultierende Konsequenz im Sachzusammenhang.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
