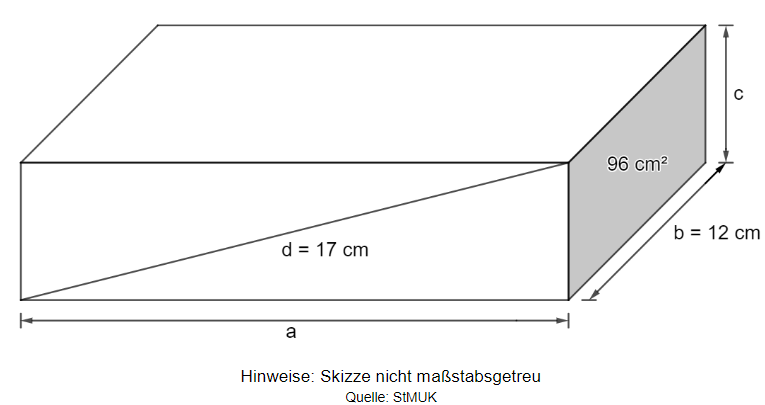
Die Kante des dargestellten Quaders hat eine Länge von , die eingezeichnete Diagonale eine Länge von und seine grau markierte Seitenfläche einen Flächeninhalt von .
Berechne die Oberfläche des Quaders.
cm²
Die Kante des dargestellten Quaders hat eine Länge von , die eingezeichnete Diagonale eine Länge von und seine grau markierte Seitenfläche einen Flächeninhalt von .
Berechne die Oberfläche des Quaders.
