Bestimme den Flächeninhalt der folgenden Kreissektoren. Gib deine Lösungen auf zwei Stellen nach dem Komma gerundet ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Formel für die Berechnung der Kreissektorfläche
Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen. Rechne anschließend den Term aus:
Hast du eine Frage oder Feedback?
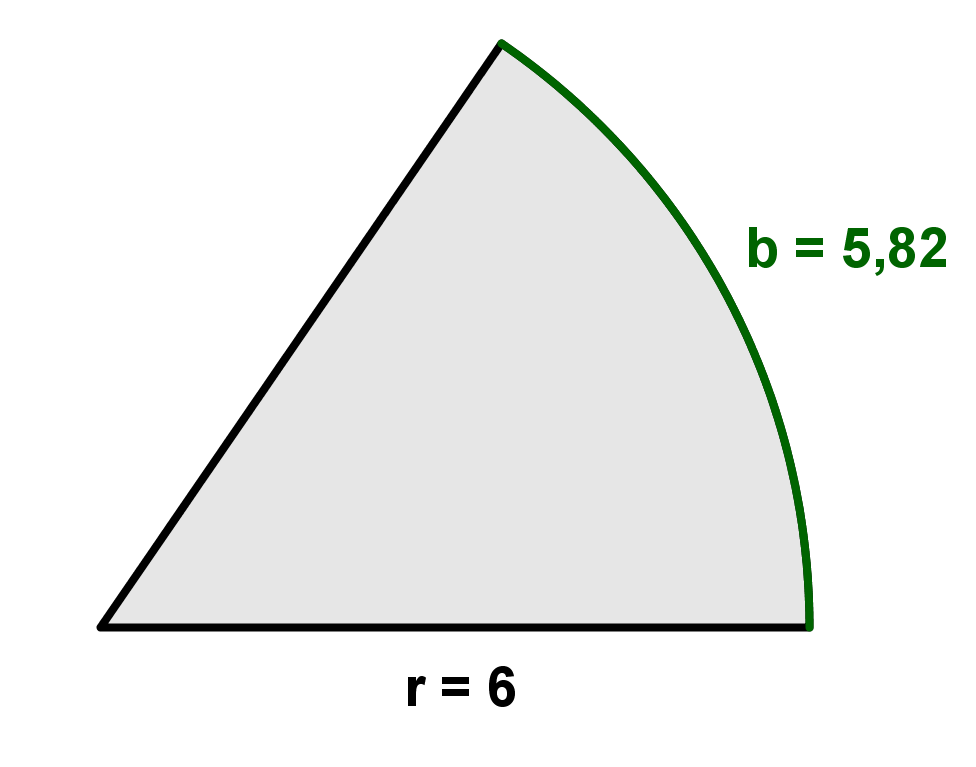
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Kreissektors
Setze die Bogenlänge und den Radius in die Formel ein, um den Flächeninhalt zu bestimmen.
Hast du eine Frage oder Feedback?
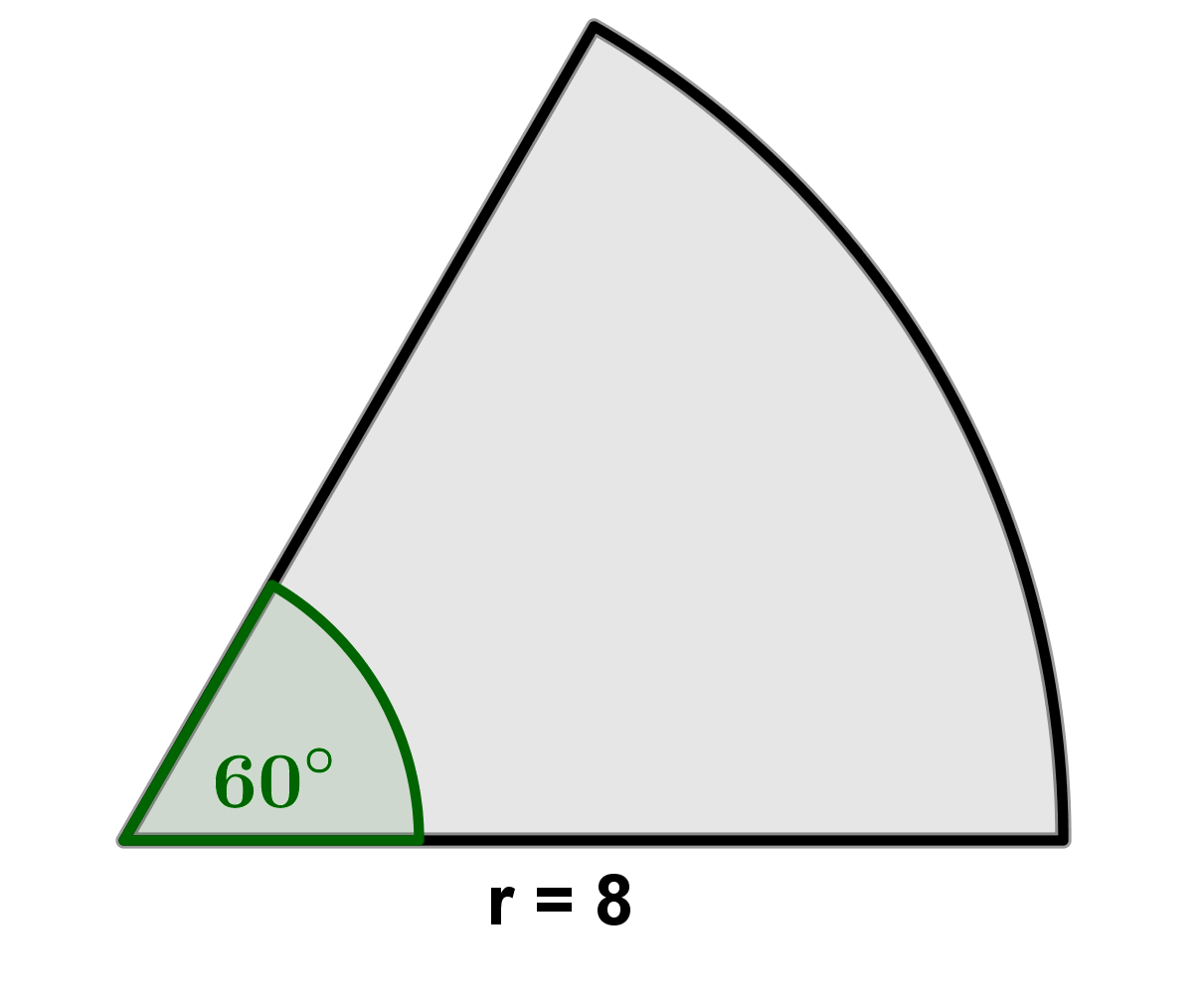
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Kreissektors
Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen.
Rechne aus und runde auf zwei Stellen nach dem Komma.
Hast du eine Frage oder Feedback?
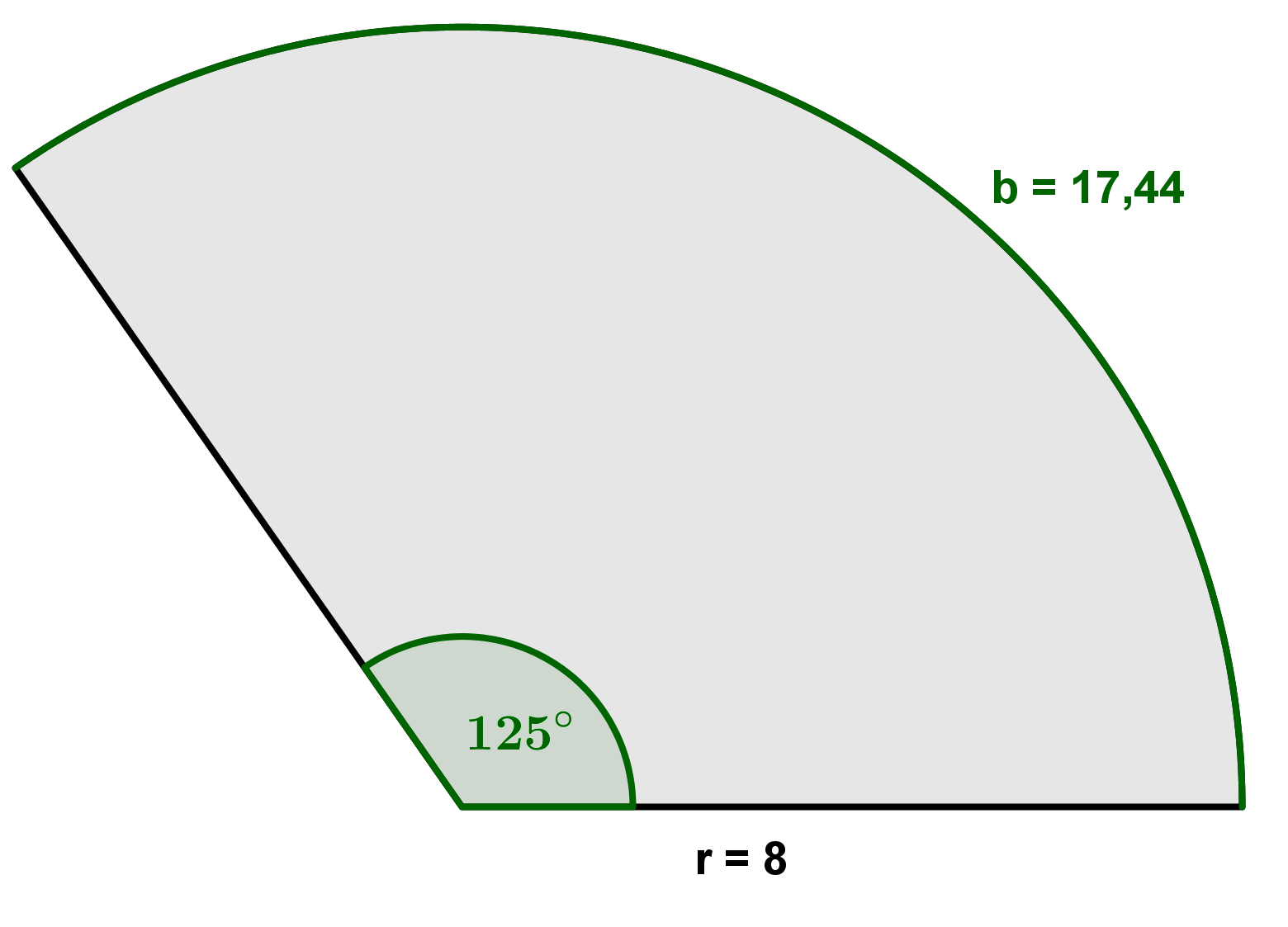
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Kreissektors
1. Möglichkeit: Mit dem Radius und dem Mittelpunktswinkel
Benutze die Formel, in der und vorkommen:
Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen.
Berechne.
2. Möglichkeit: Mit dem Radius und der Länge des Kreisbogens
Benutze die Formel, in der und vorkommen:
Setze die Bogenlänge und den Radius in die Formel ein, um den Flächeninhalt zu bestimmen.
Die kleine Abweichung zum vorherigen Ergebnis kommt vom Runden der Länge des Kreisbogens.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
