Aufgaben zu Beziehungen zwischen den besonderen Vierecksarten

Hier findest du Verständnisaufgaben zur Beziehung zwischen den besonderen Vierecken. Wiederhole wichtige Grundlegen und entdecke neues Wissen!

1
Kreuze die zutreffenden Aussagen an
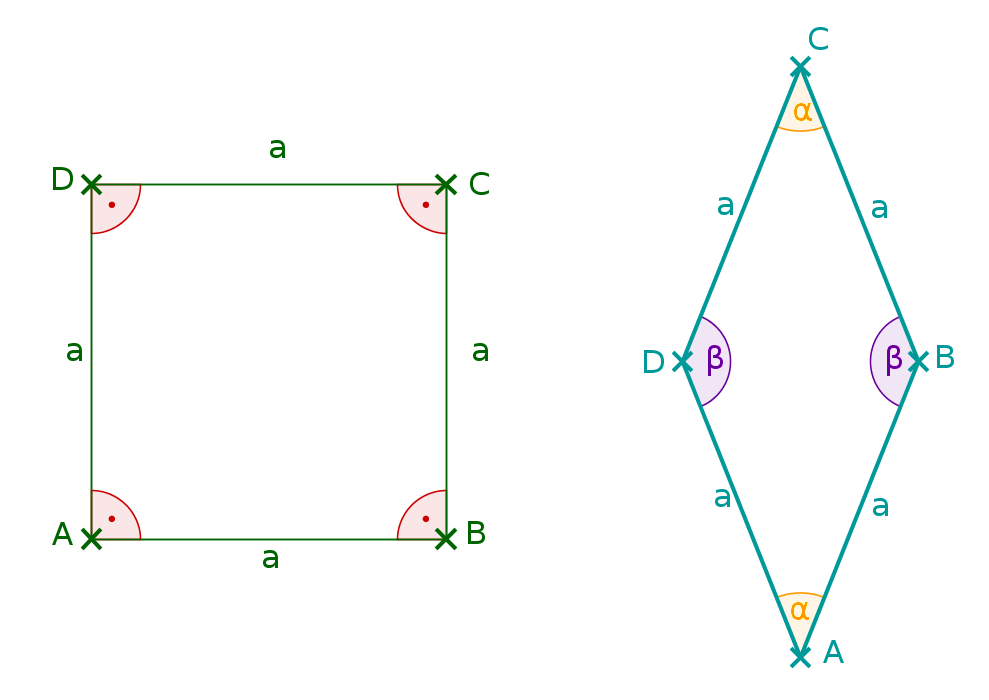
1. Welche Vierecke haben zwei Symmetrieachsen?
  Raute
  Rechteck
  Parallelogramm
  symmetrischer Drachen
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Haus der Vierecke
  Tipp: Schau dir am Besten das Haus der Vierecke nochmal an!
  Teile Deine Lösungen mit uns!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bei welchen Vierecken sind mindestens zwei Winkel gleich groß?
  Quadrat
  symmetrischer Drache
  Parallelogramm
  allgemeines Trapez
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Haus der Vierecke
  Parallelogramm, Quadrat und symmetrischer Drache.
  Tipp: Schau dir am Besten das Haus der Vierecke nochmal an!
  Teile deine Lösungen mit uns!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Welche Eigenschaften haben sowohl das Quadrat als auch das Parallelogramm?
  gegenüberliegende Seiten sind parallel
  die Vierecke sind punktsymmetrisch
  benachbarte Winkel sind gleich groß
  die Vierecke sind achsensymmetrisch
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Haus der Vierecke
  Tipp: Schau dir am Besten das Haus der Vierecke nochmal an!
  Gerne kannst du deine Lösungen mit uns teilen!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Was ist ein Rechteck gleichzeitig immer auch?
  allgemeines Trapez
  Parallelogramm
  Drachenviereck
  Quadrat
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Haus der Vierecke
  Tipp: Schau dir am Besten das Haus der Vierecke nochmal an!
  Gerne kannst du deine Lösungen mit uns teilen!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Prüfe folgende Aussagen auf ihren Wahrheitsgehalt. Begründe kurz oder gib ein Gegenbeispiel an.
1. Jede Raute ist ein Parallelogramm.
  Ja!
  Nein!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierecke
  Die Aussage stimmt.
  Nach Definition ist die Raute ein spezielles Parallelogramm, nämlich eines, bei dem mindestens eine der Diagonalen Symmetrieachse der Figur ist.
  Somit ist jede Raute ein Parallelogramm.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Jedes Parallelogramm ist eine Raute.
  Nein!
  Ja!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierecke
  Die Aussage stimmt nicht.
  Eine Raute ist symmetrisch bzgl ihrer Diagonalen. Dies ist bei einem Parallelogramm nicht zwingend der Fall.
  Die Abbildung zeigt zwei Parallelogramme, von denen das linke eine Raute ist und das rechte nicht:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
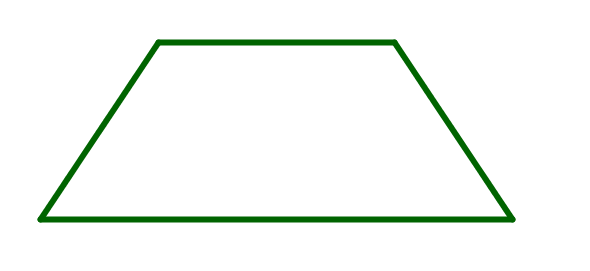
3. Jedes Parallelogramm ist ein Trapez.
  Ja!
  Nein!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierecke
  Die Aussage stimmt. Jedes Parallelogramm ist ein Trapez.
  Dies folgt unmittelbar aus der Definition eines Parallelogramms. In einem Parallelogramm sind alle gegenüberliegenden Seiten zueinander parallel. Für ein Trapez gilt die schwächere Bedingung, dass mindestens zwei gegenüberliegende Seiten zueinander parallel sind.
  Somit ist ein Parallelogramm ein spezielles Trapez.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Jedes Viereck mit vier gleich langen Seiten ist ein Quadrat.
  Nein!
  Ja!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierecke
  Das ist falsch! Ein Viereck mit vier gleich langen Seiten heißt Raute. In einem Quadrat sind zusätzlich alle Winkel gleich groß.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Jedes Quadrat ist auch ein Trapez, Parallelogramm und ein Rechteck.
  Ja!
  Nein!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierecke
  Das ist richtig!
  Ein Trapez hat zwei gegenüberliegende parallele Seiten.
  In einem Parallelogramm sind alle gegenüberliegenden Seiten zueinander parallel.
  Ein Rechteck ist ein Viereck mit vier gleichgroßen Innenwinkeln.
  All diese Eigenschaften treffen ebenfalls auf ein Quadrat zu.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Die Summe aller Innenwinkel in einem Viereck ist $380°$ .
  Nein!
  Ja!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Viereck
  Das ist falsch! Jedes Viereck hat eine Winkelsumme von $360°$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Wähle die richtige Antwort aus.
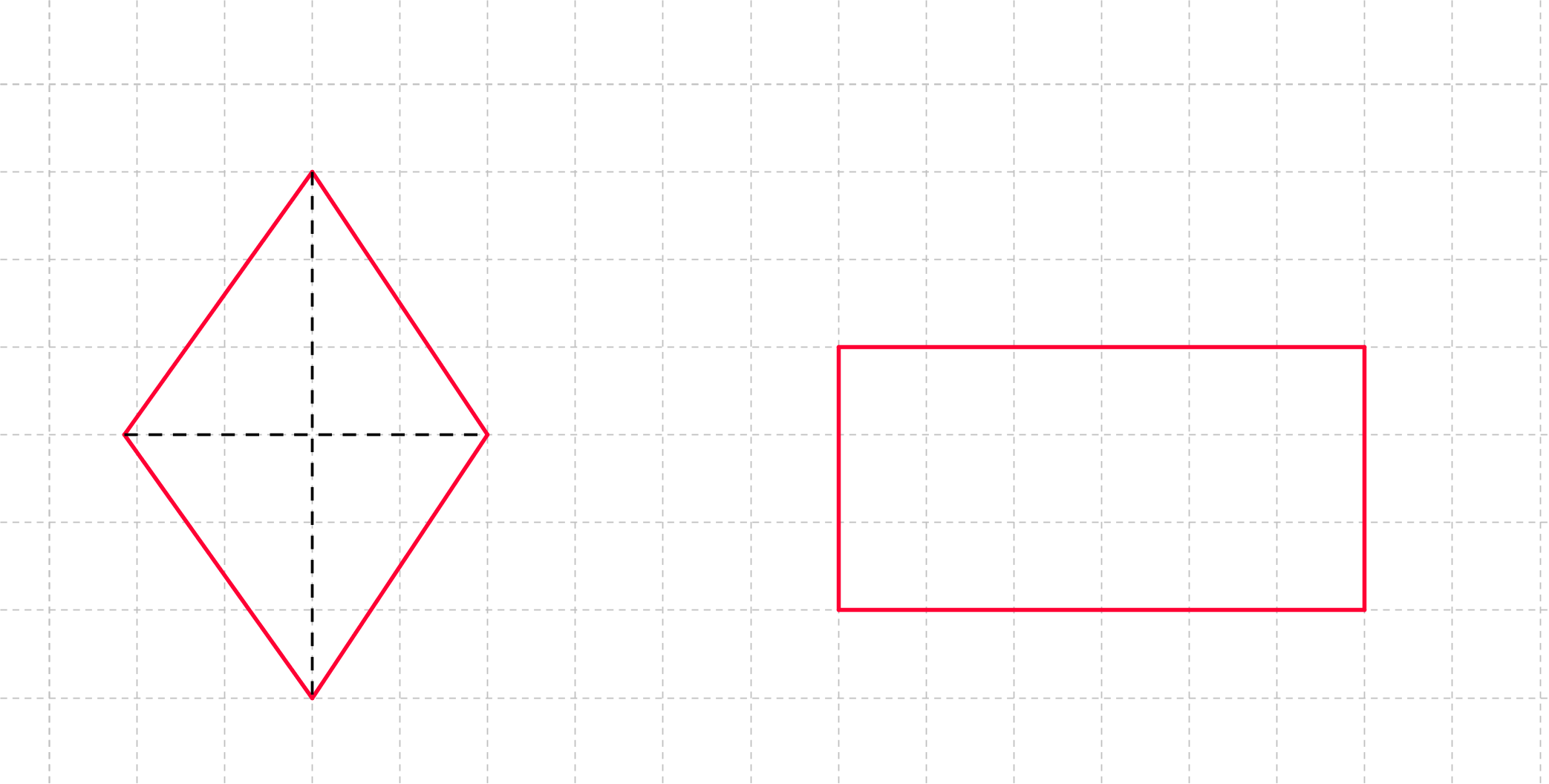
1. Welches der folgenden Vierecke ist kein Parallelogramm?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelogramm
  In einem Parallelogramm sind die gegenüberliegenden Seiten parallel. Das ist beim Trapez in dieser Aufgabe nicht so. Die rechte und linke Seite vom Trapez sind nicht parallel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Benutze deine Formelsammlung oder schau im Internet nach (siehe Grundwissen!). Präge dir die Merkmale gut ein, denn Figuren und ihre Eigenschaften sind Grundwissen in der Geometrie.
4
Die Ordnungskraft der Mittelpunkte
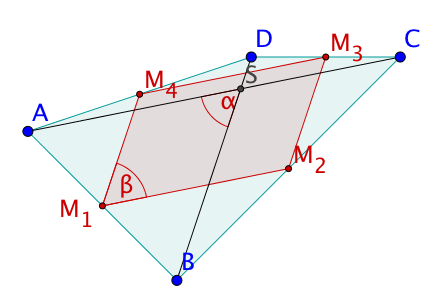
Ein allgemeines Viereck $ABCD$ . Die Seiten des Vierecks sind weder parallel noch gleich lang.
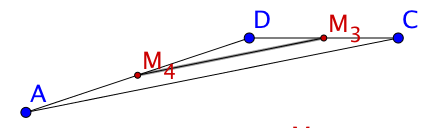
Verbindet man die Mittelpunkte der Vierecksseiten zu einem neuen Viereck, entsteht das "Mittelpunktsviereck". Das Mittelpunktsviereck ist stets ein Parallelogramm.
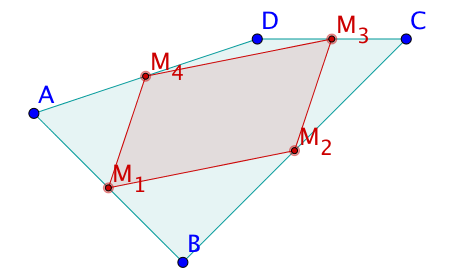
1. Begründe die "Ordnungskraft" der Seitenmittelpunkte eines Vierecks: Erkläre, warum das Mittelpunktsviereck eines beliebigen Vierecks stets ein Parallelogramm ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz
  In der Strahlensatzfigur $ADC$ (Teildreieck des Vierecks $ABCD$ ) teilen die Mittelpunkte die Strahlen $[DA$ und $[DC$ im gleichen Verhältnis 1:1. Die Seite $[M_1M_2]$ ist demnach parallel zu $[AC]$ , der Diagonalen des Vierecks.
  Gleiches gilt für die drei anderen Seiten des Mittelpunktsvierecks. Dessen Seiten sind somit paarweise parallel zu einer Diagonalen des Vierecks (und im Übrigen gerade halb so lang wie diese.)
  Das Mittelpunktsviereck ist also stets ein Parallelogramm.
  Da die Seiten des Mittelpunktsvierecks parallel zu den Diagonalen des ursprünglichen Vierecks sind, ist der spitze Eckwinkel des Mittelpunktsvierecks so groß wie der spitze Winkel, in dem sich die Diagonalen des ursprünglichen Vierecks schneiden. Also ist $\alpha=\beta$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
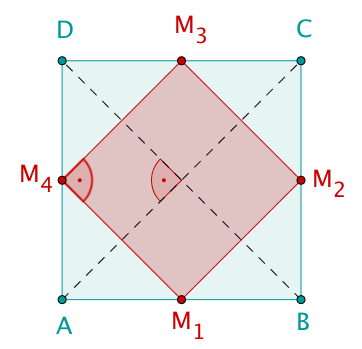
2. Von welcher Form sind die Mittelpunktsvierecke von Quadraten? Begründe deine Antwort!
  Quadrat
  Rechteck
  Raute
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat
  $\quad \quad \quad \quad$
  Das Mittelpunktsviereck eines Quadrats ist wieder ein Quadrat.
  Begründung:
  Die Diagonalen des (ursprünglichen) Quadrats sind gleich lang und stehen aufeinander senkrecht.
  Damit sind die Seiten des Mittelpunktsvierecks auch gleich lang (halb so lang wie die ursprünglichen Diagonalen) und stehen aufeinander senkrecht.
  Damit ist das Mittelpunktsviereck eines Quadrats wieder ein Quadrat.
  (Zusatz: Mit halb so großem Flächeninhalt wie das ursprüngliche Quadrat.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
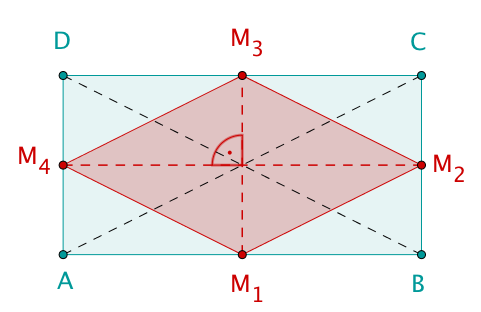
3. Von welcher Form sind die Mittelpunktsvierecke von Rechtecken? Begründe deine Anwort!
  Quadrat
  Rechteck
  Raute
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
  Das Mittelpunktsviereck eines Rechtecks ist eine Raute.
  Begründung:
  Die Diagonalen eines Rechtecks sind gleich lang, stehen aber nicht aufeinander senkrecht.
  Damit sind die vier Seiten des Mittelpunktsvierecks gleich lang. Die Eckwinkel sind aber nicht 90°.
  Damit ist das Mittelpunktsviereck eines Rechtecks eine Raute (und kein Quadrat.)
  (Zusatz: Der Flächeninhalt der Raute ist halb so groß wie der des ursprünglichen Rechtecks.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
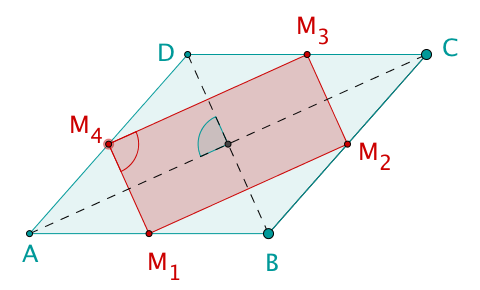
4. Von welcher Form sind die Mittelpunktsvierecke von Rauten? Begründe deine Anwort!
  Quadrat
  Rechteck
  Raute
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
  $\quad \quad \quad$
  Das Mittelpunktsviereck einer Raute ist ein Rechteck.
  Begründung:
  Die Diagonalen einer Raute stehen aufeinander senkrecht, sind aber nicht gleich lang.
  Damit sind die Eckwinkel des Mittelpunktsvierecks rechte Winkel und die Seiten paarweise verschieden lang.
  Das Mittelpunktsviereck einer Raute ist somit ein Rechteck.
  (Zusatz: Der Flächeninhalt des Rechtecks ist halb so groß wie der Flächeninhalt der ursprünglichen Raute.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉