Prüfe folgende Aussagen auf ihren Wahrheitsgehalt. Begründe kurz oder gib ein Gegenbeispiel an.
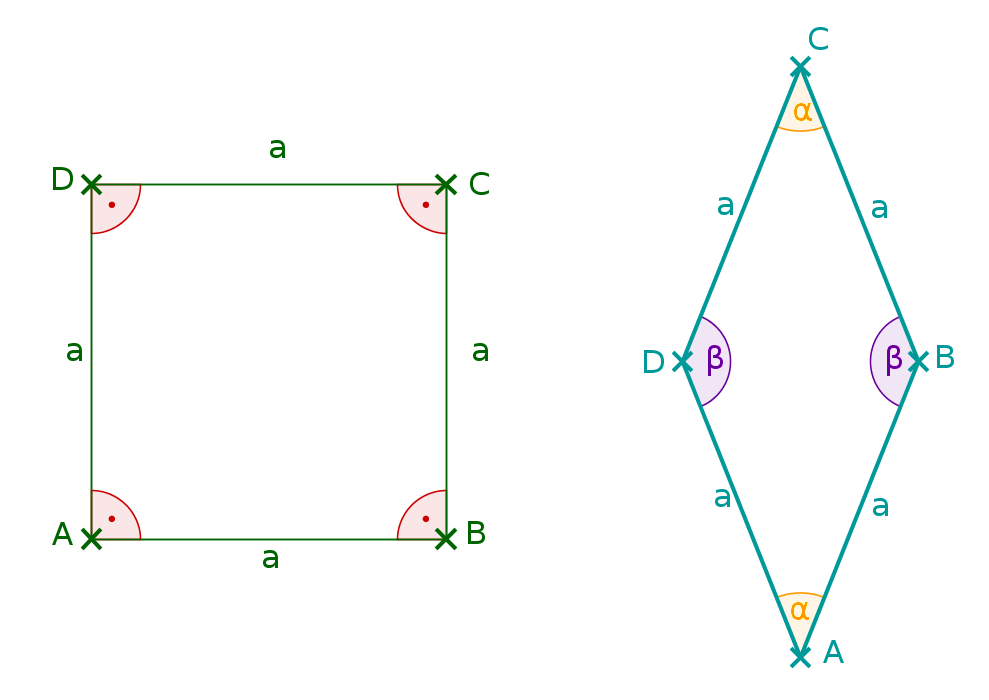
Jede Raute ist ein Parallelogramm.
Jedes Parallelogramm ist eine Raute.
Jedes Parallelogramm ist ein Trapez.
Jedes Viereck mit vier gleich langen Seiten ist ein Quadrat.
Jedes Quadrat ist auch ein Trapez, Parallelogramm und ein Rechteck.
Die Summe aller Innenwinkel in einem Viereck ist .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?