Konstrukteure gefragt
Geometrische Aufgaben löst man in der Regel durch eine Berechnung oder durch eine Konstruktion.
Eine "Konstruktion" ist eine möglichst genaue Zeichnung alleine mit den Hilfsmitteln eines Zirkels und eines Lineals. Oft darf man zur Erleichterung auch ein Geodreieck verwenden.
Löse die folgenden Aufgabenstellungen jeweils durch eine Konstruktion.
Konstruiere eine Strecke durch den Punkt P als Mittelpunkt der Strecke so, dass die Endpunkte auf g und h liegen.
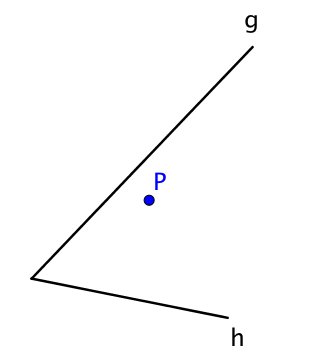
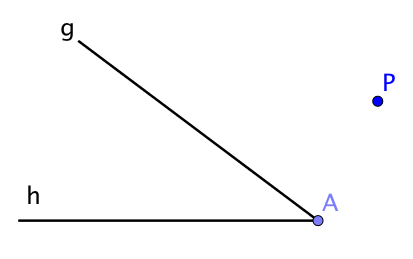
Lege eine Strecke von P aus so, dass der Endpunkt auf h liegt und die Strecke von g halbiert wird.
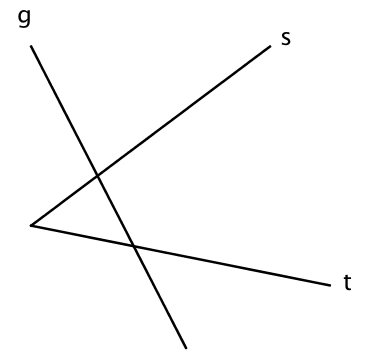
Konstruiere eine zur Geraden g parallele Strecke mit vorgegebener Länge a LE so, dass die Endpunkte der Strecke auf s und t liegen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
