Aufgaben zum Thema Ortslinien und Ortsbereiche

Hier findest du gemischte Aufgaben zu Ortslinien und Ortsbereiche im Koordinatensystem. Schaffst du sie alle?

1
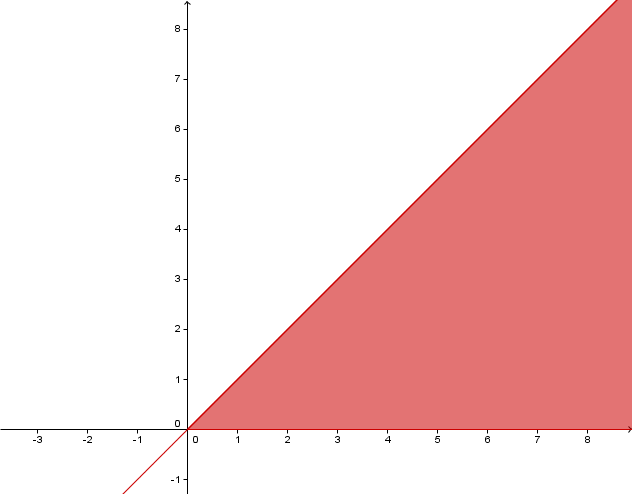
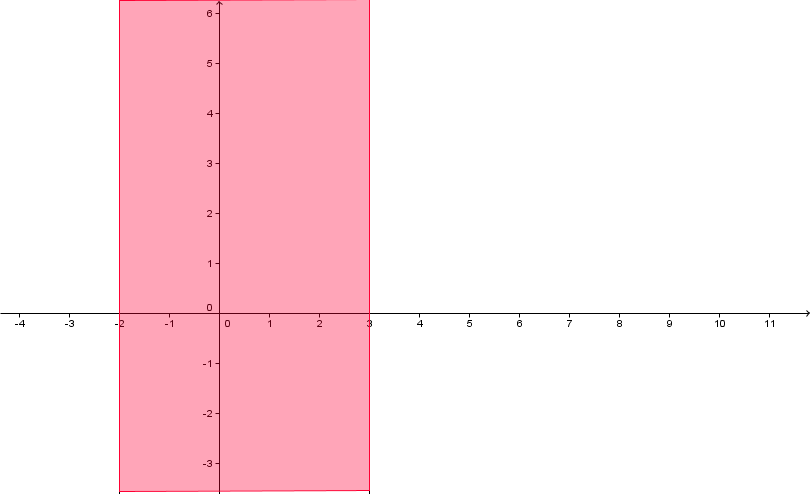
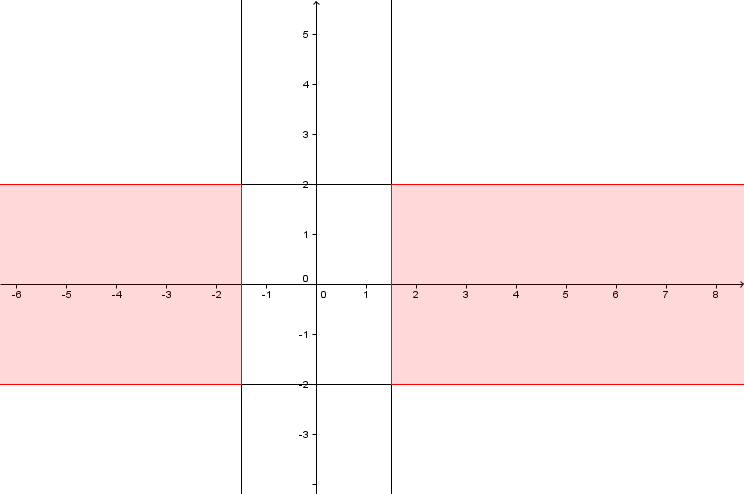
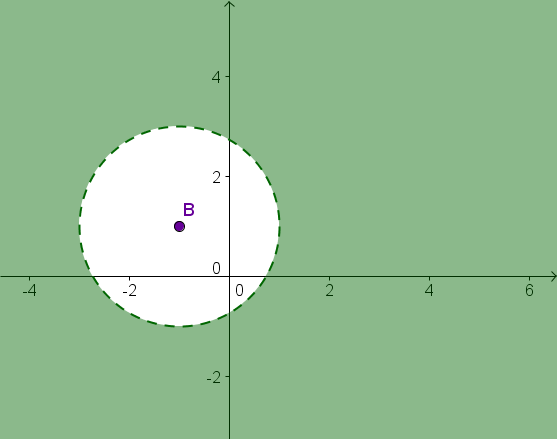
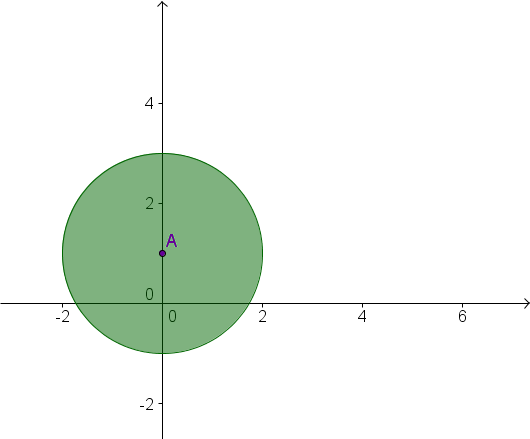
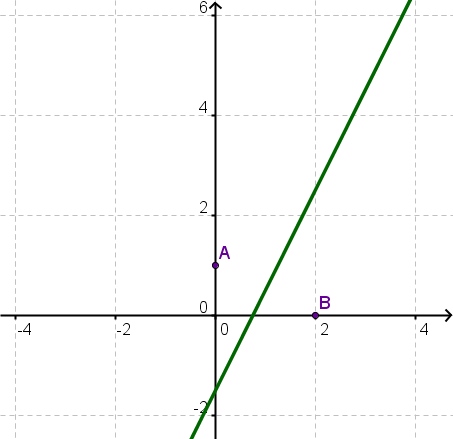
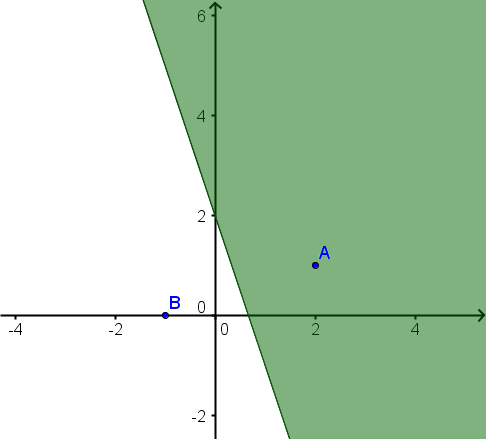
Beschreibe die gekennzeichnete Strecke bzw. Fläche.
1. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Logikverknüpfungen
  Gesucht ist eine mathematische Beschreibung der Punktmenge, die in der Zeichnung rot gekennzeichnet ist.
  Überlege dir, was das für die Koordinaten der Punkte der Strecke bedeutet.
  Das ist die Strecke, die bei x=3 nach oben geht und 2 Längeneinheiten lang ist. Die Endpunkte der Strecke gehören beide dazu.
  Es gehören alle Punkte zu dem Bereich, die einen x-Wert von 3 haben und deren y-Wert zwischen 0 und 2 liegt, wobei die y-Werte 0 und 2 auch angenommen werden dürfen.
  Beschreibe dies nun in mathematischer Formelschreibweise.
  Für alle Punkte $(x | y)$ im angegebenen Bereich gilt:
  $x = 3 \land 0 \leq y \leq 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Logikverknüpfungen
  Es gehören alle Werte zu dem Bereich,die einen x-Wert von 0 bis $\infty$ haben und deren y-Wert zwischen 0 und 2 liegt.
  Definiere den Bereich auf mathematische Weise.
  Für alle Punkte $(x | y)$ im angegebenen Bereich gilt:
  $x \geq 0 \land 0 \leq y \leq 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Logikverknüpfungen
  Es gehören alle Werte zu dem Bereich, deren y-Wert gleich oder größer ist als der zugehörige x-Wert, wobei du alle x-Werte einsetzen kannst.
  Definiere den Bereich auf mathematische Weise.
  Für alle Punkte $(x | y)$ im angegebenen Bereich gilt:
  $x \in ℝ \land y \geq x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Logikverknüpfungen
  Es gehören alle Werte zu dem Bereich, deren y-Wert gleich oder kleiner ist als der x Wert und die dabei einen größeren oder gleichen y- und x-Wert als 0 haben.
  Definiere den Bereich auf mathematische Weise.
  Für alle Punkte $(x | y)$ im angegebenen Bereich gilt:
  $y \leq x \land x \geq 0 \land y \geq 0$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Kennzeichnen Sie im Koordinatensystem alle Punkte, deren Koordinaten die gegebenen Bedingungen erfüllen.
1. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $y \leq - 1 \land x \geq 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den vorgegebenen Bereich in ein Koordinantensystem ein. Der y-Wert muss kleiner oder gleich -1 sein, während zusätzlich( $\land$ ) der x-Wert größer oder gleich 1 sein muss.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $y \in ℝ \land - 2 \leq x \leq 3$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den vorgegebenen Bereich in ein Koordinantensystem ein. Der x-Wert muss zwischen -2 und 3 liegen, während ( $\land$ ) der y-Wert jeden beliebigen Wert annehmen kann.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $x \in ℝ \land y = 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den vorgegebenen Bereich in ein Koordinantensystem ein. x kann jeden beliebigen Wert annehmen ( $ℝ$ ), während ( $\land$ ) y immer den Wert 2 hat. Das heißt der Bereich entspricht der Gerade $y = 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $0 \leq x \leq 4 \land y \geq 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den vorgegebenen Bereich in ein Koordinantensystem ein. Der x-Wert muss zwischen 0 und 4 liegen, während ( $\land$ ) der y- Wert größer als 0 sein muss.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  $| x | \geq 1,5 \land | y | \leq 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den vorgegebenen Bereich in ein Koordinantensystem ein. Der x-Wert muss einen Betrag haben, der größer als 1,5 ist, während ( $\land$ ) der y-Wert einen Betrag zwischen 0 und 2 haben muss.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $y > 0 \land x = - 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Zeichne den vorgegebenen Bereich in ein Koordinantensystem ein. Der y- Wert kann jeden Wert, der größer als 0 ist, annehmen, während ( $\land$ ) der x-Wert immer -2 ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bestimmen Sie die Lage der Punkte:
1. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  Für welche Werte von $t \in ℝ$ liegt der Punkt $P_{t} (t - 1 | \frac{1}{1 + t})$ im 1. Quadranten?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Der 1. Quadrant schließt alle Werte ein, bei denen die x und y Werte beide nicht-negativ oder Null sind.
  Überprüfe welche Bedinung erfüllt sein muss, damit dies zutrifft.
  Bedingung an die x-Koordinate
  Für die x-Werte muss also gelten: $t - 1 \geq 0$
  Nur wenn $t$ größer ist als 1, ist die $x$ -Koordinate also nicht-negativ.
  Bedingung an die y-Koordinate
  Für die y-Werte muss gelten: $\frac{1}{t + 1} \geq 0$
  $\frac{1}{t + 1} \geq 0$ , wenn der Nenner positiv ist, also $t \geq - 1$ . Der Bruch muss jedoch auch richtig definiert sein, also der Nenner nicht Null sein. Daher musst du $t = - 1$ ausschließen.
  Bedingung an den Punkt
  Somit muss
  $t \geq 1$ , damit der x-Wert größer oder gleich 0 ist
  und $t > - 1$ sein, damit der y-Wert größer oder gleich 0 ist.
  Um beide Bedingungen zu erfüllen, muss also $t \geq 1$ sein.
  $\Rightarrow$ Damit der Punkt im 1. Quadranten liegt, muss $t > 1$ sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
  Für welche Werte von $t \in ℝ$ liegt der Punkt $Q_{t} (t | t^{2} - 1)$ unterhalb der x-Achse?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Alle Punkte, die einen y-Wert haben, der kleiner als 0 ist, liegen unterhalb der x-Achse.
  Bedingung an den y-Wert
  Überprüfe, welche Bedingungen erfüllt sein müssen, damit der y-Wert kleiner 0 ist.
  $t^{2} - 1 < 0 \Leftrightarrow t^{2} < 1$
  Damit müssen die Werte zwischen 1 und -1 liegen.
  $\Rightarrow$ Der Punkt liegt unterhalb der x-Achse, wenn $t \in [- 1; 1]$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Stelle die angegebenen Punktmenge in einem Koordinatensystem dar:
1. $M = {P (x | y) | PA = 3}, wobei A (1 | 0)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortslinien und Ortsbereiche
  Die Menge M ist die Kreislinie des Kreises um A mit Radius 3.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $M = {P (x | y) | PB > 2}, wobei B (- 1 | 1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortslinien und Ortsbereiche
  Die Menge M ist das Äußere des Kreises um B mit Radius 2 ohne die Kreislinie.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $M = {Q (x | y) | QA ⩽ 2}, wobei A (0 | 1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortslinien und Ortsbereiche
  Die Menge M ist das Innere des Kreises um A mit Radius 2 einschließlich der Kreislinie.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $M = {P (x | y) | PA = PB}, wobei A (0 | 1) und B (2 | 0)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortslinien und Ortsbereiche
  Die Menge M ist die Mittelsenkrechte der Punkte A und B.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $M = {Q (x | y) | QA ⩽ QB}, wobei A (2 | 1) und B (- 1 | 0)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortslinien und Ortsbereiche
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉