Teile die Strecken im angegebenen Verhältnis und bestimme die Längen der Teilstrecken.
im Verhältnis 1:4
Für diese Aufgabe benötigst Du folgendes Grundwissen: Teilung von Strecken
Schritt 1
Zeichne eine Gerade durch den Punkt A

Schritt 2
Zeichne einen Kreis um A mit irgendeinem Radius r und markiere den Schnittpunkt des Kreises mit der Geraden.

Schritt 3
Zeichne einen Kreis mit gleich großem Radius um den gerade erhaltenen Schnittpunkt. Wiederhole dies so oft bis du insgesamt 4+1=5 Schnittpunkte hast.
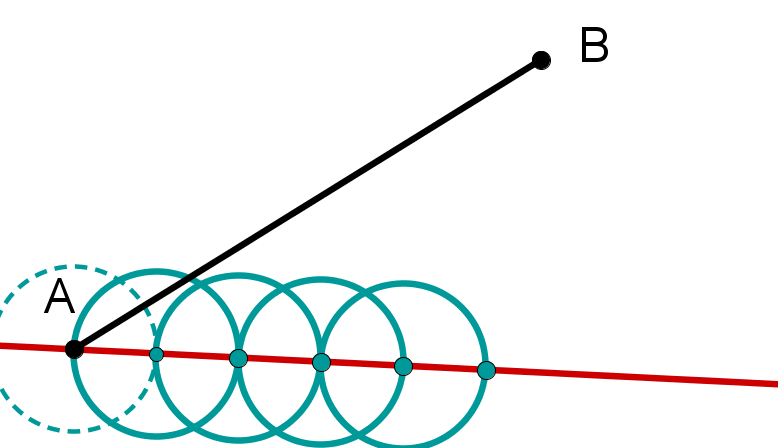
Schritt 4
Verbinde den letzten Schnittpunkt mit dem Punkt B.
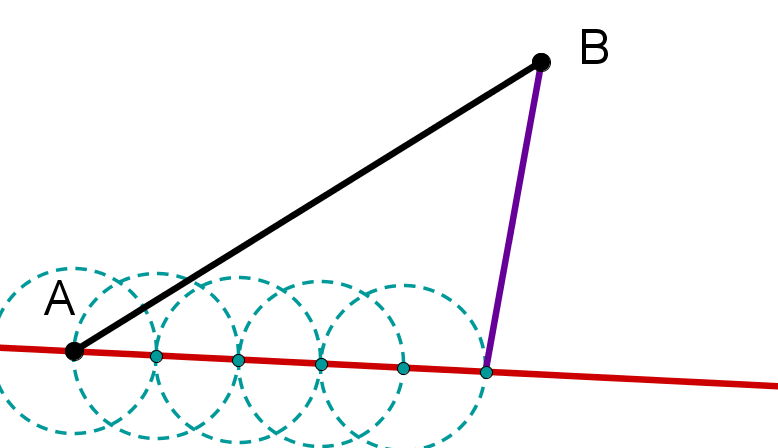
Schritt 5
Konstruiere eine Parallele zu der eben gezeichneten Strecke durch den 1. Schnittpunkt. Der Schnittpunkt dieser Parallelen mit der Strecke [AB] ist der Punkt T, der die Strecke im Verhältnis 1:4 teilt.
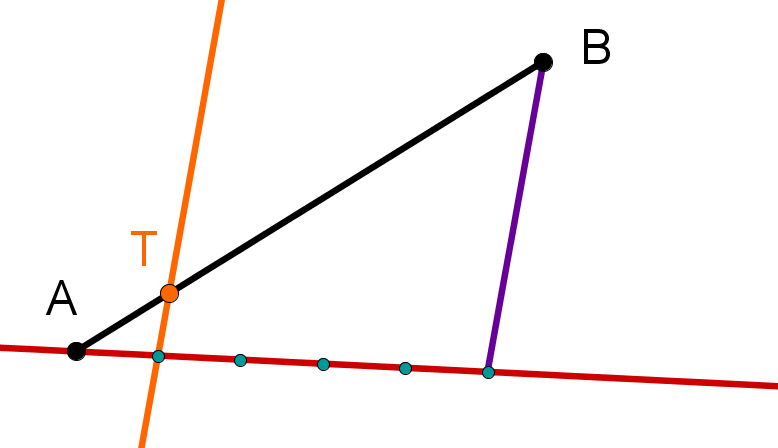
Die Länge der Teilstrecken und berechnet man mit der Formel: und
, und
Hast du eine Frage oder Feedback?
im Verhältnis 4:2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Teilung von Strecken
Schritt 1
Zeichne eine Gerade durch den Punkt C

Schritt 2
Zeichne einen Kreis um C mit irgendeinem Radius r und makiere den Schnittpunk des Kreises mit der Gerade.

Schritt 3
Zeichne einen Kreis mit gleich großem Radius um den gerade erhaltenen Schnittpunkt. Wiederhole dies so oft bis du insgesamt 4+2=6 Schnittpunkte hast.

Schritt 4
Verbinde den letzten Schnittpunkt mit dem Punkt D.
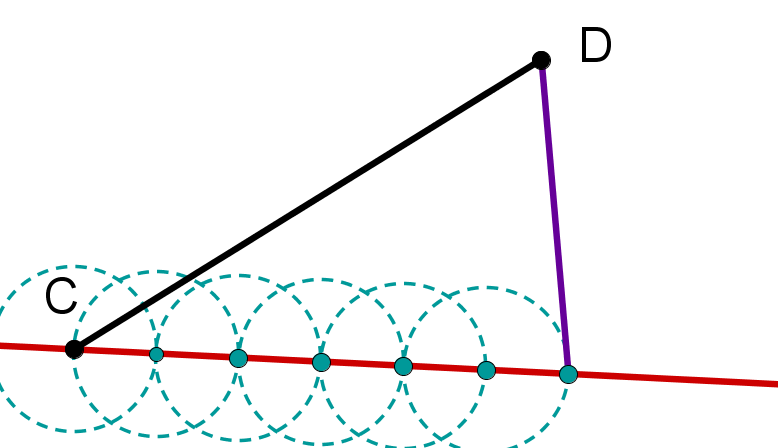
Schritt 5
Konstruiere eine Parallele zu der eben gezeichneten Strecke durch den 4. Schnittpunkt. Der Schnittpunkt dieser Parallelen mit der Strecke [CD] ist der Punkt T, der die Strecke im Verhältnis 4:2 teilt.
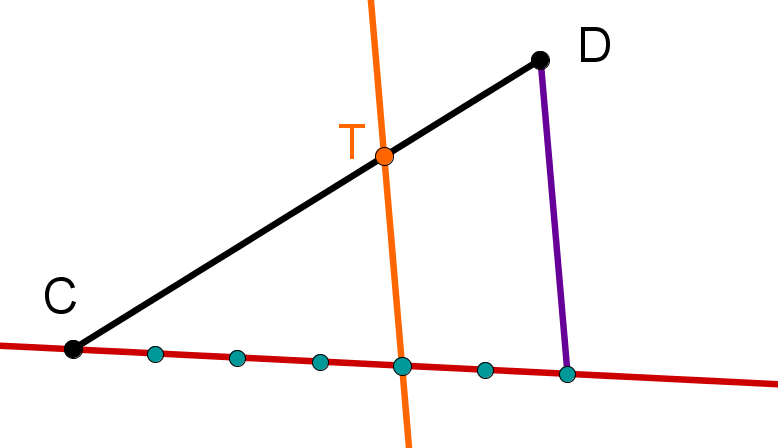
Die Länge der Teilstrecken und berechnet man mit der Formel: und
a=4, b=2 und
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
