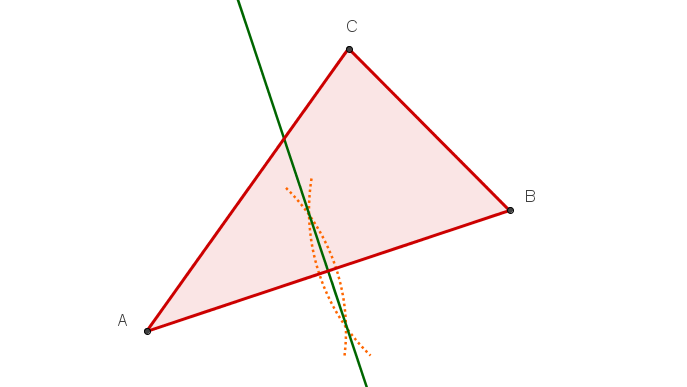
Zeichne ein beliebiges Dreieck (wie im Bild rechts).
Konstruiere dann nacheinander folgende Linien:
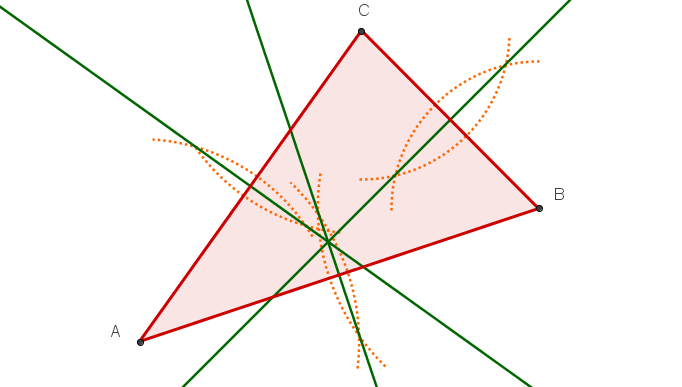
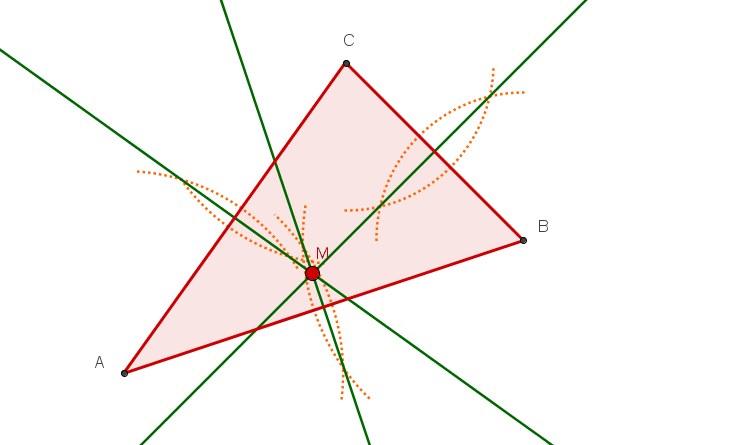
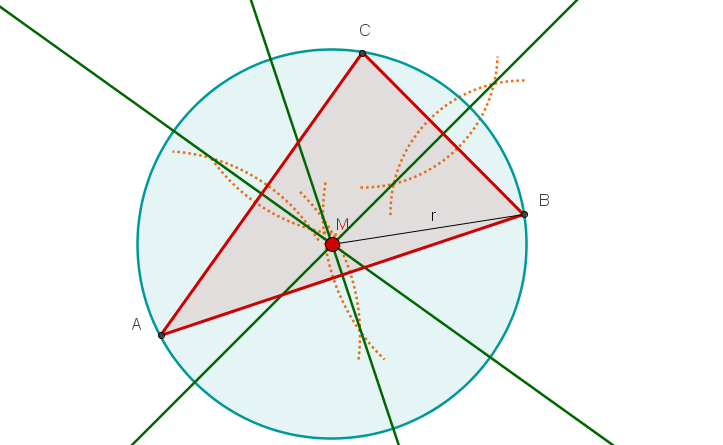
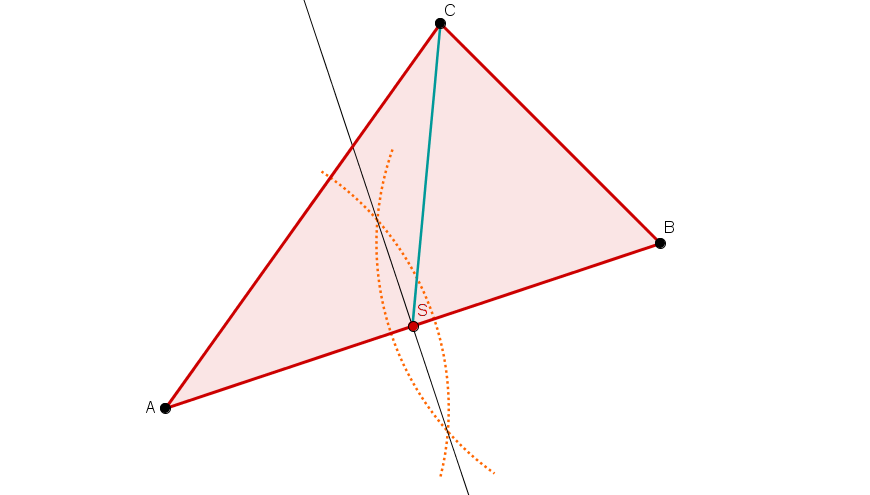
Alle drei Mittelsenkrechten und den Umkreis.
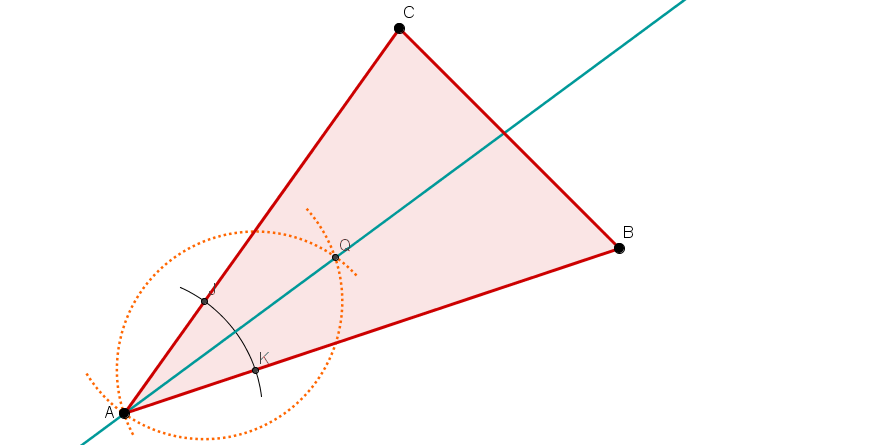
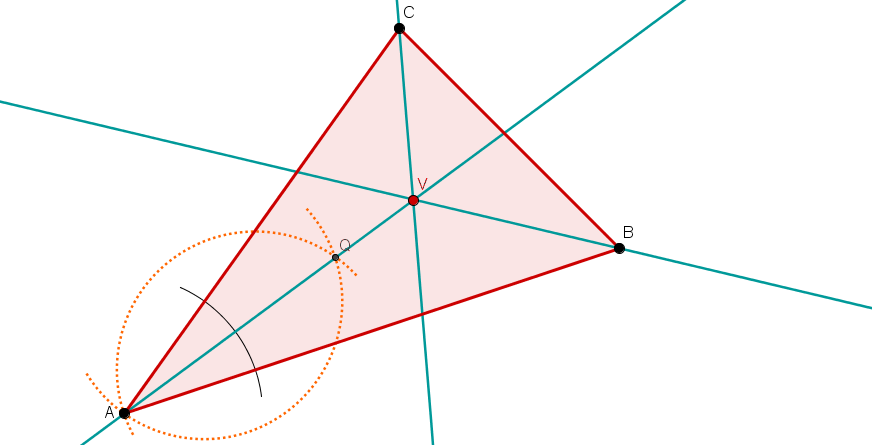
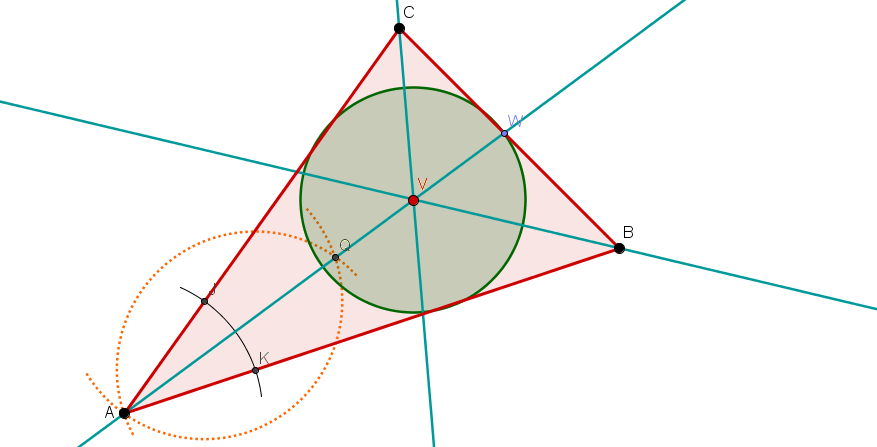
Alle drei Winkelhalbierenden und den Inkreis
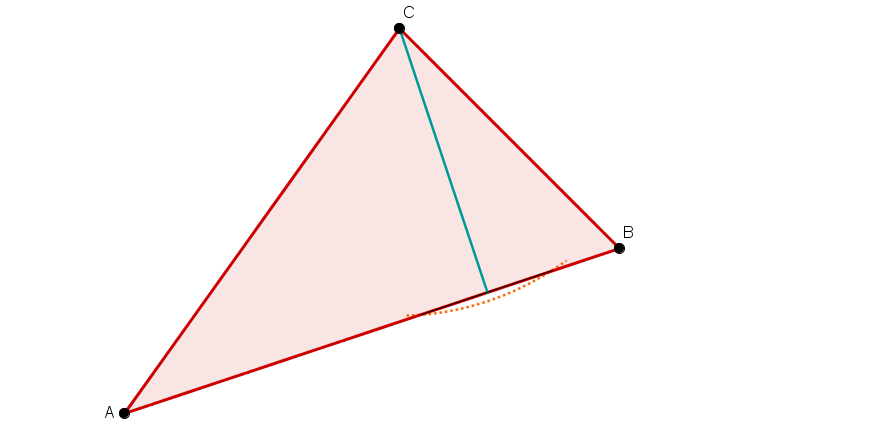
Alle drei Höhen.
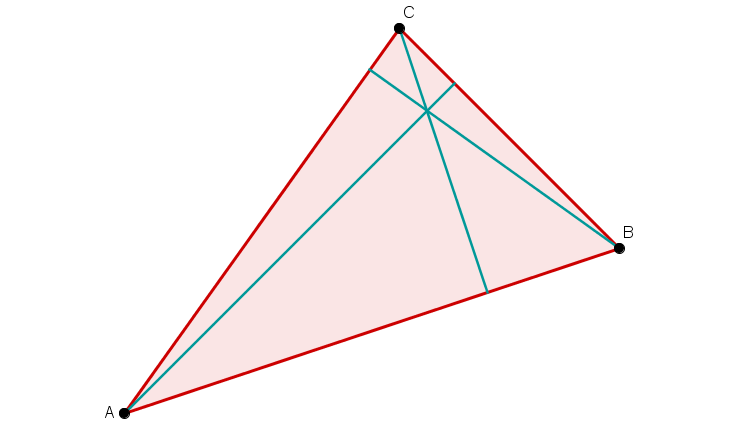
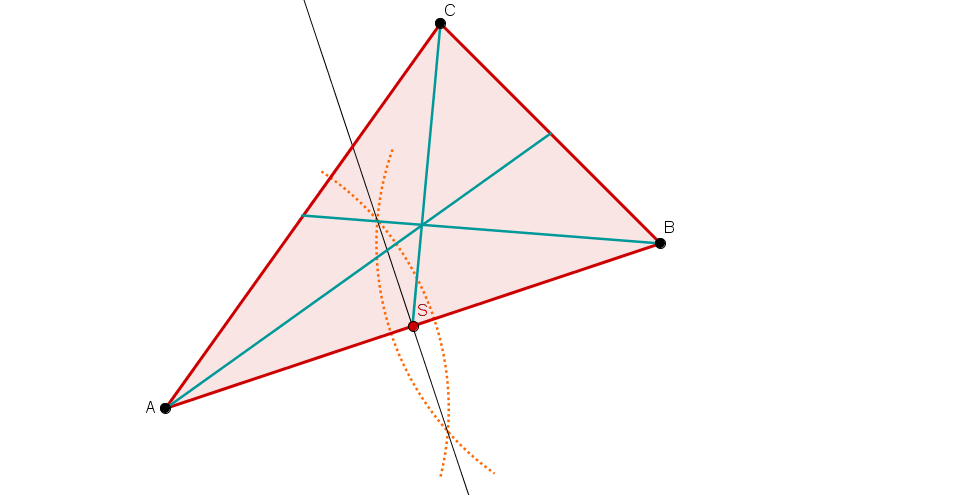
Alle drei Seitenhalbierenden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?