Weitere Anwendungsaufgaben zum Volumen

Wie gut kennst du dich mit Volumen aus? Teste dein Wissen mit diesen Anwendungsaufgaben!

1
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Die rechteckige Grundfläche eines Ölbehälters hat die Maße a=60cm und b=40cm.
Der Behälter ist mit V=140 Liter Öl gefüllt.
Welche Höhe h hat der Ölspiegel in ganzen cm?
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen und Massenberechnung
$V$ $=$ $140 l$
↓
Volumen in $d m^{3}$ umrechnen
$V$ $=$ $140 d m^{3}$
↓
$d m^{3}$ in $c m^{3}$ umrechnen
$V$ $=$ $140000 c m^{3}$
$V$ $=$ $c \cdot b \cdot h$ $: (a \cdot b)$
$h$ $=$ $\frac{V}{a \cdot b}$
↓
a, b und V einsetzen
$h$ $=$ $\frac{140 000 c m^{3}}{60 c m \cdot 40 c m}$
↓
multiplizieren und dividieren
$h$ $=$ $58, 3 c m$
↓
auf eine ganze Stelle runden
$h$ $\approx$ $58 c m$
2
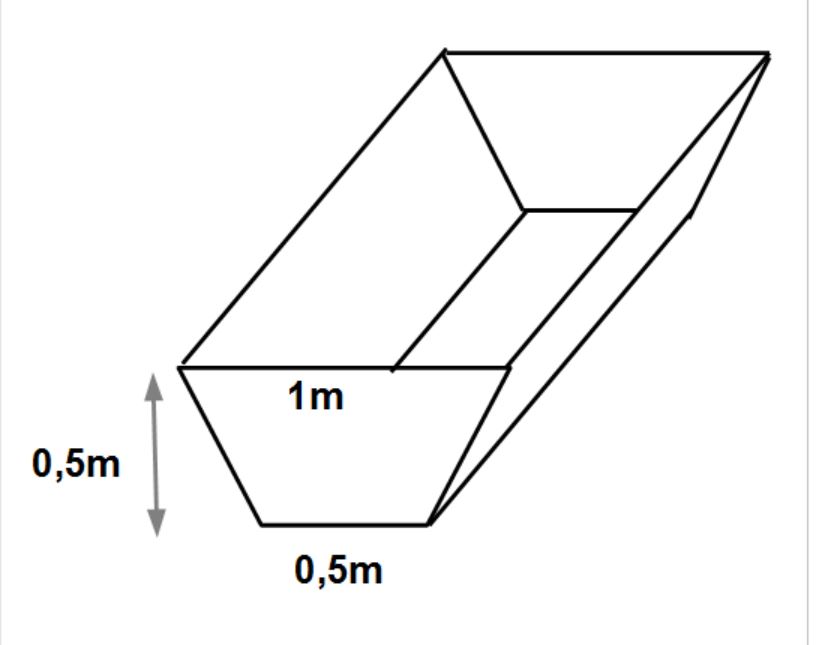
Von einem Wassertrog für Schweine ist bekannt, dass er $0,5 m$ hoch ist und die beiden parallelen Seiten an den trapezförmigen Flächen $0,5 m$ und $1,0 m$ lang sind.
1. Berechne, wie lang der Trog ist, wenn bekannt ist, dass insgesammt $750 l$ Wasser darin Platz finden.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prismavolumen
  Tipp: Überlege dir zuerst, welcher Körper hier vorliegt und welche Grundfläche er hat!
  $V = G \cdot h$
  Berechne zunächst die Grundfläche.
  Die Formeln findest du im Kapitel zum Trapez.
  $G = A_{T r a p e z} = \frac{a + c}{2} \cdot h$
  Notiere dir, welche Angaben du bereits gegeben hast.
  $a = 1 m$
  $c = 0,5 m$
  $h = 0,5 m$
  Setze in die Formel ein, um die Grundfläche zu berechnen.
  $A_{T r a p e z} = \frac{1 m + 0,5 m}{2} \cdot 0,5 m = 0,375 m^{2}$
  $V = 750 l$
  Rechne das Volumen in die Einheit $m^{3}$ um:
  $1 m^{3} = 1000 {dm}^{3} = 1000 l$
  Also musst du durch 1000 dividieren.
  $V = 750 l = 750 : 1000 m^{3}$
  $= 0,75 m^{3}$
  Forme die Volumenformel nach h um.
  $h = \frac{V}{G}$
  Setze G und V ein.
  $h = \frac{0,75 m^{3}}{0,375 m^{2}} = 2 m$
  Der Trog ist $2 m$ lang.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Das Wasser aus dem Trog reicht für 20 Schweine.
  Wie hoch müsste der Trog sein, wenn alle anderen Abmessungen gleich bleiben und er ausreichend Wasser für 35 Schweine beinhalten soll?
  Runde das Endergebnis auf zwei Nachkommastellen und gib es in der Einheit $m$ an!
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung
  $20 Schweine \hat{=} 750 l$
  $35 Schweine \hat{=} x l$
  Berechne zunächst die neue Wassermenge, zum Beispiel mithilfe des Dreisatzes.
  $20 Schweine \hat{=} 750 l | : 20$
  $1 Schwein \hat{=} 37,5 l | \cdot 35$
  $35 Schweine \hat{=} 1312,5 l$
  Rechne in $m^{3}$ um:
  $1 m^{3} = 1000 l$
  Du musst also durch 1000 dividieren.
  $V = 1312,5 l = 1312,5 : 1000 m^{3} = 1,3125 m^{3} \approx 1,31 m^{3}$
  Prismavolumen
  $V$ $=$ $G \cdot h$
  ↓
  Stelle nach G um
  $G$ $=$ $\frac{V}{h}$
  ↓
  Setze die bekannten Werte ein
  $h$ $=$ $2 m (a u s T e i l a u f g a b e a)$
  ↓
  Stelle die Formel für die Fläche des Trapez nach h um
  $V$ $=$ $1,31 m^{3}$
  $G$ $=$ $\frac{1,31 m^{3}}{2 m}$
  $=$ $0,66 m^{2}$
  $A_{T r a p e z} = \frac{a + c}{2} \cdot h$
  $h = \frac{2 \cdot A_{T r a p e z}}{a + c}$
  Setze die bekannten Werte ein
  $h = \frac{2 \cdot 0,66 m^{2}}{1,0 m + 0,5 m} = 0,88 m$
  Der neue Trog müsste 0,88 m tief sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Wie viel Brause passt in diese Riesenflasche?
An einem Hochhaus in der Chemnitzer Innenstadt wurde dieses Werbeplakat befestigt:
Diese "Riesenflasche" ist natürlich viel höher, breiter und tiefer als eine im Laden erhältliche Brauseflasche. Die Flasche aus dem Laden hat eine Höhe von ungefähr 23 cm und ein Volumen von 0,33 l.
Wie hoch unsere Riesenflasche ist, kannst du aus dem Bild ungefähr abschätzen. Vielleicht schaffst du das auch ohne Hilfe.
Berechne nun das ungefähre Volumen an Fassbrause in unserer Riesenflasche. Beachte dabei, dass es sich sowohl bei der Riesenflasche, als auch bei der kleinen Fasche um Körper handelt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung
Wir wandeln zunächst die Höhe der kleinen Flasche in die Einheit Meter um, damit beide Höhen die gleiche Einheit haben.
$23 c m = 0,23 m$
Nun dividieren wir die Höhe der Riesenflasche durch die Höhe der kleinen Flasche.
$24 m : 0,23 m = 104$
Da wir die Größe nur durch Abschätzen ermittelt haben, können wir unser Zwischenergebnis auch noch stärker runden. Unsere Riesenflasche ist also ungefähr 100 mal so hoch, wie eine kleine Brauseflasche.
Da es sich um Körper handelt, ist das Volumen der Riesnflasche demzufolge
$100 \cdot 100 \cdot 100 = 1000000$
mal so groß, wie das Volumen der kleinen Flasche.
Die Riesenflasche enthält also
$1000000 \cdot 0,33 l = 330000 l$
Da wir die Maße teilweise abgeschätzt haben und wir außerdem in der Zwischenrechnung bereits stark gerundet haben, runden wir das Endergebnis ebenfalls nochmals.
Antwortsatz:
Die Riesenflasche würde ungefähr 330.000 Liter Brause enthalten.
4
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Die Erde kann in sehr guter Näherung als kugelförmig, mit dem Radius $R = 6370 k m$ angenommen werden. $71 %$ der Erdoberfläche sind von Meeren bedeckt, die durchschnittlich eine Tiefe von etwa $3,7 k m$ aufweisen.
Auf dem Festland der Antarktis lagern ca. $21$ Millionen Kubikkilometer Süßwasser als Eis und Schnee.
1. Berechne das Salzwasservorkommen der Erde in Kubikkilometer! (Achten Sie auf sinnvolles Runden!)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel
  Berechnung der gesamten Oberfläche der Meere:
  $A = 0,71 \cdot 4 \cdot R^{2} π = 0,71 \cdot 4 \cdot 6370^{2} {km}^{2} \cdot π \approx 362 \cdot 10^{6} {km}^{2}$
  Berechnung des Volumens:
  $V \approx A \cdot 3,7 k m = 362 \cdot 10^{6} k m^{2} \cdot 3,7 k m \approx 1,3 \cdot 10^{9} k m^{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie viele Meter müsste der Wasserspiegel der Meere steigen, wenn die gesamten Eis- und Schneemassen des Festlandes schmelzen würden? Für deine Berechnung soll die Landfläche der Erde unverändert bleiben (und sich nicht durch Überschwemmungen verkleinern).
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel
  Berechnung des Wasserspiegelanstiegs:
  $\begin{array}{l} 21 \cdot 10^{6} k m^{3} = A \cdot x \\ \Rightarrow x = \frac{21 \cdot 10^{6} k m^{3}}{362 \cdot 10^{6} k m^{2}} \approx 0,058 k m = 58 m \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$V$	$=$	$140 l$
	↓	Volumen in $d m^{3}$ umrechnen
$V$	$=$	$140 d m^{3}$
	↓	$d m^{3}$ in $c m^{3}$ umrechnen
$V$	$=$	$140000 c m^{3}$

$V$	$=$	$c \cdot b \cdot h$	$: (a \cdot b)$
$h$	$=$	$\frac{V}{a \cdot b}$
	↓	a, b und V einsetzen
$h$	$=$	$\frac{140 000 c m^{3}}{60 c m \cdot 40 c m}$
	↓	multiplizieren und dividieren
$h$	$=$	$58, 3 c m$
	↓	auf eine ganze Stelle runden
$h$	$\approx$	$58 c m$

$V$	$=$	$G \cdot h$
	↓	Stelle nach G um
$G$	$=$	$\frac{V}{h}$
	↓	Setze die bekannten Werte ein
$h$	$=$	$2 m (a u s T e i l a u f g a b e a)$
	↓	Stelle die Formel für die Fläche des Trapez nach h um
$V$	$=$	$1,31 m^{3}$
$G$	$=$	$\frac{1,31 m^{3}}{2 m}$
	$=$	$0,66 m^{2}$

Weitere Anwendungsaufgaben zum Volumen

Hast du eine Frage oder Feedback?

Prismavolumen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?