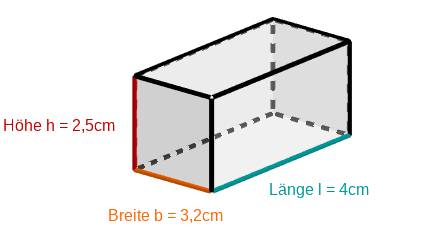
Die nicht maßstabsgetreue Skizze zeigt einen Quader und dessen Abmessungen. Berechne die Oberfläche des Quaders.
cm²
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Die nicht maßstabsgetreue Skizze zeigt einen Quader und dessen Abmessungen. Berechne die Oberfläche des Quaders.
