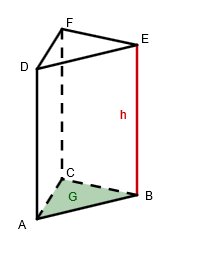
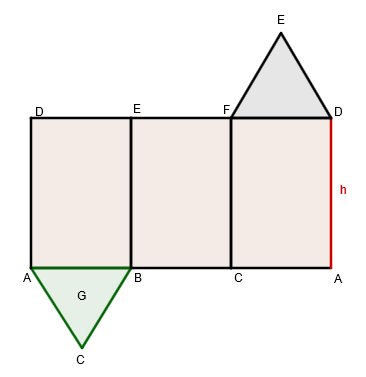
Ein Prisma ist ein dreidimensionaler Körper, der
auf der einen Seite ein n-Eck als Grundfläche,
von dort aus parallele und gleich lange Kanten,
und auf der gegenüberliegenden Seite ein zur Grundfläche kongruentes n-Eck als Deckfläche
hat.
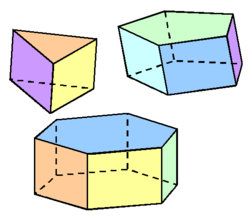
Beispiele versch. Prismen: dreiseitiges, fünfseitiges und sechsseitiges Prisma
Bei der Bezeichnung der Prismen wie dreiseitiges und fünfseitiges Prisma bezieht man sich auf die Anzahl der Seitenflächen.
Wenn die parallelen Kanten senkrecht auf der Grundfläche stehen, ist das Prisma ein gerades Prisma, andernfalls ein schiefes Prisma.
In der Schule werden oft nur gerade Prismen betrachtet.
Beispiele für Prismen in der realen Welt
Manche Gegenstände habe ungefähr die Form eines Prismas:
Diese Geschenkschachtel hat ungefähr die Form eines Primas, mit einem regulären Sechseck als Grundfläche.

Wenn ein Marmeladenglas nicht rund ist, sondern eckig - so wie im Bild das mittlere Glas - dann liegt ihm als Grundform nicht ein Zylinder, sondern ein Prisma zugrunde.

Mit der Vorderfront als "Grundfläche" ist solch ein Gewächshaus annähernd ein Prisma.

In der Physik werden Prismen aus Glas oder Kunststoff verwendet, um weißes Licht in Regenbogenfarben zu zerlegen.
Mit einem dreiseitigen Prisma aus Glas kann man eindrucksvoll die Lichtbrechung demonstrieren.
Prisma durch Parallelverschiebung eines Vielecks
Man kann sich ein Prisma als ein dreidimensionales Objekt vorstellen, das durch eine Parallelverschiebung eines n-Ecks entsteht. Die Verschieberichtung darf dabei nicht innerhalb der Ebene des n-Ecks liegen (3. Dimension notwendig).
Beispiel: Alle Eckpunkte des unteren Dreiecks (siehe Bild) werden entlang paralleler Geraden nach oben verschoben, sodass oben das gleiche Dreieck noch einmal erscheint.
Unteres Dreieck, oberes Dreieck und alle Punkte dazwischen bilden dann zusammen das Prisma.

Beispiel eines dreiseitigen Prismas, das durch Parallelverschiebung eines Dreiecks entsteht.
Bezeichnungen beim Prisma
Grundfläche eines Prismas
Als Grundfläche des Prismas bezeichnet man eines der beiden kongruenten Vielecke, die durch die parallelen Kanten verbunden sind.
(Das gegenüberliegende kongruente Vieleck nennt man dann Deckfläche. Welches der beiden Vielecke man als Grundfläche und welches als Deckfläche auffasst, ist in der Regel egal.)
An diesem Beispiel kann man erkennen, dass die "Grundfläche" trotz ihrer Bezeichnung nicht unbedingt unten sein muss. Ein Prisma kann auch auf einer der Seitenflächen liegen.
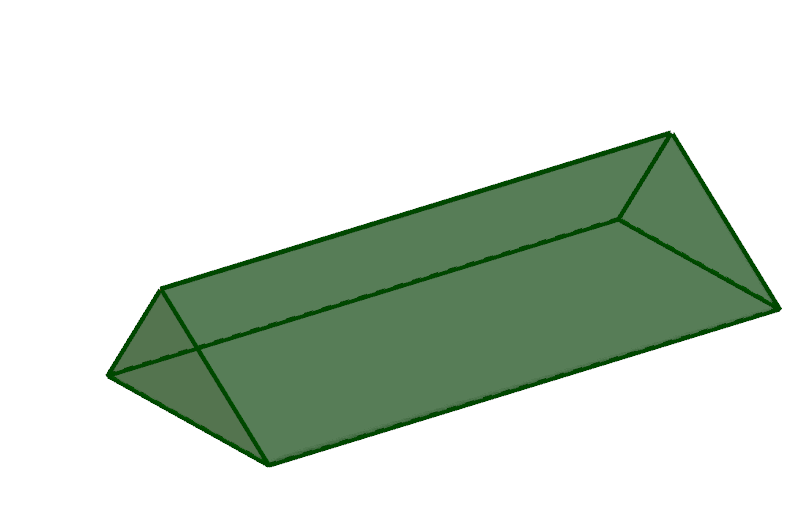
Liegendes Prisma mit dreieckiger Grundfläche
Höhe eines Prismas
Die Höhe eines Prismas ist der Abstand zwischen der Ebene, in der die Grundfläche des Prismas liegt, zu der Ebene, in der die (der Grundfläche gegenüber liegende) Deckfläche liegt.
Höhe bei einem geraden Prisma
Bei einem geraden Prisma ist die Höhe gleich der Länge der parallelen Kanten und
wenn das Prisma auf der Grundfläche steht, ist das auch wirklich die "Höhe" des Prismas im umgangssprachlichen Sinn.

Bei einem stehenden geraden Prisma ist die Höhe des Prismas tatsächlich die "Höhe" des Prismas.
Wenn das Prisma auf einer der Seitenflächen liegt, ist die "Höhe des Prismas" das, was man normalerweise wahrscheinlich eher "Länge des Prismas" nennen würde.
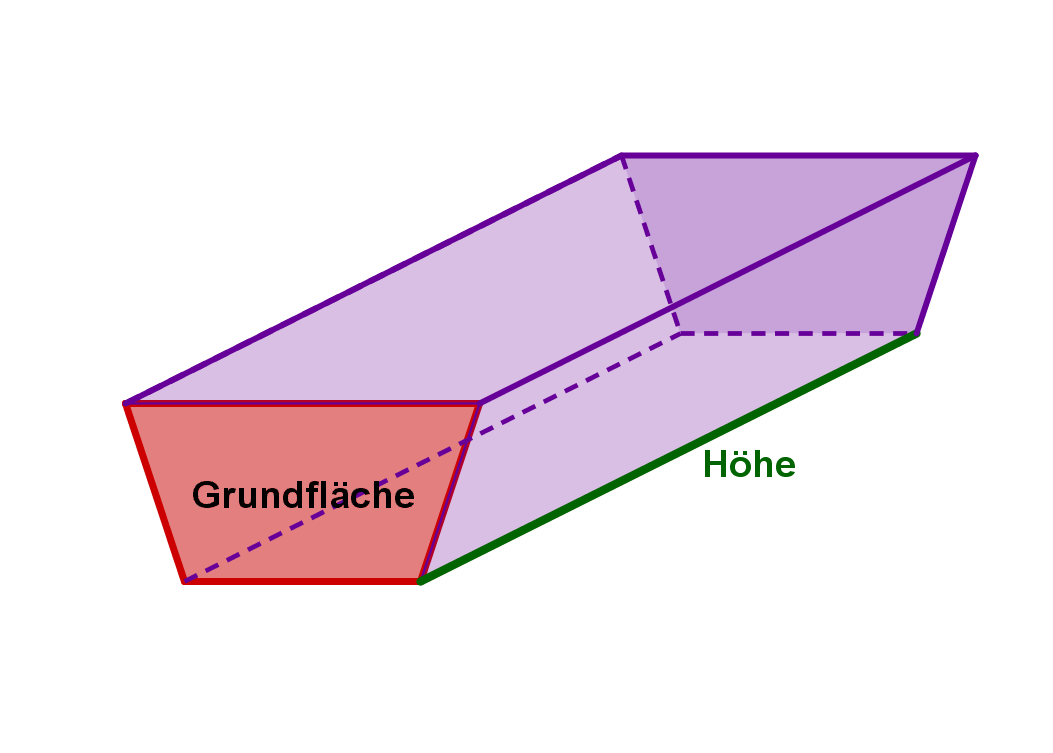
Bei einem liegenden geraden Prisma erkennt man die Höhe nur dann als eine "Höhe", wenn man sich das Prisma auf die Grundfläche aufgestellt denkt.
Höhe eines schiefen Prismas
Bei einem schiefen Prisma muss die Höhe trotzdem als senkrechter Abstand gemessen werden - das heißt, die Höhe liegt "außerhalb" des Prismas.
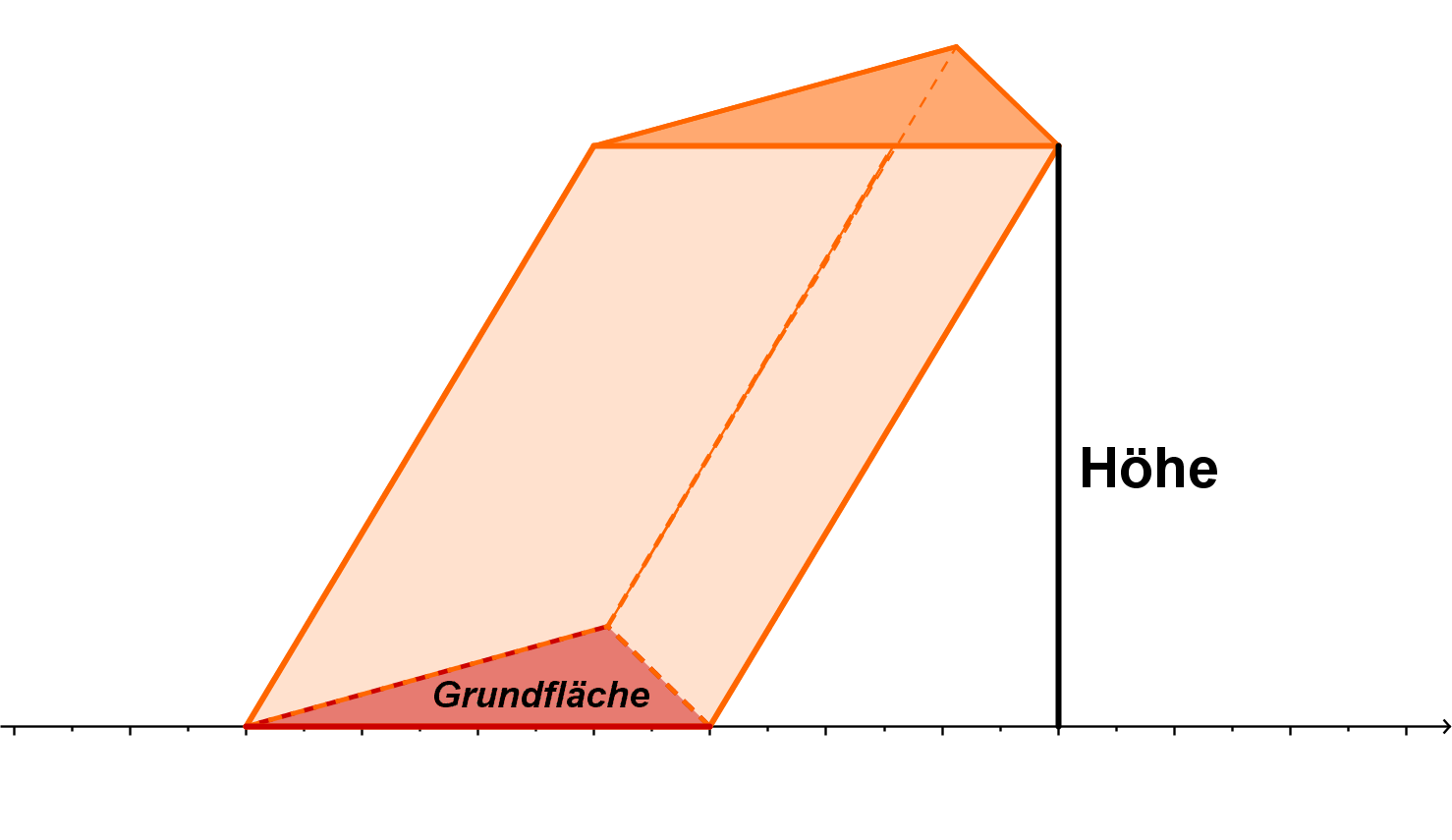
Bei solch einem auf der Grundfläche stehenden schiefen Prisma misst man die Höhe einfach von der Deckfläche aus senkrecht zum Boden herunter.
Wichtige Formeln zum Prisma
Bemerkung: Bei den Abbildungen zu den Formeln ist hier immer nur ein dreiseitiges Prisma gezeichnet, das heißt, ein Prisma, das ein Dreieck als Grund- und als Deckfläche besitzt. Natürlich kann ein Prisma aber auch mehr Seiten haben!
Volumen
Mantelfläche
n bezeichnet die Anzahl der Seitenflächen
bezeichnen die Seitenflächen des Prismas
Hat die Grundfläche einen Umfang , gilt für die Mantelfläche .
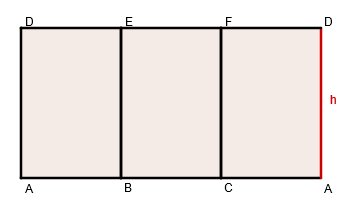
Oberflächeninhalt
Video zum Thema Volumen und Oberfäche des Prismas
Laden
Gerades und schiefes Prisma
Wenn die parallelen Begrenzungslinien, die die Grundfläche und die Deckfläche miteinander verbinden,
senkrecht auf der Grundfläche
stehen, hat man ein gerades Prisma.

Beispiel eines geraden Prismas mit achteckiger Grundfläche
Wenn die parallelen Begrenzungslinien aber
nicht senkrecht auf der Grundfläche
stehen, ergibt sich ein schiefes Prisma.
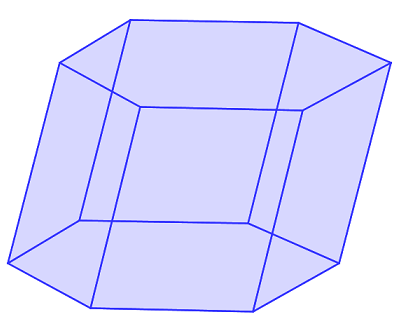
Beispiel eines schiefen Prismas mit sechseckiger Grundfläche
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Prisma
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: