Bei einer Drehung verschiebt man einen Punkt auf einer Kreislinie um einen beliebigen Drehwinkel . Das heißt insbesondere: Bei der Drehung eines Punktes um den Punkt ändert sich der Abstand von zu nicht!
Abbildungsgleichung der Drehung um den Ursprung
Bei einer Drehung um den Ursprung (Drehzentrum) mit dem Winkel wird der Punkt auf den Punkt abgebildet.
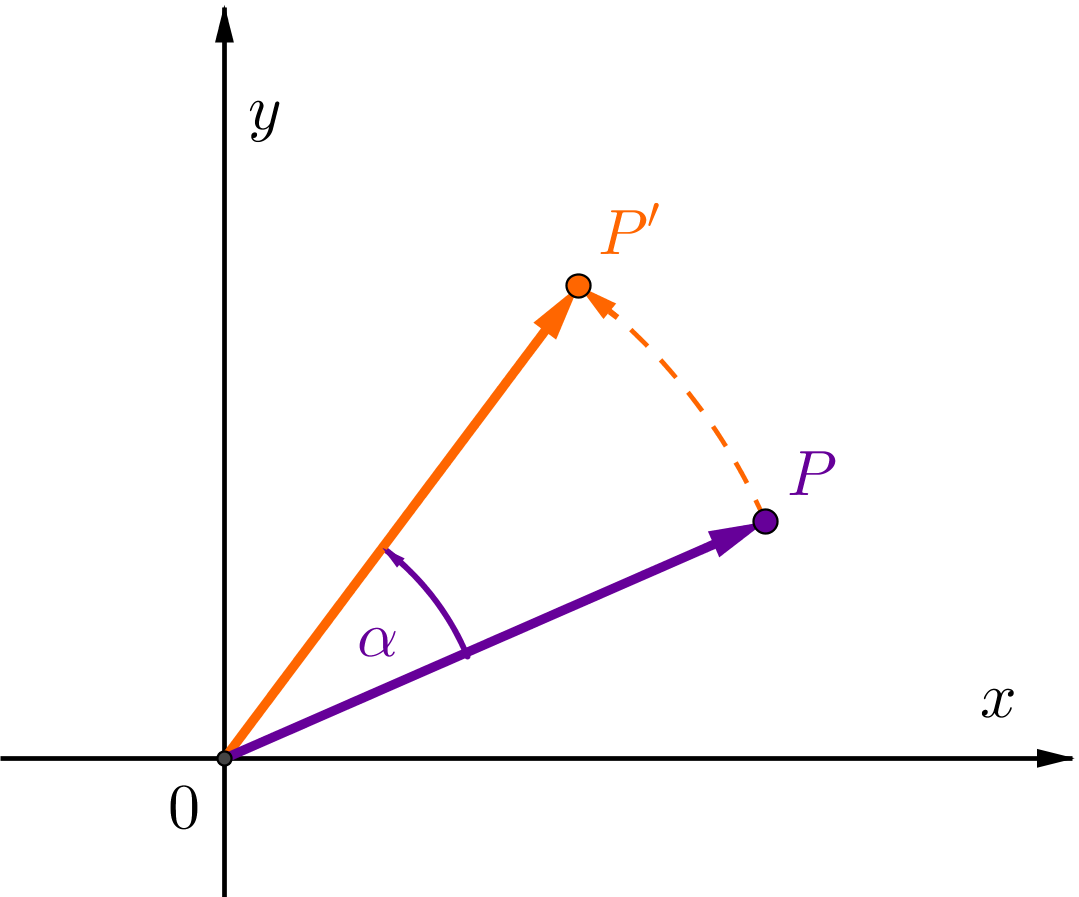
Koordinatenform:
Matrixform:
Beispiel:
Drehe den Punkt um den Ursprung mit dem Drehwinkel !
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
