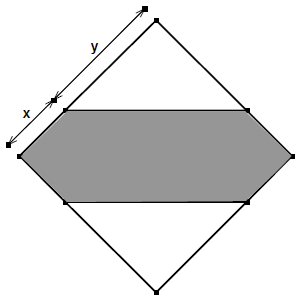
In das Quadrat ist ein grau gefärbter "Doppelpfeil" eingezeichnet.
Gib den Flächeninhalt des Doppelpfeils in Abhängigkeit von und an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
In das Quadrat ist ein grau gefärbter "Doppelpfeil" eingezeichnet.
Gib den Flächeninhalt des Doppelpfeils in Abhängigkeit von und an.
