Kombinations- und Rätselaufgaben mit natürlichen Zahlen
Wie gut kennst du dich mit natürlichen Zahlen aus? Lerne spielerisch das Rechnen mit natürlichen Zahlen mit diesen Kombinations- und Rätselaufgaben.
- 1
Stelle mit vier Vieren und den dir bekannten Rechenzeichen die Zahlen von 0 bis 9 dar.
- 2
In einer Zielscheibe mit konzentrischen Ringen erhält man für den innersten Ring 87 Punkte und für die nach außen darauffolgenden Ringe 73, 59 und 31 Punkte. Bei dieser Zielscheibe wurden mit dem Pfeil genau 301 Punkte erzielt. Finde heraus, wie oft in welche Ringe getroffen wurde.
- 3
Bestimme alle zweistelligen natürlichen Zahlen x, welche zugleich folgende Bedingungen erfüllen:
x ist größer als 60,
x hat genau vier Teiler,
x ist ungerade,
vertauscht man bei x die beiden Ziffern, so erhält man eine Primzahl.
Begründe, warum du die gesuchten Zahlen schneller findest, wenn du dich nicht streng an die vorgegebene Reihenfolge der Bedingungen hältst.
Begründe, warum die vierte Bedingung die 60er und 80er Zahlen ausschließt.
In welcher Reihenfolge führen die Bedingungen deiner Meinung nach am schnellsten zur Lösung?
- 4
Untersuche die Teilbarkeit folgender Summen:
a) Summe drei aufeinanderfolgender Zahlen.
b) Summe fünf aufeinanderfolgender Zahlen.
c) Summe vier aufeinanderfolgender Zahlen.
- 5
Die Summe der geraden natürlichen Zahlen kleiner als wird mit bezeichnet.
Was ist die Summe der ungeraden natürlichen Zahlen unterhalb von in Abhängigkeit von ?
- 6
Schreibe drei natürliche Zahlen auf, von denen die zweite um und die dritte um größer ist als die erste, z. B. .
Dividiere jede der drei aufgeschriebenen Zahlen durch und notiere die Reste.
Welche Aussage kann man in allen Beispielen über die auftretenden Reste machen?
Begründe: Wenn von drei natürlichen Zahlen die zweite um und die dritte um größer ist als die erste, dann ist eine der Zahlen durch teilbar.
- 7
Stelle mit den Zahlen und , verschiedene Terme auf und berechne sie.
Bei mindestens drei Termen soll das Ergebnis mindestens und höchstens sein.
Bei mindestens drei Termen soll das Ergebnis mindestens und höchstens sein.
- 8
Iris betrachtet Zahlenschlangen von besonderer Form: Der Kopf besteht aus einer zweistelligen, der Körper aus einer dreistelligen Zahl. Weder beim Kopf noch beim Körper ist die erste Ziffer Null.
Beispiele: oder
Wie viele Schlangen dieser Form gibt es?
ZahlenschlangenSchlangen, deren ,,Kopfzahlen” und ,,Körperzahlen” jeweils dieselbe Quersumme haben, gehören zur selben Familie. So sind z. B. die Schlangen und in derselben Familie. Wie viele Schlangen gehören ebenfalls zu dieser Familie?
SchlangenIris findet eine Familie, die aus genau sechs Schlangen besteht. Kannst du auch eine solche Familie angeben? Schreibe deine Familie auf!
- 9
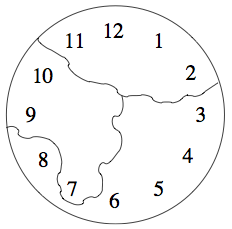
Auf einer Uhr finden sich die zwölf Zahlen von Eins bis Zwölf.
Die Uhr zerbricht beim Herunterfallen in drei Stücke. Kann es sein, dass die Summe der Zahlen auf jedem Teil gleich ist?
Lässt sich aus den Zahlen in der Tabelle einen Rechenausdruck bilden, der Null ergibt?
- 10
Es stehen die Ziffern jeweils einmal zur Verfügung. Bilde Rechenausdrücke mit dem jeweils größten und kleinsten Wert unter Verwendung...
(Beachte: Eine ganze, nicht einstellige Zahl darf nicht mit der Ziffer beginnen.)
... aller Ziffern und eines Pluszeichens.
... aller Ziffern und eines Minuszeichens.
... aller Ziffern, eines Plus- und eines Minuszeichens.
- 11
Bei einer Anordnung von Würfeln addiert man alle sichtbaren Augenzahlen, die nicht durch den Tisch oder Nachbarwürfel verdeckt sind.
Es werden drei Spielwürfel übereinander zu einem Turm aufgebaut. Wie groß ist die Augensumme?
Wie muss man die Würfel in diesem Turm anordnen, damit die Augensumme maximal wird?
Wie groß ist die maximale Augensumme bei einem Turm mit vier, fünf und n Würfel?
Es werden drei, vier, fünf und n Würfel nebeneinander in eine Reihe gelegt.
Wie groß ist dann die maximale Augensumme?
Es werden acht Würfel zu einem quadratischen Rahmen gelegt. Wie groß ist die maximale Augensumme?
Es werden neun, sechzehn, und Würfel zu einem Quadrat gelegt. Wie groß ist die maximale Augensumme?
- 12
Löse die folgenden Aufgaben:
Nenne die größte vierstellige Zahl, die genau eine 9 enthält.
Nenne die größte vierstellige Zahl, die genau eine 8 enthält.
Nenne die größte vierstellige Zahl, die keine Ziffer zweimal enthält.
Nenne die kleinste vierstellige Zahl, die keine Ziffer zweimal enthält.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?