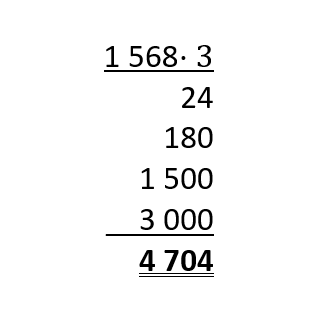Aufgaben zum schriftlichen Multiplizieren
Wie gut kennst du dich aus? Teste dein Wissen zum schriftlichen Multiplizieren mit diesen Übungsaufgaben!
- 1
Multipliziere die beiden Zahlen schriftlich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Mulitiplikation
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Es reicht, zu berechnen und am Ende eine Null hinzuzufügen. Denn:
Berechne also:
Füge nun an das Ergebnis eine Null an, indem du es mit 10 multiplizierst:
Das Ergebnis ist also .
Hast du eine Frage oder Feedback?
- 2
Berechne das Ergebnis der Multiplikation.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation
↓ Berechne zuerst des ersten Produkt
↓ Bei der Multiplikation mit 10 muss man lediglich eine 0 am Ende der Zahl hinzufügen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation
Im Produkt kommen 2 zweistellige Zahlen vor. Es ist einfacher, wenn wir möglichst keine Multiplikation mit zweistellige Zahlen, sondern nur Multiplikationen mit einstelligen Zahlen durchführen müssen. Da die Multiplikation natürlicher Zahlen assoziativ und kommutativ ist, können wir die Faktoren vertauschen und in beliebigen Reihenfolge multiplizieren.
Wir berechnen zuerst , da das Ergebnis 60 sich bei der Multiplikation ähnlich verhält wie einstellige Zahlen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation
Berechne das erste Produkt .
Zwischenrechnung:
Einerstelle: . Deshalb an der Einerstelle des Ergebnis schreiben und bei der Zehnerstelle notieren.
Zehnerstelle: rechnen und die notierte dazu addieren, also .
Das Produkt einer Zahl mit der ist immer die Zahl selbst.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation
Jedes Produkt ist , wenn einer der Faktoren ist.
Hast du eine Frage oder Feedback?
- 3
Multipliziere die beiden Zahlen schriftlich!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Beginne damit, die Rechnung aufzuschreiben und einen Strich darunter zu machen. Anschließend fängst du mit der Multiplikation an.
Berechne nun Schritt für Schritt die einzelnen Multiplikationen. In diesem Fall fängst du mit an.
Schreibe nun für die nächste Multiplikation eine 0 unter die 1 der 21.
Anschließend kannst du die nächste Multiplikation durchführen.
Für die letzte Multiplikation schreibst du zwei Mal die 0 unter die 50 und rechnest anschließend .
Ziehe nun erneut einen Strich unter die 700 und berechne die Addition der Zahlen 21, 150 und 700 mithilfe der schriftlichen Addition.
Die Lösung ist: .
Hast du eine Frage oder Feedback?
Merke: Du kannst die beiden Faktoren nach Belieben vertauschen, falls es dir dann leichter fällt zu rechnen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Multipliziere die einzelnen Ziffern der linken Zahl mit der 3.
Addiere anschließend die Zahlen schriftlich um auf die Lösung zu kommen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Beginne, indem du die grüne 1 mit der 111 multiplizierst.
Die Farben lassen erkennen, welche Rechenschritte mit welcher Ziffer der rechten Zahl zusammengehören.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Beginne mit der grünen 1 und berechne die einzelnen Multiplikationen mit der 356.
Die grünen Rechenschritte wurden mit der 1 gemacht, die roten mit der 7.
Insgesamt erhältst du die Lösung
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Beginne mit der grünen 5 und berechne die einzelnen Multiplikationen mit der 72.
Die grünen Rechenschritte wurden mit der 5 gemacht, die roten mit der 6.
Insgesamt erhältst du die Lösung
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Beginne mit der grünen 2 und berechne die einzelnen Multiplikationen mit der 386.
Die grünen Rechenschritte wurden mit der 2 gemacht, die roten mit der 8.
Insgesamt erhältst du die Lösung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Beginne mit der grünen 7 und berechne die einzelnen Multiplikationen mit der 5 268.
Die grünen Rechenschritte wurden mit der 7 gemacht, die roten mit der 6.
Insgesamt erhältst du die Lösung .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die türkisen Zahlen entstanden bei der Multiplikation mit der Hunderter-Stelle (in diesem Fall ).
Die grünen Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die roten Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die türkisen Zahlen entstanden bei der Multiplikation mit der Hunderter-Stelle (in diesem Fall ).
Die grünen Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die roten Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .
Hast du eine Frage oder Feedback?
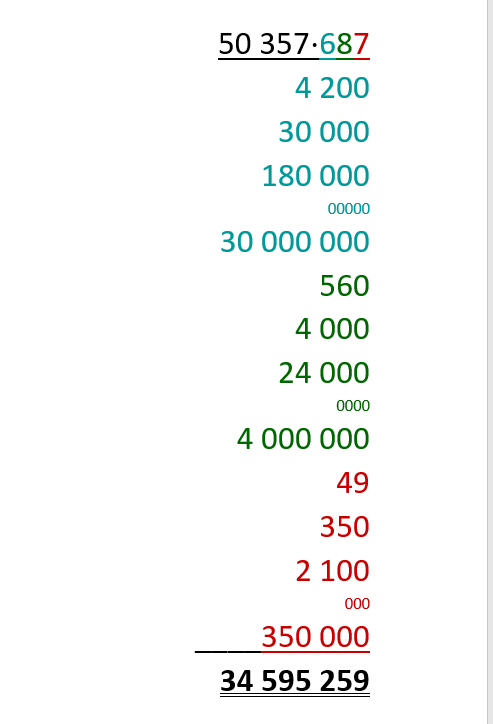
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die türkisen Zahlen entstanden bei der Multiplikation mit der Hunderter-Stelle (in diesem Fall ).
Die grünen Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die roten Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .
Hast du eine Frage oder Feedback?
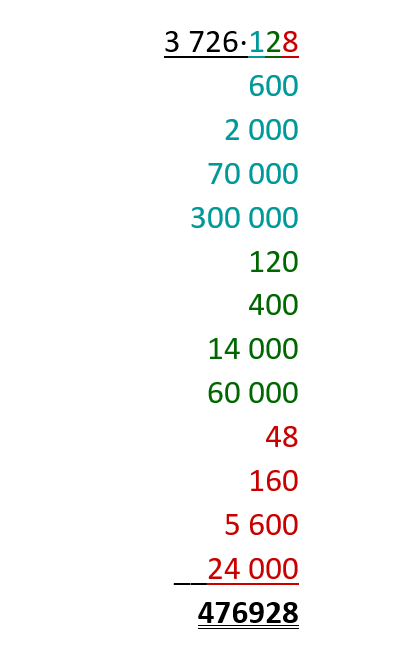
Für diese Aufgabe benötigst Du folgendes Grundwissen: Anleitung zum schriftlichen Multiplizieren
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die orangen Zahlen entstanden bei der Multiplikation mit der Tausender-Stelle (in diesem Fall ).
Die türkisen Zahlen entstanden bei der Multiplikation mit der Hunderter-Stelle (in diesem Fall ).
Die grünen Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die roten Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .
Hast du eine Frage oder Feedback?
- 4
Tim geht im Moment in die 5.Klasse. Er hat jeden Tag 5 Stunden Unterricht. In diesem Schuljahr gibt es 196 Schultage. Wie viele Stunden verbringt er also dieses Schuljahr ingesamt in der Schule?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Es gibt Schultage mit jeweils Schulstunden, du musst also die mit multiplizieren
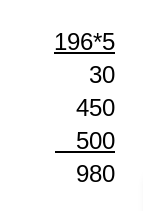
Als Lösung erhältst du .
Nutze die Schritt für Schritt Anleitung zum schriftlichen Multiplizieren und vergleiche die Teilschritte mit der Lösung!
- 5
Herr Müller muss für einen Ausflug der 5. Klassen Geld einsammeln. Jeder Schüler muss ihm für die Fahrkarte und die Eintrittskarte 12€ zahlen. In allen 5. Klassen sind 127 Schüler. Wie viel Geld muss Herr Müller am Ende haben?
: Schreibe in das Lösungsfeld nur die Zahl ohne € Zeichen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: schriftliche Multiplikation
Es gibt insgesamt Schüler, die je € bezahlen müssen, du musst also und miteinander multiplizieren.
Nutze die Schritt für Schritt Anleitung zum schriftlichen Multiplizieren und vergleiche die Teilschritte mit der Lösung!
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die roten Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die blauen Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .

- 6
In einer Fabrik werden täglich 1325 Fußbälle hergestellt. Da gerade viele Leute Fußbälle kaufen, wird die Produktion auch am Wochenende nicht gestoppt. Es werden also die ganze Woche über Fußbälle angefertigt. Wie viele Fußbälle werden dann in zwei Wochen produziert?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Eine Woche hat Tage, zwei Wochen haben dann also Tage. Du musst also mit multiplizieren.
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die roten Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die blauen Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .

Nutze die Schritt für Schritt Anleitung zum schriftlichen Multiplizieren und vergleiche die Teilschritte mit der Lösung!
- 7
Jeden Monat kommen am Hamburger Hafen 235.145 Schiffscontainer an. Wie viele Container werden dann jährlich eingeführt?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schriftliche Multiplikation
Ein Jahr hat Monate. Das heißt, du musst die monatliche Anzahl an Schiffscontainern mit multiplizieren
Die einzelnen Rechenschritte sind farblich markiert, damit du sie besser zuordnen kannst.
Die roten Zahlen entstanden bei der Multiplikation mit der Zehner-Stelle (in diesem Fall ).
Die blauen Zahlen entstanden bei der Multiplikation mit der Einer-Stelle (in diesem Fall ).
Als Lösung erhältst du .

Nutze die Schritt für Schritt Anleitung zum schriftlichen Multiplizieren und vergleiche die Teilschritte mit der Lösung!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?