Das Sieb des Eratosthenes ist ein Verfahren, um systematisch alle Primzahlen aus einer Liste von Zahlen zu bestimmen. Diese Liste beginnt mit der Zahl und enthält alle darauffolgenden natürlichen Zahlen bis zu einer festgelegten größten Zahl. Eins wird nicht betrachtet, weil sie direkt als Primzahl ausgeschlossen werden kann. Man könnte auch sagen, dass mit diesem Verfahren alle Primzahlen der Liste herausgesiebt werden.
Das Verfahren
Um nun alle Primzahlen einer gegebenen Liste zu bestimmen, werden folgende Schritte durchlaufen:
Zunächst wählt man die kleinste Zahl der Liste aus und umkreist sie. Bei der ersten Bearbeitung der Liste wird dabei die Zahl ausgewählt. Alle Vielfachen dieser Zahl werden dann in der Liste gestrichen. Für die Zahl bedeutet dies, dass , , ,… gestrichen werden.
Dann wird die nächste noch nicht durchgestrichene Zahl der Liste ausgewählt und umkreist. Dies ist nun die Zahl .
Für die nun ausgewählte Zahl werden wie im ersten Verfahrensschritt ihre Vielfachen aus der Liste gestrichen.
Die beschriebene Verfahrensweise wird so lange wiederholt, bis keine zu streichenden Zahlen mehr übrig sind.
Das Verfahren ist dann beendet und die umkreisten Zahlen sind alle Primzahlen der Liste.
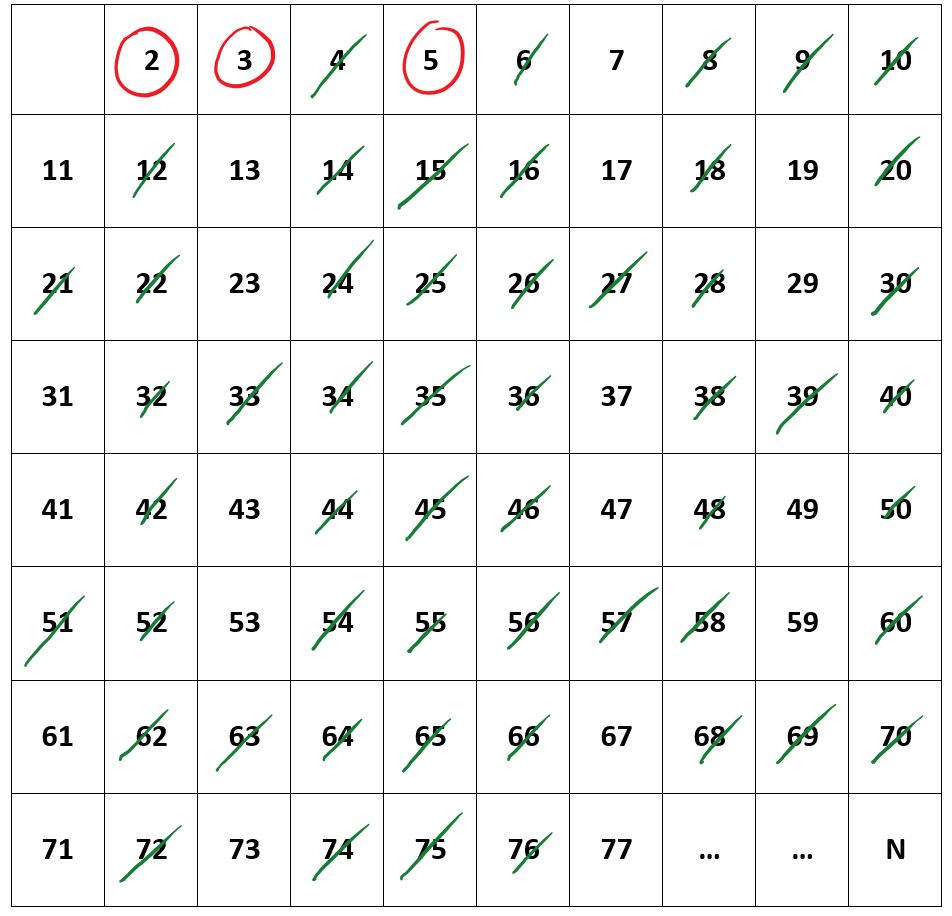
Beispiel
Laden
Idee des Verfahrens
Die Idee des Verfahrens ist es, die Liste auf die Primzahlen zu reduzieren. Die zusammengesetzten Zahlen fallen durch das Sieb und die Primzahlen bleiben zurück. Zusammengesetzte Zahlen bedeuten in diesem Zusammenhang, dass sich diese Zahlen in Primfaktoren zerlegen lassen.
Bislang gibt es keine Formel, mit der alle existierenden Primzahlen berechnet werden können. Das "Sieb des Eratosthenes" bietet zumindest die Möglichkeit, alle Primzahlen einer endlichen Liste systematisch zu bestimmen.
Vertiefende Aufgabe
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
