Primzahlen sind natürliche Zahlen größer als , die nur durch und sich selbst teilbar sind.
Es sind also genau die natürlichen Zahlen, die genau zwei Teiler besitzen.
So ist eine Primzahl, weil sie größer als ist und neben sich selbst und keine weiteren Teiler besitzt.
Die Zahl ist dagegen zusammengesetzt, also keine Primzahl, weil sie nicht nur und , sondern auch und als Teiler besitzt.
Primzahlen werden in der Praxis bei der Verschlüsselung von Daten gebraucht.
Primfaktorzerlegung
Zusammengesetzte Zahlen, also Nicht-Primzahlen größer als können in ein Produkt von kleineren Faktoren zerlegt werden. Zum Beispiel ist keine Primzahl, weil sie neben und auch den Teiler besitzt. Damit kannst du schreiben:
Die Zahl ist eine Primzahl und kann damit nicht weiter zerlegt werden. Demgegenüber ist keine Primzahl und kann weiter zerlegt werden. So ist ein Teiler von . Also kann weiter zerlegt werden:
Solange Nicht-Primzahlen im Produkt enthalten sind, kannst du es weiter zerlegen, bis nur noch Primzahlen im Produkt enthalten sind:
Wenn du eine natürliche Zahl größer als immer weiter in Produkte zerlegst, so erhältst du irgendwann ein Produkt, das nur Primzahlen enthält. Die besondere Eigenschaft der Primzahlen, dass sie nicht in Produkte mit kleineren Faktoren zerlegt werden können, sorgt dafür, dass am Ende ein Produkt mit ausschließlich Primzahlen entsteht.
Diese Zerlegung einer Zahl in ein Produkt aus Primzahlen wird Primfaktorzerlegung genannt.
Warum ist 1 keine Primzahl?
Die Multiplikation einer Zahl mit verändert diese Zahl nicht. Wenn du als Primzahl zulassen würdest, so könntest du eine Zahl immer weiter dadurch „zerlegen“, dass du als Faktor hinzufügst. Nimm die Zahl . Wäre eine Primzahl, so könntest du folgende unendliche „Primfaktorzerlegung“ durchführen:
Damit dies nicht geschieht, wird die nicht zu den Primzahlen gerechnet. Dadurch wird die Primfaktorzerlegung auch eindeutig.
Jede Primfaktorzerlegung einer Zahl ergibt immer dasselbe Ergebnis (wenn du die Faktoren in aufsteigende Reihenfolge bringst oder die Reihenfolge der Faktoren außer Acht lässt).
Die Primzahlen bis 99
Folgende Zahlen bis sind Primzahlen:
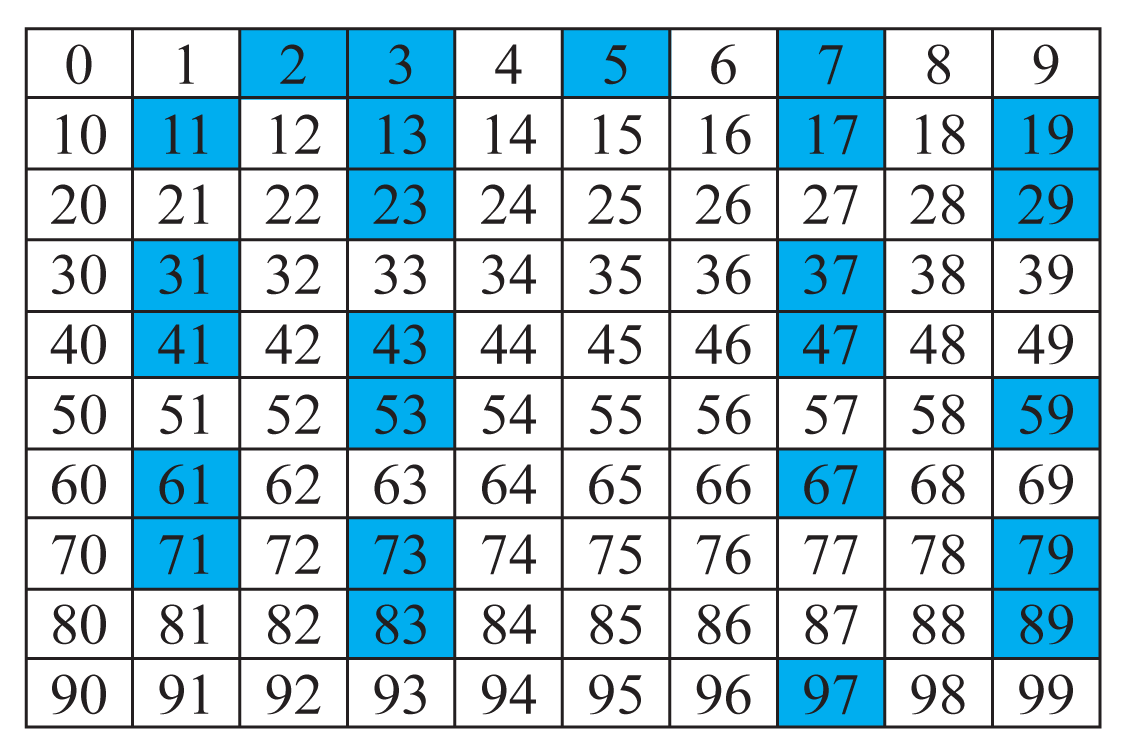
Überprüfen, ob eine Zahl eine Primzahl ist
Wenn du überprüfen möchtest, ob eine gegebene Zahl eine Primzahl ist, so besteht die einfachste Methode darin, zu versuchen, die Zahl der Reihe nach durch Primzahlen zu teilen.
Dabei helfen dir die Teilbarkeitsregeln. Wenn du einen Primteiler gefunden hast oder bei der Zahl selbst angekommen bist, hörst du auf. Für eine Zahl größer als heißt das:
Du testest, ob die Zahl durch teilbar ist. Wenn die Division ohne Rest aufgeht, hast du einen Teiler gefunden. Die Zahl ist keine Primzahl. Ist die Zahl jedoch nicht durch teilbar, so probierst du die nächste Primzahl als Teiler aus.
Du testest nun gegebenenfalls , , usw. als weitere Teiler.
Kann man auch früher aufhören?
Wenn du bis zur Wurzel der gegebenen Zahl alle Primzahlen als Teiler ausgeschlossen hast, dann ist die Zahl eine Primzahl. Andernfalls nicht.
Natürlich verwendet man aber heute mit Computern auch andere, effizientere Verfahren. Die Probedivision ist für sehr große Zahlen auch mit dem Computer praktisch undurchführbar.
Wie machst du dir bei großen Zahlen das Leben leichter?
Du musst zunächst nur untersuchen, ob eine Zahl durch eine Primzahl teilbar ist, auf das Ergebnis kommt es nur an, falls das der Fall ist. Die Teilbarkeit durch eine Zahl ändert sich nicht, wenn man Vielfache dieser Zahl addiert oder subtrahiert.
Es gibt unendlich viele Primzahlen
Die Anzahl der Primzahlen ist unendlich. Man kann also keine größte Primzahl finden. Es wird immer eine Primzahl geben, die größer ist. Den Beweis für diese Aussage hat Euklid schon vor mehr als Jahren geliefert.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Primfaktorzerlegung
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
