Aufgaben zur Prozentrechnung lassen sich auf unterschiedliche Weisen lösen. In diesem Artikel findet man die wichtigsten Formeln mit Erklärungen und Beispielen. Eine alternative Lösungsmethode ist das Lösungsverfahren mittels Dreisatz.
Für eine grundsätzliche Anschauung zum Prozentzeichen und seiner Bedeutung siehe Prozent. Hier werden auch die Fachbegriffe Grundwert, Prozentwert und Prozentsatz erklärt.
Eine detaillierte Einführung in all diese Begriffe gibt es in dem Kurs Einführung in Grundwert, Prozentwert und Prozentsatz.
Formeln für die Prozentrechnung
In den Formeln zur Prozentrechnung werden hier die folgenden Zeichen benutzt:
: Prozentwert : Grundwert : Prozentsatz
Um den Prozentwert, den Grundwert oder den Prozentsatz zu berechnen, braucht man sich nur eine Pyramide zu merken (in der Graphik kommt die gleiche Pyramide dreimal vor).
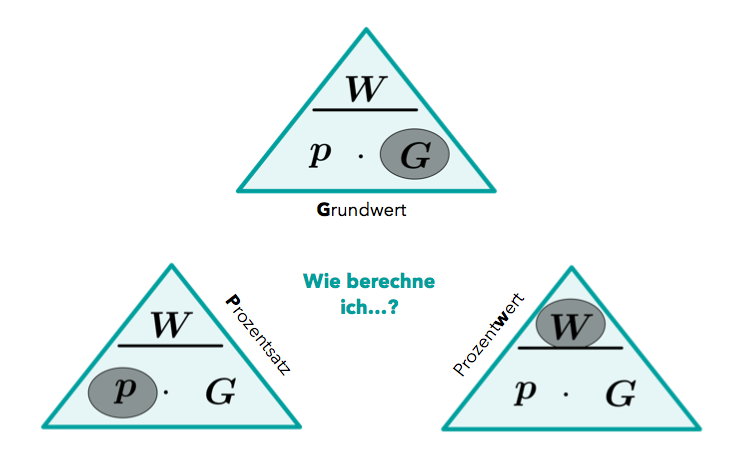
Sucht man zum Beispiel den Grundwert, so muss man ihn nur mit dem Finger zudecken (grauer Kreis in der oberen Pyramide). Übrig bleibt die Formel
(Der Strich unter dem bedeutet also eine Division.)
Genauso kann man den Prozentsatz oder den Prozentwert finden, indem man ihn in der Pyramide zudeckt.
Zusammengefasst lauten die Formeln:
Grundwert
Prozentsatz
Prozentwert
Bemerkung
Leider ist die Abkürzung für die drei Größen Prozentwert, Grundwert und Prozentsatz nicht immer gleich, es gibt viele alternative Bezeichnungen (z. B. Prozentwert oder – großgeschrieben zur Unterscheidung vom Prozentsatz , Grundwert , …).
Achtung
Wenn der Prozentsatz z. B. ist, dann ist und nicht .
Wenn der Prozentsatz z. B. ist, wird in manchen Schularten dieser Prozentsatz in die Formel eingesetzt, um zu erhalten.
Man kann diese Umrechnung auch bereits in den Formeln berücksichtigen und diese mit 100 % multiplizieren bzw. dividieren, um direkt die Prozentzahlen einsetzen zu können. Die %-Zeichen kürzen sich bei der Berechnung des Grund- oder des Prozentwerts, bei der Ermittlung des Prozentsatzes erhält man das Ergebnis gleich in der Prozentdarstellung.
Fragestellungen
Prozentwert | Grundwert | Prozentsatz | |
|---|---|---|---|
Beschreibung | Der Prozentwert gibt Antwort auf Fragen wie:
| Der Grundwert gibt Antwort auf Fragen wie:
| Der Prozentsatz gibt Antwort auf Fragen wie:
|
Beispiel | „Wie viel sind von Euro?“ | „Wenn Sie beim Kauf eines Autos € Rabatt bekommen haben und dies Rabatt auf den Kaufpreis entspricht, wie hoch war dann der Kaufpreis für das Auto?“ | „Wenn der Gewinn eines Unternehmens im Vorjahr € betrug und der Gewinn dieses Jahr bei € liegt, wie viel Prozent Gewinn hat das Unternehmen erwirtschaftet?“ |
Beispielaufgaben zur Prozentrechnung
Doch wie wendet man die Formeln zur Lösung von Aufgaben zur Prozentrechnung an? Folgende Beispiele erklären, wie man den Prozentwert, Grundwert oder Prozentsatz berechnet.
Hinweis: Der Artikel Prozentrechnung mittels Dreisatz löst die gleichen Aufgaben auf eine andere Art und Weise.
Prozentwert gesucht
Wie viel sind von ?
Einsetzen in die Prozentformel:
oder
Antwort:
von € sind €.
Grundwert gesucht
Eine Ware wurde um verbilligt und kostet jetzt €. Was kostete sie vorher?
Einsetzen in die Prozentformel:
Der Prozentwert gibt den Anteil am Grundwert an. Da die Ware um verbilligt wurde, kostet sie nur noch des Ausgangspreises, also des Grundwerts.
Antwort:
Sie kostete vorher €.
Prozentsatz gesucht
Von den Schülern haben zu Hause eine Katze. Wie viel Prozent der Klasse sind das?
Einsetzen in die Prozentformel:
Antwort:
Es sind .
Weiterführende Links
Mehr Informationen zum Thema „Rechnen mit Prozenten“ findest Du hier:
Weitere Aufgaben zum Thema „Rechnen mit Prozenten“ findest Du hier:
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
