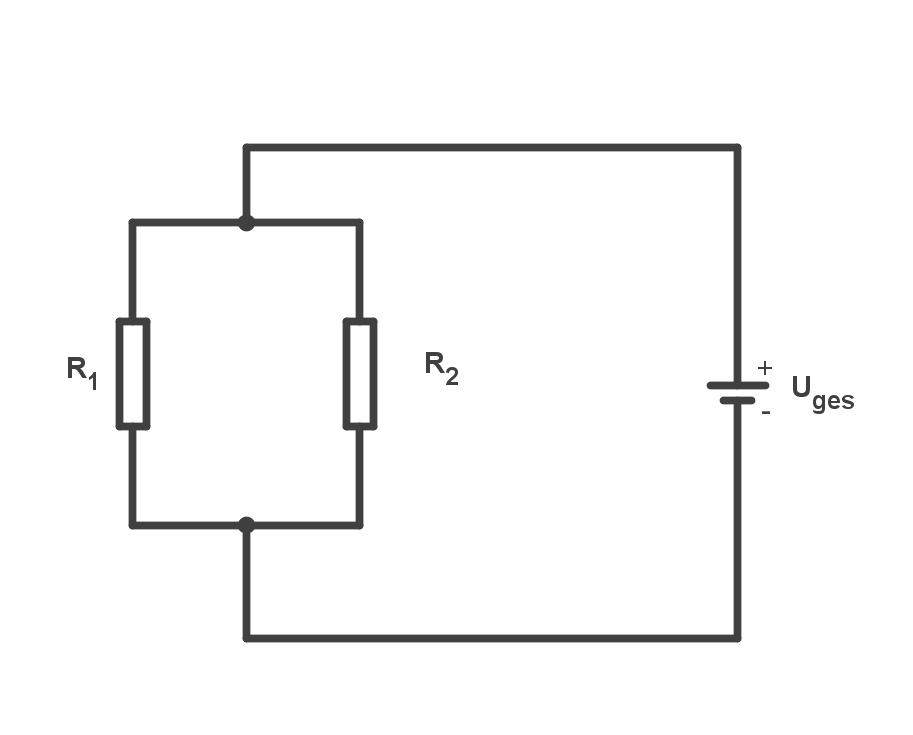
Bei der Parallelschaltung liegt eine Verzweigung vor, sodass die Bauteile sich auf verschiedenen Zweigen befinden, wie z. B, in der Abbildung rechts. Im Gegensatz zu der Reihenschaltung liegt hier überall die gleiche Spannung an.
Es gilt, dass der Gesamtstrom sich zu den einzelnen Strömen durch die Zweige 1, 2,… aufteilt:
In jedem Zweig fällt dieselbe Spannung ab, nämlich gerade soviel, wie die Spannungsquelle bereitstellt.
Der Gesamtwiderstand ist die Summe der Kehrwerte der einzelnen Widerstände der Zweige:
Erläuterung
Stromstärke
Die Stromstärke wird definiert als Ladungsfluss pro Zeit, . Durch die Verzweigung wird die Ladung geteilt, durch keinen Zweig fließt die Gesamtladung. bzw. . Zu beachten ist auch die Ladungserhaltung was
liefert. Durch Division mit erhält man die Beziehung für die Stromstärke und im allgemeinen Fall gilt dann:
Kirchhoff 1 liefert die gleiche Aussage. Die Summe der Stromstärken in den Zweigen vom Knotenpunkt weg ist gleich der Stromstärken zum Knotenpunkt hin.
Spannung
Die Spannung wurde als Arbeit pro Ladung definiert. Nun wird diese Arbeit von der Spannungsquelle verrichtet und wird benötigt, um den Widerstand zu überwinden. Alle Elektronen, sowohl die, die am Widerstand 1 als auch am Widerstand 2 ankommen, haben die gleiche Energie zur Verfügung. Damit ist die Energie, die ein Elektron an den Punkten A, B, und C besitzt, gleich. (Die Arbeit, die in den Leitungen benötigt wird, sei vernachlässigbar klein.)
Quantitative Betrachtung und Widerstand
Stromfluss durch die einzelnen Zweige
Teilt sich ein Stromkreis in mehrere Zweige mit ihren jeweiligen Widerständen auf, bestimmen diese Widerstände, wie sich die Stromstärke aufteilt. Gilt für jeden Widerstand das Ohmsche Gesetz
kann dieses zur Berechnung der Stromstärken zu umgestellt werden.
Der Strom durch den Widerstand im ersten Zweig ist demnach . Durch den Zweig 2 fließt die Stromstärke u.s.w.
Wenn zum Beispiel die Spannungsquelle in Abb. 1 eine Spannung erzeugt und die Widerstände , parallel geschaltet sind, dann ist der Stromfluss durch die jeweiligen Zweige
Die Berechnung Gesamtstromstärke verrät, wie Widerstände in der Parallelschaltung zu berücksichtigen sind.
Parallel geschaltete Ohm'sche Widerstände
Mit dem Ohmschen Gesetz und den Regeln für Strom und Spannung wurde im vorigen Abschnitt die Formel
gezeigt. Da die Spannung in jedem Zweig gleich ist, kann sie einfach ausgeklammert werden:
Wendet man das Ohmsche Gesetz nun auf den gesamten Stromkreis an, ist dieser Ausdruck aber nichts anderes als .
Vergleichen liefert eine Formel für den Gesamtwiderstand :
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
