In einer Reihenschaltung befinden sich die Bauteile aneinandergereiht, wie die Widerstände rechts in der Abbildung. Wichtig ist dabei, dass alle Bestandteile vom gleichen Strom durchflossen werden.
Der Stromfluss durch die Verbraucher 1, 2,… ist gerade der Gesamtstrom ,
Die Summe der Spannungen, die an den einzelnen Verbrauchern abfällt, ergibt die Gesamtspannung, die durch die Spannungsquelle erzeugt wird:
Die einzelnen Widerstände der Verbraucher summieren sich zum Gesamtwiderstand
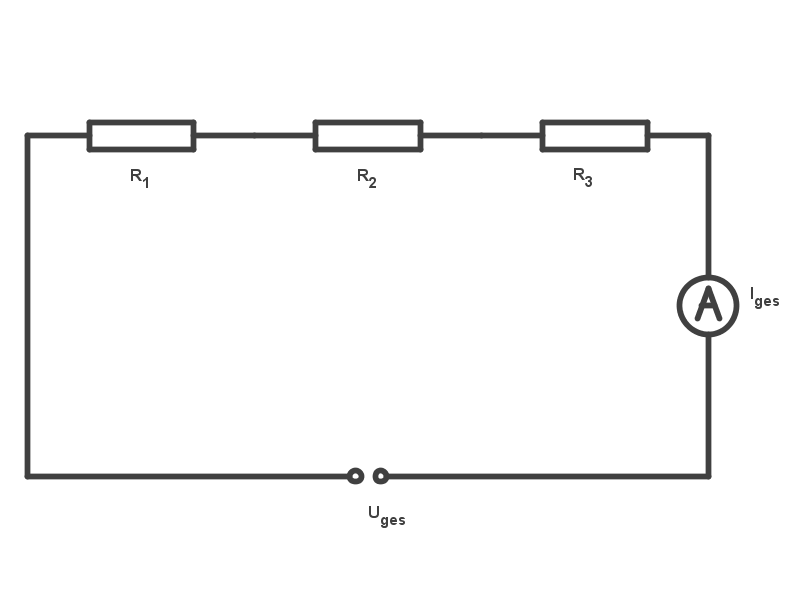
Erläuterungen
Dieser Stromkreis mit Ohm'schem Widerstand soll ein Beispiel für die obigen Formeln sein. Auch eine Glühlampe kann näherungsweise als Ohm'scher Widerstand betrachtet werden. Nur beim Ein- und Ausschaltvorgang gibt es größere Abweichungen.
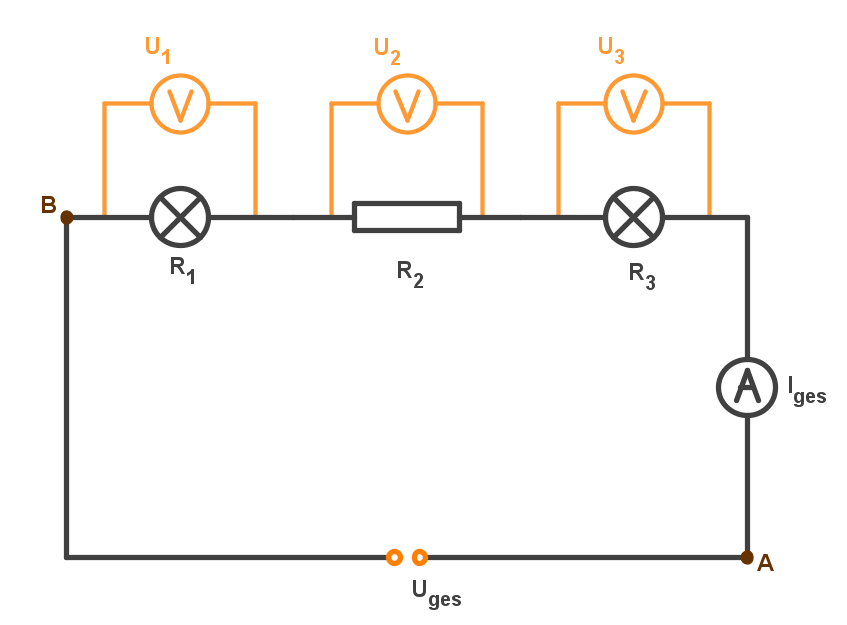
Stromstärke
Die Stromstärke einer Reihenschaltung bleibt überall gleich. Das erkennt man auch an der Definition der Stromstärke: . Die Menge an Ladung, die in einer bestimmten Zeit eine Stelle des Stromkreises passiert. Da auf dem Weg keine Ladungen entstehen oder verschwinden, wird die Anzahl der Ladungen, die in einer bestimmten Zeit z. B. Position A passieren, gleich sein wie bei B und genau so am Widerstand oder in den Glühlampen. Die Kirchhoff'sche Regel zeigt die gleiche Aussage. Zwischen den Positionen A und B befindet sich keine Verzweigung, also bleibt die Stromstärke gleich.
Widerstand
Zuerst wird der Stromkreis, mit nur einer Glühlampe, mit als Widerstand und der Spannung von aus der Quelle betrachtet. Nach dem Ohm'schen Gesetz gilt:
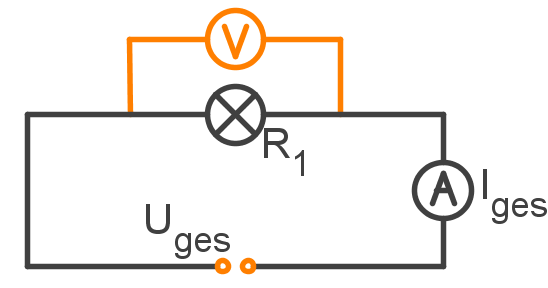
Nun wird der Widerstand mit eingebaut. Diesmal misst man die Stromstärke bei gleichbleibender Spannung und erhält . Nach einer Umstellung liefert das Gesetz,
Anscheinend haben sich die Widerstände addiert, denn
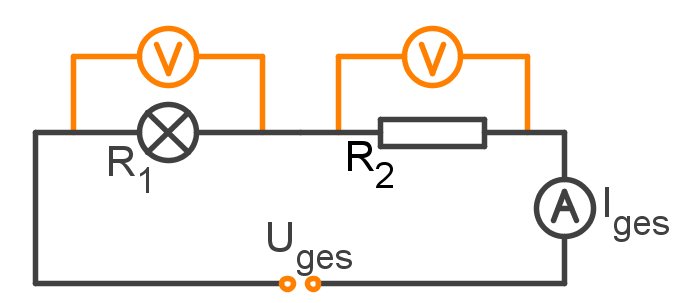
So ist auch die Regel für die in Reihe geschalteten Widerständen. Der Widerstand ist wie ein Hindernis für die Elektronen, wobei die Stromstärke die Flussmenge beschreibt und die Spannung den Antrieb, mit der diese Elektronen in Bewegung gesetzt werden. Wenn nun bei gleicher Spannung zwei Hindernisse aufeinander folgen, so wird der Stromfluss auch stärker beeinträchtigt. Der Gesamtwiderstand ist höher und setzt sich aus beiden Werten zusammen.
Um das Beispiel fortzusetzen, wird der Widerstand hinzugenommen, die zu erwartende Stromstärke berechnet. Als Gesamtwiderstand ergibt sich
Nach dem ohmschen Gesetz erhält man:
Spannung
Hier geht es um die Frage, welche Teilspannung an den einzelnen Widerständen anliegt. Die ist mithilfe der vorherigen Regeln leicht zu beantworten. Das Beispiel soll wieder der Stromkreis von oben mit den Widerstanden sein. Hier liegt bereits die Gesamtspannung von an. Die Stromstärke bleibt überall gleich und liegt bei
Die Summe der Teilspannungen ist also gleich der Gesamtspannung.
Damit ergibt sich für die einzelnen Bauelemente mithilfe des Ohmschen Gesetzes
Die gesamte Arbeit, die von der Spannungsquelle zum Transport der Ladungen verrichtet wird, setzt sich aus den Teilenergien an den Widerständen zusammen.
Allgemein gilt:
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
